Oeuvres complètes. Tome VIII. Correspondance 1676-1684

[p. 353]

N^o 2260.
L'Abbé de Catelan.
Appendice I au No. 2259.
[1681].

La pièce a été publiée dans le Journal des Sçavans¹⁾.

Remarque de Mr. l'Abbé de Catelan sur la proposition fondamentale de la iv. partie du Traitté de la Pendule de Mr. Hugens.

Monsieur Hugens ne voulant rien omettre dans son Traitté de la Pendule, qui eust rapport à cette matiere l'a divisé en quatre²⁾ parties dans la derniere³⁾ desquelles il examine fort au long la question du centre d'oscillation ou de balancement. Mais comme il est assez difficile que l'esprit soit toûjours également attentif à des veritez aussi abstraites que celles des Mathematiques, il ne faut pas s'estonner s'il n'a pas si bien reussi sur cette question que sur les autres⁴⁾ qu'il traitte dans le

1) Dans le numéro XXV, du Lundy 8 Sepembre m.dc.lxxxi, de l'édition d'Amsterdam. Consultez la note 4 de la Lettre N^o. 2259.
Le titre de l'édition d'Amsterdam est le suivant:
Journal des Scavans. De l'An m.dc.lxxxi. Par le Sr. A.D.L.R. Tome Neuvième. A Amsterdam, Chez Pierre Le Grand, m.dc.lxxxii.
L'écrit de l'abbé de Catelan a été imprimé pour la seconde fois dans l'édition d'Amsterdam, en tête de l'An m.dc.lxxxii. Ce volume a paru en 1683, c'est-à-dire plusieurs moisaprès que la critique de Huygens avait été publiée dans l'édition de Paris.
Ce premier article est précédé d'un avis: ‘L'imprimeur au Lecteur’, dans lequel on a reproduit, avec quelques modifications, l'avis qui précède l'année 1682 de l'édition de Paris, en y ajoutant ce qui suit:
‘On a imprimé parmy les journaux de l'année dernière 1681. une Remarque sur la 4. partie du Traité de la Pendule de Mr. Hugens, & un examen Mathematique du Centre d'Oscillation ou de balancement, qui sont de Mr. l'Abbé de Catelan. Comme la copie dont on s'est servy n'estoit pas correcte il se trouve qu'il y a plusieurs mots passez, & mesme des lignes entières omises. Un Amy qui a bien voulu nous avertir de ces fautes, nous ayant communiqué une coppie exacte de ces deux pièces, nous avons jugé à propos pour la commodité du Lecteur de les r'imprimer icy, puis qu'aussi bien, il en est parlé dans divers journaux de cette année.’ Nous donnons dans les notes les variantes de cette seconde impression, en omettant celles qui ne regardent que l'orthographe.
On verra que la phrase ajoutée de la note 8 a évidemment pour but de se soustraire après coup à la critique déjà publiée de Huygens, en introduisant un nouveau principe, ainsi que le remarque Chr. Huygens dans ses lettres à J.P. de la Roque, du 1^er avril 1683 et du 8 juin 1684.

2) L'édition de l'année 1682 a: cinq.

3) L'édition de l'année 1682 a: 4^e.

4) L'édition de l'année 1682 a: s'il n'a pas examiné cette question avec autant d'exactitude que les autres.

[p. 354]

mesme ouvrage. Voicy le Principe sur quoy roule tout son systeme du centre d'oscillation:

Si pendulum è pluribus ponderibus compositum atque è quiete dimissum, partem quamcunque oscillationis integrae confecerit, atque inde porrò intelligantur ponder a ejus singula, relictô communi vinculô, celeritates acquisitas sursum convertere, ac quò usque possunt ascendere; hoc factô centrum gravitatis ex omnibus compositae ad eandem altitudinem rever sum erit, quam ante inceptam oscillationem obtinebat. C'est à dire, si un pendule composè de plusieurs poids se brise dans son balancement ensorte que tous ces poids se réfléchissent⁵⁾ leur commun centre de pesanteur remonter a à la mesme hauteur d'où il estoit descendu.

Pour démonstrer que cette proposition n'est pas vraye il suffit de faire remarquer que la force qu'on nomme pesanteur, agit tout autrement dans les poids qui sont attachez ensemble que dans ceux qui sont séparez les uns des autres. Soyent A & B deux poids égaux dont il ne faut considerer icy ni la grosseur ni la figure comme s'ils estoient reduits chacun dans un point: si les ayant d'abord suspendus separement à un mesme point D, & élevez dans un mesme plan Horisontal DAB; on les laisse tomber d'eux mesmes jusqu'en F & G; leurs pesanteurs par une raison de mécanique conforme à l'experience & aux principes de la Physique s'augmenteront dans une telle proportion, ou ce qui est la mesme chose, ils acquierront des vitesses qui auront un tel rapport que leurs quarrez seront entre eux comme les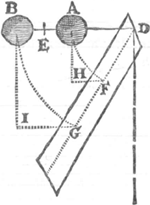



hauteurs AH & BI d'où ces poids descendront perpendiculairement à l'Horison. Que si ensuite l'on attache ces deux poids ensemble par une verge inflexible BA qu'on doit supposer sans pesanteur, & qu'aprés les avoir suspendus au mesme point D dans les mesmes distances DA, DB, on les laisse descendre en F & G de la mesme hauteur qu'auparavant, le Pendule qu'ils composeront acquierra autant de vitesse que la somme des deux Pendules simples, puisque le centre de pesanteurs commun E demeurera le mesme qu'il estoit⁶⁾; mais les parties dans lesquelles cette vitesse totale se partagera aux poids A & B seront entre elles comme les arcs AF, BG, ou les rayons DF, DG, parce qu'alors la proportion du mouvement de ces poids dépendra de leur situation à l'égard du point de suspension D qui en est le centre. Or les triangles HAF & IBG, comme aussi les

5) L'édition de l'année 1682 a: en sorte que tous ces poids se détachent les uns des autres & se réfléchissent.

6) La nouvelle édition de 1682 ajoute: & que les poids ne changeront point de situation à l'égard du centre de la Terre;

[p. 355]

triangles AFD & BGD, estant semblables, leur côtez AH & BI, AF & BG, DF & DG sont proportionels, c'est à dire, qu'il y a égalité de rapport entre les hauteurs d'où les poids A & B descendront, & entre les vitesses qu'ils acquierront en descendant. Mais les hauteurs sont les mesmes que dans la premiere supposition: Les vitesses sont donc differentes; puisque ces hauteurs estant proportionelles aux vitesses des poids lors qu'ils sont attachez ensemble, elles ne le sont qu'aux quarrez de leurs vitesses lors qu'ils sont separez. Supposé maintenant que le pendule composé des poids A & B rencontre dans son balancement quelque plan dur DFG contre lequel il se brise en sorte que ces poids se détachent l'un d'avec l'autre, ils seront réflechis par les tangentes des arcs FA & GB à des hauteurs qui seront entre elles comme les quarrez des vitesses qu'ils ont acquises en tombant, c'est à dire, comme les quarrez des rayons DF, & DG⁷⁾ car la separation de ces poids ne change point la quantité de leur mouvement; elle fait qu'ils se meuvent suivant la loy des corps pesants qui ne sont pas attachez ensemble. Il est demontré dans les Mécaniques que la hauteur perpendiculaire à l'Horison de laquelle descend ou à laquelle monte le centre de pesanteur commun à plusieurs poids est égale à la somme des hauteurs par rapport, ausquelles ces poids descendent ou montent divisée par leur nombre: Mais on vient de prouver que les poids qui se detacheroient d'un pendule rompu par le choq d'un plan opposé à son agitation remonteroient à des hauteurs differentes de celles d'où ils seroient descendus⁸⁾: Si l'on divise donc les differentes sommes des unes & des autres par le nombre de ces poids, l'on aura la hauteur à laquelle le centre de pesanteur commun remontera, différente de celle d'où il descendra, puisque ce sont des aliquotes pareilles de grandeurs inégales. La proposition de Mr. Hugens n'est donc pas vraye, ni par consequent tout ce qu'il en conclud touchant le centre d'Oscillation⁹⁾. On pourra donner dans la suite la véritable resolution Mathematique de cette Question.

7) La nouvelle édition ajoute: ou de leurs proportionelles AH & BI.

8) La nouvelle édition ajoute: & telles que les sommes de part & d'autre ne peuvent estre égales, car les dernieres de ces hauteurs ont toûjours pour racines des grandeurs qui sont proportionelles aux premieres & qui composent de plus la mesme somme que leurs racines laquelle exprime la vitesse totale du pendule AB.

9) La nouvelle édition fait suivre: Voicy la veritable resolution Mathématique de cette Question.