Oeuvres complètes. Tome VIII. Correspondance 1676-1684

[p. 349]

N^o 2259.
Christiaan Huygens à J.P. De la Roque.
16 avril 1682.

La minute se trouve à Leiden, coll. Huygens¹⁾.
Une partie de la lettre a été imprimée dans le Journal des Sçavans²⁾.
De la Roque y répondit par le No. 2262.

Pour Mr. l'Abbé la Roque.

envoié le 16 Avr. 1682.

Monsieur

La varietè et la nouveautè des choses contenues dans vos Journaux, qui fait que tout le monde les recherche, me les rend pour moy des livres defendus, lors que j'ay besoin de prendre garde au restablissement de ma santè, par ce que je crains d'y trouver nouvelle matiere d'estude et d'application. C'est qui est cause que je n'ay rien sceu de ce que vous y avez inseré contre moy de la part de M. l'Abbé de Catelan³⁾ du mois de Septembre dernier⁴⁾ jusques a ce que j'ay trouvé chez

1) Dans le livre F des Adversaria.

2) Du Lundy 29 Juin m.dc.lxxxii. La rédaction y a été modifiée en quelques endroits. Voir la pièce N^o. 2267. Consultez, sur les motifs de cette modification, la Lettre N^o. 2266.

3) L'abbé de Catelan, au sujet duquel nous n'avons trouvé aucun détail biographique, est connu par ses attaques contre les géomètres de son temps, dont il ne saisissait pas les démonstrations ou refusait de reconnaître les mérites dans l'invention de nouvelles méthodes de calcul.
Outre sa controverse avec Huygens, dont nous reproduisons tous les détails, il en a eu une avec le marquis De l'Hospital au sujet de l'ouvrage:
Logistique pour la Science generale des lignes courbes, ou maniere universelle & infinie d'exprimer & de comparer les puissances des grandeurs. A Paris chez Charles Roberstal. 1691. in-12^o, publié par de Catelan, sans nom d'auteur.
Cette dispute, commencée par des lettres publiques, fut continuée dans les numéros suivants du Journal des Sçavans de 1692;

4 février, analyse de l'écrit de Catelan par la rédaction;

21 avril, critique anonyme du marquis de l'Hospital;

18 août; mémoire touchant une methode pour les Tangentes des lignes courbes, etc. de de Catelan.

25 septembre, réponse à quelques objections contre son écrit, par de Catelan;

15 décembre, réplique de de l'Hospital, sous le pseudonyme de Mons. G***, à l'article du 18 août;

22 décembre, réplique, par le même, à l'article du 25 septembre.

Au sujet de l'ouvrage de l'Abbé de Catelan, Montucla dit (Histoire des Mathématiques, Tome II, p. 399):
‘Il y eut d'abord des géomètres qui, sans attaquer directement la nouvelle méthode (le calcu! infinitésemal), cherchèrent à en obscurcir le mérite; tel fut entr'autres l'abbé de Catelan, Cartésien zélé jusqu'à l'adoration, et qui s'étoit déjà signalé par une mauvaise querelle, intentée à Huygens, au sujet de sa théorie du centre d'oscillation. Cet abbé donna en 1692 un livre intitulé Logistique universelle, & Méthode pour les tangentes, &c. Il y disoit dans un petit avertissement, que cet essai étoit propre à montrer qu'il valoit mieux s'attacher à pousser plus loin les principes de M. Descartes sur la Géométrie, qu'à chercher de nouvelles méthodes. Mais on ne peut guère se refuser à une sorte d'indignation, quand on voit que tout ce Traité n'est que le calcul différentiel déguisé mal-adroitement sous une notation moins commode et moins avantageuse. Aussi cet auteur ne marche-t-il qu'à travers des embarras sans nombre, et ce qui, traité suivant la méthode du calcul différentiel, est clair et ne demande que quelques lignes, suivant la sienne est obscur, embrouillé et occupe des pages entières. D'ailleurs le livre n'est pas sans erreurs, et M. le marquis de l'Hôpital vengea le calcul differentiel, en les relevant; ce qui excita une querelle, dont retentit à diverses reprises le Journal des Savans, de 1692.’

4) Voir l'Appendice I, N^o. 2260. Cet écrit n'avait pas été publié dans le Journal des Sçavans, édition de Paris. On verra par la suite que quelque malintentionné envers Huygens, trèsprobablement Hartsoeker (voir la Lettre N^o. 2264), avait trouvé moyen de le faire insérer dans l'édition d'Amsterdam, contresaçon de celle de Paris, à la place d'autres articles de l'édition de Paris.

[p. 350]

nos libraires les journaux de l'annee passée imprimez ensemble en ce pais. J'ay estè surpris de voir qu'il ait attaquè ma theorie des centres de Balancement ou personne depuis 9 ans qu'elle a estè publiée dans mon traitè des Pendules n'avoit rien trouvè a dire mais ayant examinè sa pretendue refutation de mon theoreme je l'ay trouvee telle que je m'estonne que depuis 7 mois qu'elle est imprimée, l'autheur luy mesme ne se soit point avisè de retracter. Car pour vous dire en peu de mots quelle est sa bevue, c'est qu'il veut que s'il y a deux lignes et encore deux autres de differente proportion que les premieres il veut, disje, que la somme des deux dernieres, ne puisse estre egale a la somme des deux premieres. Figurez vous les deux premieres de 4 et 8 pieds et les deux autres de 3 et de 9, et voyez si la somme des unes aussi bien que des autres ne peut pas estre 12⁵⁾.

Pour vous faire entendre que son erreur revient precisement a cela je me serviray du mesme exemple qu'il propose. A et B sont deux poids attachez à une verge ou ligne DB, qu'il faut considerer comme sans pesanteur et inflexible, et qui puisse tourner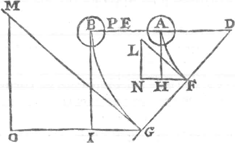



librement sur le point D. C'est icy ce que j'appelle un pendule composè des poids AB. Et leur centre d'oscillation est le point P lorsque la distance PD est egale a un pendule simple qui fait des balancemens de mesme duree que le pendule composè D A B. Or je dis, que si ce pendule fait une partie de son balancement, par exemple jusqu'en DFG, et que rencontrant là quelque plan contre le quel il se brise, les 2 poids se detachent de la ligne inflexible, et qu'ils tendent chacun avec sa vistesse acquise vers en haut jusqu'ou ils peuvent, comme en L et M, rou-

5) Au-dessus des nombres 4, 8, 3, 9, 12, Huygens a écrit dans la minute: 5, 10, 3, 12, 15. Comparez la Lettre N^o. 2265.

[p. 351]

lants si l'on veut par les plans inclinez qui touchent les arcs AF, BG. Je dis donc que le centre de pesanteur commun des corps A, B, montez en L et M, sera a mesme hauteur qu'il estoit en E, devant que le balancement fust commencè.

Mr. l'Abbé de Castelan pour prouver la fausseté de cette proposition, demontre que les hauteurs ou les 2 poids detachez sont montez comme icy NL, et OM sont differentes de celles d'ou ils sont descendus a scavoir AH, BI. Ce qui est tres vray par la raison qu'il donne que les unes sont entre elles comme les quarrez de DF, DG, et les autres comme ces mesmes lignes. Si l'on divise donc, dit il, les differentes sommes des unes et des autres par le nombre de ces poids, (c'est a dire si l'on prend la moitié des lignes LN, MO, et puis la moitié des lignes AH, BI) l'on aura d'un costè la hauteur, dont le centre de pesanteur commun est remontè, et de l'autre la hauteur dont ce centre est descendu. Il est encore vray que par cette division l'on aura ces deux hauteurs mais je ne demeure pas d'accord que les sommes a diviser fussent differentes, et c'est ce que Mr. l'abbé ne pourra pas prouver ni par consequent que les deux hauteurs trouvees du centre de gravité soient inegales ainsi qu'il pretend dans sa conclusion. Car encore que les hauteurs LN et MO soient de proportion chacune differente d'avec AH et BI, il ne s'en suit pas que la somme des unes et des autres ne soit la mesme. Et cette meprise est si grossiere que je ne scay pas comment il est possible qu'on y puisse tomber.

Je pourrois remarquer outre cecy un autre endroit encore ou Mr. l'abbé s'abuse grandement, mais je ne m'y arresteray pas, par ce que ce qu'il y avance n'entre point dans ce qu'il apporte contre moy. Je diray seulement encore un mot touchant son Examen Mathematique du centre d'oscillation que vous rapportez dans le Journal du 15 dec.⁶⁾ ou il pretend par son raisonnement avoir trouvè cette regle generale qui est

Qu'il faut diviser par le nombre des parties d'un pendule la somme des racines de leurs distances de l'axe pour avoir une ligne droite qui soit la mesure du temps du balancement de ce pendule de la quelle par consequent le quarrè ou la troisieme proportionnelle sera la distance d'entre l'axe et le centre d'oscillation.

Sans examiner autrement cette regle il suffit pour en faire voir la faussetè de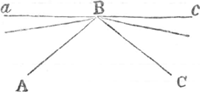



remarquer que suivant elle le centre d'oscillation de deux lignes pesantes comme AB, BC attachees ensemble en quelque angle que ce soit et suspendues en B auroient tousjours un mesme centre d'oscillation, et par consequent les balancemens egalement vistes comme il est aisè de comprendre a ceux qui entendent tant soit peu cette matiere. Mais ils verront aussi que cette egalitè de balancement ne scauroit avoir lieu, par

6) Cette pièce non plus n'avait pas paru dans l'édition de Paris. Consultez la Lettre N^o. 2262, note 2.

[p. 352]

ce qu'a la fin les 2 lignes estant jointes en une ligne droite aBc, elles devroient faire les balancements dans les mesmes temps qu'estant jointes en ABC, au lieu que la ligne droite ne fait point de balancemens estant suspendue par son milieu ou qu'elle les fait pour ainsi dire d'une lenteur infinie. Je crois au reste que Mr. l'abbé de Catelan auroit bien de la peine a determiner par sa regle le centre de balancement dans les figures particulieres mesmes les plus simples, mais s'il en peut venir a bout dans quelques unes, il trouvera que jamais sa Theorie ne s'accordera avec l'experience et que la miene y conviendra tousjours dans la derniere precision, pourvu que l'experience soit faite sans erreur. A propos de quoy je nè puis omettre de vous dire que le Pere Deschales⁶⁾ quelque part dans son grand Cours de Mathematique, en raportant une experience qu'il a faite d'un pendule composè de deux poids, sans mettre en compte comme il devoit la pesanteur du baston ou ils estoient attachez, accuse a tort les regles que j'ay donnees pour le centre de balancement de ce qu'elles ne respondent pas à ce qu'il a trouvè en effect. Si les poids A, B, sont egaux et aussi les distances DA, AB. par ex. chacune d'un pied la distance entre le centre de balancement et le point D selon ma regle sera de 20 pouces et selon celle de M. l'abbé cette distance sera moindre que de 17 pouces 7 lignes⁷⁾.

Je m'assure Monsieur que vous voudriez bien avoir la bontè de mettre dans vostre Journal ce que je viens d'escrire jusqu'icy, afin que ceux qui n'ont pas lu mes demonstrations ou qui ne les ont examinees que legerement ne croyent pas que les remarques de Mr. l'abbé de Catelan soient quelque chose de fort considerable pour estre debitees avec beaucoup d'assurance. Que s'il s'avise peut estre d'escrire une replique a ce que dessus, vous m'obligerez si devant que de les publier pour luy vous faites en sorte qu'il la communique a quelque personne de scavoir. Cela importe mesme à son honneur. Et a vous dire la veritè il m'est bien fascheux de me voir attaquè par de gens si ignorants et d'estre obligè de respondre a leur objections par ce que par le moyen de vos journaux elles sont vues par toute l'Europe, et semblent devoir estre quelque chose. Je vous prie donc de me menager un peu d'avantage a l'avenir en ne donnant pas si facilement place dans vos Escris a tous ceux qui voudroient me donner de pareil exercice. Je demeureray toute ma vie &c.

6) Sur Claude François Milliet Deschales et son ‘Cursus seu Mundus mathematicus’, consultez la Lettre N^o. 1402, notes 1 et 4.

7) Deschales a plus tard reconnu son erreur. Il s'est rétracté dans la dix-septième proposition du livre quatrième de son ouvrage:
Traitté du Mouvement et du Ressort, par le R.P.C.F.M. De Chales de la Compagnie de Jésus, Lyon, 1682, in-8^o.