Oeuvres complètes. Tome VIII. Correspondance 1676-1684

[p. 368]

N^o 2267.
Christiaan Huygens à J.P. De la Roque.
1682.
Appendice I au No. 2266.

La piéce a été imprimée dans le Journal des Sçavans¹⁾.

Extrait d'une Lettre de Mr. Hugens avec sa réponse à une remarque faite par Mr. l'Abbé de Catelan contre sa proposition 4 du Traité des centres de Balancement.

J'ay esté surpris de voir qu'on ait attaqué ma Theorie du centre de Balancement, où personne depuis neuf ans qu'elle est imprimée n'avoit trouvé rien à [re] dire: mais ayant consideré la [] refutation [que] Mr. l'Abbé de Catelan [fait] de ma 4. proprosition, [je n'ay pas apprehendé] qu'elle me fist tort dans le monde. Car pour vous dire en peu de mots [en quoy il se trompe], c'est qu'il veut que s'il y a deux lignes, & encore deux autres de differente proportion que les premieres, [] la somme des deux dernieres ne puisse estre égale à la somme des deux premieres.

Figurez vous les premieres de 5. & de 10. pieds, & les autres de 3. & de 12. & voyez si la somme des unes aussi bien que des autres ne peut pas estre 15²⁾. Pour vous faire entendre que son erreur revient precisément à cela, je me serviray du mesme exemple qu'il propose.

A & B sont deux poids attachez à une verge ou ligne DB, qu'il faut considerer comme inflexible, & sans pesanteur, & qui puisse tourner librement sur le point D. [C'est là ce que j'appelle un pendule composé des poids A, B. & je dis] que si ce



pendule fait une partie de son balancement, par exemple jusqu'en DFG, & que rencontrant là quelque plan contre lequel il se brise, les deux poids se detachent de la ligne inflexible, & qu'ils tendent chacun avec sa vitesse acquise vers en haut, montant jusqu'ou ils peuvent, comme en L & M [sur des plans inclinez si l'on veut, qui

1) Du Lundy 29 Juin, m.dc.lxxxii, édition de Paris. Elle y est précédée d'un préambule de l'éditeur, de la Roque; voir l'Appendice II, N^o. 2268.
L'édition d'Amsterdam a reproduit l'article de Chr. Huygens, en omettant, bien entendu, les remarques préliminaires de de la Roque.
Nous plaçons entre crochets les passages de l'imprimé que s'écartent de la rédaction primitive de Chr. Huygens, dans ses Lettres N^os. 2259 et 2266.

2) Voir, pour ces chiffres, la Lettre N^o. 2259, note 5.

[p. 369]

touchent les Arcs AF, BG]. Je dis donc que le centre de pesanteur commun des [poids] A, B, montez en L, M, sera à mesme hauteur qu'il estoit en E, devant que le balancement fût commencé.

Mr. l'Abbé de Catelan pour prouver la fausseté de cette proposition démontre que les hauteurs où les deux poids détachez sont montez, comme icy NL, OM, sont differentes de celles d'où ils sont descendus sçavoir AH, BI. ce qui est tres vray par la raison qu'il donne, que les unes sont entr'elles [comme les lignes DF, DG, & les autres comme les quarrez de ces lignes]. Si l'on divise donc, dit-il, les differentes sommes des unes & des autres par le nombre de ces poids, c'est à dire, si l'on prend la moitié des lignes LN, MO, & puis la moitié des lignes, AH, BI; l'on aura d'un costé la hauteur dont le centre commun de pesanteur est remonté, & de l'autre la hauteur dont ce centre est descendu. Il est encore vray que par cette division l'on aura ces deux hauteurs; mais je ne demeure pas d'accord que les deux sommes à diviser fussent differentes; & c'est ce que Mr. l'Abbé [de Catelan] ne pourra pas prouver, ny par consequent que les deux hauteurs trouvées du centre de gravité soient inégales, ainsi qu'il pretend dans sa conclusion: car [bien] que les hauteurs LN, MO soient de proportion [] differente [entre elles] d'avec [les hauteurs] AH, BI, il ne s'ensuit pas que la somme des unes & des autres ne soit la même. []

Je pourrois remarquer outre cecy encore un autre endroit où Monsieur l'Abbé de Catelan [se trompe]; mais je ne m'y arresteray pas, parce que ce qu'il y avance n'entre point dans ce qu'il rapporte contre moy. Je diray seulement encore un mot touchant son examen Mathematique, [comme il l'appelle du centre d'osciltion qui est rapporté] dans le Journal du 15 Decemb. 1681. où il pretend par lon raisonnement avoir trouvé cette regle generale, [sçavoir] qu'il faut diviser par le nombre des parties d'un pendule la somme des racines de leurs distances de l'axe, pour avoir une ligne droite qui soit la mesure du balancement de ce pendule, de laquelle par consequent le quarré ou la troisième proportionelle sera la distance d'entre l'axe & le centre d'oscillation.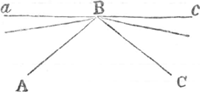

Sans examiner autrement cette regle, il suffit pour en faire voir la fausseté, que suivant [ce principe] le centre de balancement de deux lignes pesantes, comme AB, BC, attachées ensemble en quelque angle que ce soit & suspenduës en B, auroient toûjours un mesme centre d'oscillation, & par consequent les balancemens également vistes, comme [verront aisément] ceux qui entendent tant soit peu cette matiere. Mais ils verront aussi que cette égalité de balancemens ne scauroit avoir lieu; parce qu'à la fin les deux lignes estant jointes en une ligne droite a Bc, elles [auroient encore] les balancemens [de la mesme vitesse] qu'estant jointes en ABC; au lieu que la ligne

[p. 370]

droite ne fait point de balancemens estant suspenduë par son milieu, ou qu'elle les fait pour ainsi dire, d'une lenteur infinie.

Je crois au reste que Mr. l'Abbé de Catelan auroit bien de la peine à déterminer par sa regle le centre de balancement dans quelques figures particulieres mesme [des] plus simples; mais s'il en peut venir à bout, il trouvera que jamais sa Theorie ne s'accordera avec l'experience, & que la mienne y conviendra toûjours dans la derniere precision, pourveu que l'experience soit faite sans erreur.

[Je ne puis omettre à cette occasion de vous marquer] que le P. de Chales [dans quelque endroit] de son grand Cours Mathematique en rapportant une experience qu'il a faite d'un pendule composé de deux poids, sans mettre en compte, comme il devoit, la pesanteur du bâton où il les avoit attachez, accuse à tort les regles que j'ay données pour le centre de balancement, de ce qu'elles ne répondent pas à ce qu'il a trouvé en effet [].