Oeuvres complètes. Tome IX. Correspondance 1685-1690

[p. 457]

N^o 2605.
Le Marquis de l'Hospital à Christiaan Huygens.
19 Juillet 1690.
Appendice I au No. 2604¹⁾.

La pièce a été publiée dans l'Histoire des Ouvrages des Sçavans²⁾.

Lettre de Mr. le Marquis de l'Hospital à Monsieur Huygens, dans laquelle il pretend demonstrer la regle de cet Auteur touchant le centre d'Oscillation du pendule composé, par sa cause physique, & répondre en même temps à Mr. Bernoulli.

Il y a quelques années, Monsieur, que j'ay leu avec admiration vostre sçavant Traité des centres d'Oscillations, & que j'ay esté pleinement convaincu de la verité de vos demonstrations. Cependant les Journaux de Leipsic m'estant tombez depuis peu entre les mains, j'ay trouvé dans celuy du mois de Juillet de l'année 1686. le recit du differend que vous avez eu sur ce sujet avec Mr. l'Abbé Catelan, rapporté par Mr. Bernoulli³⁾ qui decide en vostre faveur, comme doivent faire assurément tous ceux qui pretendent tenir quelque rang parmi les Geometres. Mais j'ay esté fort surpris de voir que la fin de son raisonnement se trouve contraire



à vos demonstrations. Ce qui m'a donné lieu de l'examiner avec soin; & j'ay reconnu qu'il se sert d'un principe très-veritable, quoy qu'il se trompe dans l'application qu'il en fait. Car ce principe conduit, comme je vais montrer, à la même verité que vous avez prouvée dans vostre proposition V⁴⁾.

Soit la verge DAB inflexible, & sans pesanteur, mobile autour du point fixe D, dans laquelle soient enfilez les deux poids égaux A & B, & soit la distance BD au point fixe, quadruple de AD, l'on demande la longueur DG du pendule simple

1) La pièce accompagnait la lettre de l'Hospital du 19 juillet, notre N^o. 2600.

2) Dans la livraison du mois de juin, juillet & aoust, 1690, p. 440. Une traduction latine a été donnée par 's Gravesande dans: Christiani Hugenii etc. Opera Varia, Vol. I, p. 242.

3) Voir la pièce N^o. 2426.

4) Voir la pièce N^o. 2581, note 2.

[p. 458]

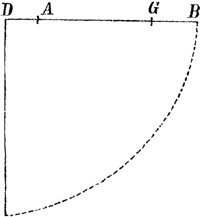
isochrone, c'est-à-dire qui se meuve avec la même vitesse que le pendule composé.

Pour resoudre ce probleme, je considere les vitesses avec lesquelles les corps A & B commencent à descendre dans le premier instant de leur chûte, ou si l'on aime mieux, les espaces qu'ils parcourent 'dans un même temps, quelque petit qu'on le prenne: & c'est dans ce sens que je mets 1 pour la vitesse avec laquelle tout corps pesant grand ou petit commence à descendre sur des plans également inclinez. Car, comme l'on sçait assez, cette vitesse est égale dans tous les corps. Je conçois aussi, que la quantité de mouvement d'un corps au commencement de sa descente, naist de sa masse multipliée par cette premiere vitesse. Cecy supposé, il est constant que le corps A tend à descendre avec la même vitesse que le corps B, & que ne le pouvant, parce qu'il est attaché en A, dont la vitesse n'est que la quatrième partie de celle de B, il doit haster le mouvement du corps B dans le pendule composé; & toute la difficulté consiste à determiner au juste de combien ce mouvement doit estre augmenté: & c'est ce que je fais en cette forte.

Soit x la quantité de mouvement du corps A dans le pendule composé, l'excès restant de sa quantité de mouvement sera donc A - x, qui estant appliqué en A, fait effort sur le point fixe D, & sur le corps B, que l'on doit envisager comme estant immobile à son égard (puis qu'il est evident que le corps B doit estre censé sans mouvement par rapport à cet excès) & par consequent la verge BD doit estre regardée comme un levier appuyé par les deux bouts en B & D. L'on aura donc BD, 4 est à AD, 1 comme A - x est à ¼ A - ¼ x portion de l'excès de la quantité de mouvement du corps A qui se distribüe en B: de sorte que la quantité de mouvement du corps B dans le pendule composé, sera B + ¼ A - ¼ x c'est-à-dire 5/4 A - ¼ x. Or à cause de la verge inflexible DB, la vitesse du corps B dans le pendule composé doit necessairement estre quadruple de celle du corps A, & par consequent aussi sa quantité de mouvement, puis que ces corps sont égaux: d'où il suit qu'il y aura égalité entre 4 x, & ⅘ A - ¼ x, d'où l'on tire une valeur x = 5/17 A, qui exprime la quantité de mouvement du corps A dans le pendule composé. Maintenant si l'on fait comme 5/17 vitesse du corps A dans le pendule composé est à 1 vitesse de tous les corps pesants au bout des pendules simples: de même DA, 1 est à DG, 17/5, ce sera la longueur du pendule simple isochrone; car les espaces estant entre eux comme les vitesses, le temps doit estre égal.

Si l'on ajoûte au pendule composé DAB le nouveau poids C égal à chacun des poids A & B, en sorte que DC soit double de DA, l'on doit considerer les poids A & B comme estant attachez en G leur centre d'oscillation, au bout du pendule simple DG: & alors mettant x pour la quantité de mouvement du corps C dans le pendule composé DCG, l'on aura C - x pour l'excès restant de la quantité de mouvement du corps C, qui estant appliqué en C, fait effort sur le point fixe D, & sur le point G, que je regarde

[p. 459]

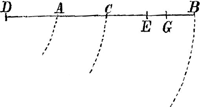comme estant sixe à son égard. L'on aura donc DG, 17/5 est à DC, 2 comme C - x est à 10C - 10 x / 17 portion de cet excès qui se distribüe en G: d'ou il suit que la quantité de mouvement des corps A & B dans le pendule composé DACB, sera 5/17 A + 20/17B + 10C - 10x / 17 c'est-a-dire 35C - 10x / 17. Or à cause de la verge inflexible DB, la vitesse du corps A dans le pendule composé sera necessairement la moitié de celle du corps C, & celle du corps B sera double de celle du corps C; & de même aussi leurs quantitez de mouvement, ces trois corps estant egaux. Il y aura donc egalité entre 2 x + ½ x, & 35C - 10x / 17, d'où l'on tire une valeur x = ⅔ C, qui exprime la quantité de mouvement du corps C dans le pendule composé DACB. Maintenant si l'on fait comme ⅔ vitesse du corps C dans le pendule composé, est à 1. vitesse de tout corps pesant au bout d'un pendule simple de même DC, 2 est à DE, 3, ce sera la longueur du pendule simple isochrone⁵⁾. Si les poids A, B, C, étoient inégaux, l'on trouveroit toûjours, en suivant ce raisonnement, le centre d'Oscillation, de sorte que cette methode est generale, quelque soit le nombre des poids, & quelque inégalité qu'ils ayent entre eux. Il faut maintenant faire voir qu'elle sert aussi, lors que les poids se trouvent de part & d'autre du point fixe.

Soit le pendule composé ADB mobile autour du point fixe D, & chargé des deux poids égaux A & B, & soit DB quadruple de DA, il est visible que le corps A doit retarder le mouvement du corps B dans le pendule composé; & pour trouver precisément de combien, je nomme x la quantité de mouvement du corps B dans le pendule composé ADB: & par consequent l'excès restant de sa quantité de mouvement sera B - x. Or à cause de la verge AB, la vitesse du corps A doit necessairement estre la quatriéme partie de celle du corps B. Donc sa quantité de mouvement dans le pendule composé sera ¼ x (car les corps A & B estant égaux, les quantitez de mouvemens sont proportionées aux vitesses).

Or cette quantité de mouvement ne peut avoir esté produite que par l'excès restant de celle du corps B. Il est donc evident que cet excès B - x doit vaincre la quantité de mouvement du corps A vers le bas, & luy en imprimer de plus ¼ x vers le haut; c'est-à-dire qu'il doit agir sur le corps A, comme si la force A + ¼ x estant appliquée immediatement en A, le poussoit vers le haut. Mais la force B - x, à cause

5) Résultat exact, puisque 1² + 2² + 4² / 1 + 2 + 4 = 3.

[p. 460]

du point fixe D, agit sur le corps A, comme si la force 4 B - 4x étant appliquée immediatement en A, poussoit ce corps vers le haut. Il y aura donc égalité entre 4B - 4x, & A + ¼x: d'où l'on tire une valeur x = 12/17B, qui exprime au juste la quantité de mouvement du corps B dans le pendule composé ADB. Maintenant si l'on fait comme 12/17 vitesse du corps B dans le pendule composé est à 1 vitesse de tout corps pesant au bout d'un pendule simple: de même DB, 4 est à DG, 17/3 ce sera la longueur du pendule simple isochrone.

Il est aisé de conclurre de tout cecy, que le principe de Mr. Bernoulli est veritable, & qu'il se trompe dans la conclusion qu'il en tire: parce qu'il considere les vitesses acquises des corps A & B, au lieu de considerer, comme nous avons fait, leurs vitesses commençantes, & de plus leurs quantitez de mouvemens. Car sans cela, on ne pourroit point appliquer ce principe, qui n'est autre que celuy du levier, lors que les corps sont inégaux. De sorte que je croy avoir pleinement satisfait à sa demande, Rogantur hac occasione eruditi, &c.

Vous voyez, Monsieur, comme differentes routes conduisent à la connoissance de la même verité. Ce n'est pas que je veuille comparer celle-cy à la vostre, qui est incomparablement plus sçavante & plus geometrique. Si vous jugez cependant qu'il ne soit pas inutile de faire voir, que les raisons physiques que j'apporte icy s'accordent parfaitement avec vos demonstrations, & qu'elles soient propres à lever le doute de Mr. Bernoulli, je consens que vous rendiez publique cette Lettre, & je vous prie de vouloir y ajoûter vos remarques⁶⁾, vous protestant que je n'appelleray point du jugement que vous porterez, qui ne peut estre que très-éclairé & très-équitable. Je suis très-parfaitement, &c.

6) Voir la pièce suivante N^o. 2606.