Oeuvres complètes. Tome IX. Correspondance 1685-1690

[p. 403]

N^o 2581.
Le Marquis de l'Hospital à Christiaan Huygens.
Appendice au No. 2580.
18 avril 1690.

La pièce se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek¹⁾.

Extrait d'une lettre de Mr. le Marquis de l'Hospital, Contenant vne demonstration Physique et naturelle de la Regle de Mr. Huguens touchant les Centres d'oscillation.

Le celebre Probléme du centre d'oscillation, a fait tant de bruit depuis quelques années, que presque tous les habiles Geometres s'y sont appliquez auec soin, L'illustre Mr. Huguens semble auoir épuisé cette matiere, dans le scauant traitté qu'il a composé sur ce sujet, jl nous y donne une Regle generale²⁾ pour trouuer le centre d'oscillation du pendule composé, qui sert de base et de fondement a tout le reste de son traitté; mais comme elle n'est qu'une suite de la prop. 4^e3), qui n'est demonstrée que par l'hypothese qu'il supose dès le commencement⁴⁾, et qui ne paroist pas assés simple, ni assés euidente pour estre ainsy suposée sans preuve, cela a donné lieu à plusieurs contestations. Entr'autres Mr. l'abbé Catelan y a fait des objections⁵⁾, ausquelles Mr. Huguens a répondu⁶⁾ et en dernier lieu Mr. Bernoully, dans les journaux de Lipsic de l'année 1686. pag. 356⁷⁾, y a satisfait plei-

1) Voir, à la page 216, l'ouvrage cité dans la Lettre N^o. 2580, note 2.

2) Dans la Prop. V de la Pars Quarta: Dato pendulo ex ponderibus quotlibet composito, si singula ducantur in quadrata distantiarum suarum ab axe oscillationis, & summa productorum dividatur per id quod sit ducendo ponderum summam, in distantiam centri gravitatis communis omnium ab eodem axe oscillationis; orietur longitudo penduli simplicis composito isochroni, sive distantia inter axem & centrum oscillationis ipsius penduli compositi.’

3) ‘Si pendulum è pluribus ponderibus compositum, atque è quiete dimisium, partem quamcunque oscillationis integrae confecerit, atque inde porro intelligantur pondera ejus singula, relicto communi vinculo, celeritates acquisitas sursum convertere, ac quousque possunt ascendere; hoc facto, centrum gravitatis ex omnibus compositae, ad eandem altitudinem reversum erit, quam ante inceptam oscillationem obtinebat.’

4) Il s'agit de l'hypothèse I: ‘Si pondera quotlibet, vi gravitatis suae, moveri incipiant; non posse centrum gravitatis ex ipsis compositae altius, quam ubi incipiente motu reperiebatur, ascendere.’

5) Voir, au Tome VIII, les pièces N^os. 2260, 2270 et 2365.

6) Voir les pièces N^os. 2267 et 2341.

7) Voir la pièce N^o. 2426.

[p. 404]

nement, en faisant voir la fausseté de son principe; sçauoir que la vitesse totale du pendule composé est egale à la somme des vitesses de ses parties muës separement; mais par ce que le mesme Mr. Bernoully en suiuant ses raisonnemens trouue encore que Mr. Huguens se trompe, j'ay creu qu'il ne seroit pas hors de propos, afin de leuer toute sorte de scrupule, d'apporter icy les raisons physiques et naturelles, qui seruent à demonstrer la verité tant de la Regle que de l'hypothese de Mr. Huguens.

Soit la ligne horizontale f B inflexible, et sans pesanteur, mobile autour du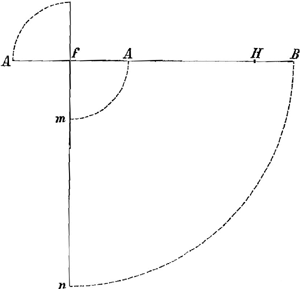



point fixe f, dans laquelle soient enfilés les deux poids egaux A et B, de sorte que Af soit vn pied et Bf quatre pieds; il faut trouuer la longueur f H du pendule simple jsochrone, jl est constant 1^o. que tous les corps pesants grands et petits commencent leurs descentes estant sur des plans egalement juclinés auec la mesme vitesse que j'appelle 1.⁸⁾ 2^o. que pour auoir la quantité de mouuement d'un corps, jl faut multiplier sa masse par sa vitesse, d'où jl est visible, que la quantité de mouuement auec laquelle le corps A commence à descendre separement estant au bout du pendule simple f A, sera egale à la quantité de mouuement, auec laquelle le corps B commence à descendre separement estant au bout du pendule simple fB, car les corps estant egaux, A 1 = B 1. Jl est visible de plus que si la vitesse, ou la

8) Voir, sur l'usage fait ici du mot ‘vitesse’, la remarque de Huygens dans sa lettre à de l'Hospital du 6 juillet, N^o. 2598, et la rédaction amendée de la pièce N^o. 2581, publiée dans l'Histoire des ouvrages des sçavans du mois de juin 1690, laquelle nous imprimons sous le N^o. 2605, comme Appendice I à la lettre d'envoi de Chr. Huygens à Basnage de Beauval, N^o. 2604.

[p. 405]

quantité de mouuement⁹⁾, auec laquelle le corps A tend à descendre separement, n'estoit que la quatriesme partie de celle du corps B, le corps A n'apporteroit alors aucun changement à la descente du corps B dans le pendule composé. Jl reste donc trois quarts de la quantité de mouuement du corps A qui font effort en A et qui par consequent se doiuent distribuer en B et A et en f; or pour faire cette distribution l'on doit enuisager la verge B f comme vn leuier. donc, si nous nommons x la portion de cette quantité de mouuement qui doit estre adjoutée à celle que nous suposions au corps A scauoir ¼ A, celle qui appartiendra au corps B sera 4x, et celle qui se perdra sur le point fixe f, ou qui paroistra se perdre, (car l'on peut penser qu'elle se communique aux corps invisibles) sera 12x. Donc x + 4x + 12x = ¾ A donc x = 3/68 A donc ¼ A + x = 5/17 A qui est la veritable quantité de mouuement du corps A dans le pendule composé, et la divisant par A, l'on aura 5/17 pour la vitesse auec laquelle jl commence à descendre, et si l'on fait comme 5/17 est à 1 vitesse auec laquelle nous avons suposé que tous les corps pesans commençoient leurs descentes^a) ainsi f A 1 pied est à fH 3 pieds ⅖. ce sera la longueur du pendule simple isochrone, car les espaces estant entr'eux comme les vitesses, le temps doit estre egal, ce qui est tout à fait conforme à la Regle que nous donne Mr. Huguens¹⁰⁾, jl nous est facile d'examiner maintenant les hauteurs ausquelles les poids A et B remonteroient par la ligne fn perpendiculaire à l'horizon estant tombés en m et n, si nous suposons auec luy que dans cet jnstant leur lien commun soit rompu, et qu'ils remontent par la ligne fn iusque ou jls pourront auec leurs vitesses acquises dans ce mesme jnstant. En voicy le calcul Soit z la vitesse que le corps A. a acquise estant tombé de la hauteur d'un pied, et ayant commencé sa descente avec la vitesse 5/17 donc si l'on fait 5/17. 1∷z. 17/5 z. 17/5 z sera la vitesse que le mesme corps A aura acquise estant tombé de la hauteur 17/5 de pied, ayant commencé sa descente auec la vitesse 1; car les vitesses acquises en tems egal sont entr'elles en mesme raison que les vitesses auec lesquelles les corps ont commencé de descendre. Jl s'agit maintenant de trouuer la hauteur d'ou le corps A doit estre tombé ayant commencé de descendre auec la vitesse 1 pour auoir acquis la vitesse z^b), ce qui est facile en cette sorte; soit cette hauteur y, l'on aura

9) Lisez: vitesse, et la quantité de mouvement. Voir la lettre de de l'Hospital du 19 juillet 1690.

a) Parce que le poids au bas du pendule isochrone doit avoir la vitesse 1, avec laquelle tous les corps commencent leur descente [Christiaan Huygens].

10) En effet: (4² + 1²):(4 + 1) = 17:5.

b) Car alors avec la vitesse z il pourra remonter à cette mesme hauteur [Christiaan Huygens].

[p. 406]

17/5 z.z∷√ 17/5. √ y, donc y = 5/17 de pied. Car lorsque les corps tombent librement, les vitesses acquises sont entr'elles comme les racines quarrées des hauteurs d'ou jls sont tombés. L'on prouera par un raisonnement tout semblable que le corps B estant libre remontera à la hauteur 80/17 de pied, leur somme 85/17 = 5; ce qui fait voir la verité tant de l'hypothese de Mr. Huguens, que de sa proposition 4^o.

Comme l'on pouroit trouuer quelque difficulté dans le 2.^e cas, qui est lorsque le point de suspension se trouue entre les deux poids, je vais l'expliquer en peu de mots. Suposons donc que le poids A soit attaché de l'autre costé du point f à vn pied de distance l'on voit d'abord qu'afin que le pendule composé se meuue, jl faut que le corps A perde la quantité de mouuement qu'il a vers le bas et que de plus jl en acquiert vne vers le hault qui soit le quart de celle qui reste à B. Jl est euident de plus que cela ne se peut faire que par l'effort du poids B, et à l'ayde du point fixe f, de sorte que l'on doit enuisager le pendule composé B f A comme un leuier, cecy suposé, soit B - x la quantité de mouuement restante au corps B lors qu'il commence à descendre; celle qu'il aura jmprimée au corps A vers le hault sera ¼ A - ¼ x, donc la force x que l'on doit retrancher de B est telle qu'elle jmprime au corps A vers le hault à l'ayde du point f la quantité de mouuement 5/4 A - ¼ x; or par la proprieté du leuier le point fixe f contribuë à cet effet vne force telle que 3 x, c'est-à-dire que la force x appliquée en B agit sur le corps A de la mesme maniere que si la force 4x estant apliquée jmmediatement en A, poussoit le corps A vers le hault, et cette force deuant produire vn effect qui luy soit egal, nous auons 4 x = 5/4 A - ¼ x, donc x = 5/17 A donc B - x = 12/17 B. donc 12/17 sera la vitesse auec laquelle le corps B commencera à descendre dans le pendule composé, et par des raisonnemens semblables à ceux du cas precedent, l'on trouuera que la longueur du pendule simple jsochrone sera 5 pieds ⅔. ce qui s'accorde encore parfaitement auec la Regle de Mr. Huguens¹¹⁾.

11) Voir la note 2 de cette pièce. En effet: (4² + 1²):(4 - 1) = 17:3 = 5⅔.