Oeuvres complètes. Tome IX. Correspondance 1685-1690

[p. 439]

N^o 2598.
Christiaan Huygens au Marquis de l'Hospital.
6 juillet 1690.

La minute se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek¹⁾.
La lettre est la réponse au No. 2594.
De l'Hospital y répondit par le No. 2600.

Sommaire:	Pourquoy veut il que mon hypothese ne soit pas assez simple ni assez evidente pour être supposée sans preuve. Je n'en scay pas de plus certaine en mécanique, puis que j'ay fait voir que c'est la mesme chose que de dire qu'un corps pesant ne scauroit monter par la force de sa pesanteur. Mr. Paschal Torricelli et autres s'en sont servis.
	Pourquoy dit il que mr. Bernouilly a pleinement satisfait aux objections de l'Abbè Catelan? Je pretens que c'est moy qui y ai satisfait et que mr. Bernoully n'y a point satisfait ni qu'il n'a point démontrè la faussetè du principe de mr. l'Abbè comme je feray voir cy dessous. On doit trouver étrange cette entreprise de mr. Bernouilly, qui voit luy mesme et avoue qu'il doute de la veritè de son raisonnement.
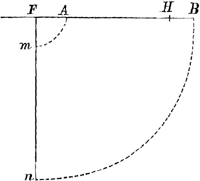
	Vous dites que mr. Bernouilly en suivant ses raisonnements trouve que je me trompe. Mais vous deviez avoir remarquè qu'il ne donne pas ses raisonnements pour certaines et legitimes. Et comment pouvez vous les admettre pour tels, puis qu'ils menent à des conclusions contraires aux vostres. Car il trouve que le centre de gr. des poids égaux A et B d'un pendule composè pareil au vostre (c'est à dire ou A est attachè à un pied de distance du point de suspension F et B à 4 pieds) monterait moins haut en les laissant monter séparement qu'il n'estait lors que le pendule commencoit à descendre. Et vous trouvez que ce centre de gr. remonte justement à sa premiere hauteur de mesme que moy. Si son raisonnement est bon, le vostre ne le sera donc point^2).

A Monsieur le Marquis de l'Hospital, chez Mr. le Comte de S.^te Mesme. Rue des bons enfans proche de la place des victoire a Paris.

A la Haye, ce 6 Juillet 1690.

Vostre lettre, Monsieur, du 2 Juin m'a esté rendue. Et suivant ce que j'ay promis, je vous envoie mes remarques sur vostre solution³⁾ du probleme du pendule

1) Chr. Hugenii Exercitationes Mathematicae etc. Fasc. I, page 223.

2) Ce sommaire ou avant-projet se trouve à la page 50 recto du livre G des Adversaria. Au revers de cette page on rencontre encore un petit calcul avec l'en-tête: ‘Examiner en général la manière du marquis de l'Hospital’. Huygens y vérifie, pour le cas général BF = a, AF = b, l'identité du résultat, obtenu en appliquant la manière de de l'Hospital, avec le sien propre. Il conclut comme il suit: ‘Sa manière respond donc tousjours à la mienne, quoyque je ne vois pas comment il peut y estre arrivè, puis qu'il se sert de raisonnements faux. Il aurait bien de la peine en mettant trois poids égaux au pendule.’
De plus, on trouve sur les pages qui précèdent des phrases plus au moins détachées qui se rapportent à la Lettre N^o. 2580, à l'Appendice N^o. 2581 ou à l'article de Bernoulli (notre pièce N^o. 2426). Puisque les remarques qu'elles contiennent se retrouvent pour la plupart sous une forme peu modifiée dans les autres pièces que nous reproduisons, nous nous bornerons à en citer la phrase suivante qui nous semble assez remarquable et qui diffère aussi un peu plus que les autres de la leçon correspondante que l'on rencontre dans la lettre qui va suivre:
‘J'avais considerè comme eux (c'est-à-dire Bernoulli et de l'Hospital) que le poids le plus proche de la suspension faisait effort pour hater le mouvement du poids d'en bas; mais estant difficile de dire de combien il le devoit faire hater, j'ay cherchè cela par une voie assurée et ou je suivais des principes tres certains. Il paroit qu'il estoit difficile de l'autre manière quand on considere comment vos raisonnements se contrarient.’

3) Voir la pièce N^o. 2581.

[p. 440]

isochrone. des quelles vous jugerez, et si vous trouvez que vostre raisonnement puisse subsister, en satisfaisant à mes difficultez, rien n'empeschera que nous ne fassions paroitre l'un et l'autre dans nos Journaux. J'ay mesme quelque raison de souhaiter que cela se fasse, pour publier à cette occasion mon sentiment touchant l'examen de Mr. Bernoulli⁴⁾, qui est raporté au mois de Juill. en 1686. Mais il nous importe à tous deux que ce que vous avez dessein d'avancer en ma faveur, ne contiene rien que de veritable.

C'est pourquoy voions ce qu'on y peut objecter.

Dans vostre Extrait de lettre, devant que de venir au probleme du centre d'oscillation, il y a deux choses que je ne puis passer sans en rien dire. La premiere est que mon hypothese, qui sert de fond a ma prop. 4 ne paroit pas assez simple, ni assez évidente pour estre passée sans preuve. Pour moy je ne connois pas de principe plus certain en mechanique que cette hypothese, puis que j'ay fait voir que c'est la mesme chose que de dire, qu'un corps pesant ne scauroit monter par la force de sa pesanteur. Mrs. Paschal⁵⁾, Torricelli⁶⁾, et autres s'en sont servis et Mr.

4) Voir la pièce N^o. 2426.

5) Au Chapitre II du ‘Traité de l'Equilibre des Liqueurs’ cité dans la Lettre N^o. 1922, note 3.

6) Dans le Traité:
‘De motu gravium Naturaliter descendentium, Et Projectorum Libri Duo. In quibus ingenium naturae circa parabolicam lineam Ludentis per motum ostenditur, Et universa Projectorum doctrina unius descriptione semicirculi, absolvitur’.
Torricelli fait précéder la Propositio I, par le principe suivant: ‘Duo gravia simul coniuncta ex se moveri non posse, nisi centrum commune gravitatis ipsorum descendat’.
Pascal et Torricelli n'ont appliqué le principe dont parle Huygens qu'à des questions de statique.

[p. 441]

Bernoulli l'appelle le grand principe de mechaniques et avoue qu'il n'en peut revoquer la verité en doute. Vous dites en second lieu que Mr. Bernoully a pleinement satisfait aux objections, que Mr. l'Abbè Catelan avoit formées contre ma Theorie, en faisant voir qu'il s'appuioit sur un faux principe. Il semble à la veritè que Mr. Bernouilly avoit entrepris de refuter le principe de Mr. l'Abbè, mais il doit avouer, qu'il ne l'a pas fait, puis qu'il donne à connoitre luy-mesme qu'il ne scait pas bien comment il faut poursuivre sa demonstration en disant, Rogantur hac occasione eruditi etc. Et en attendant leur avis ou secours, il suppose mais douteusement la solution de ce qu'il leur demande par ces mots: si namque celeritatis excessus ita distribueretur, ut etc. Alors il trouve que le principe de Mr. Catelan



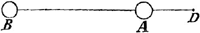
seroit faux. Car dans le pendule DAB, dont les poids A, B, sont egaux et la distance BD au point fixe quadruple de AD, les vitesses acquises de A et B, quand ils descendent conjointement, c'est à dire, en faisant un pendule composè, seroient 9/17 et 36/17, dont la somme est moindre que celles de leur vitesses acquises, quand ils descendent separement, scavoir que 1 + 2. Car l'une somme est 2 11/17 et l'autre 3. Mais ces sommes selon le principe de Mr. Catelan devoient estre egales. donc Mr. Bernouilly auroit refutè ce principe en cas que sa supposée distribution fust veritable, mais c'est ce qu'il n'assure pas.

Et vous, Monsieur, vous ne scauriez douter que cette supposition de Mr. de Bernouilly ne soit fausse, puis qu'elle mene à une conclusion contraire à la miene et à la vostre, qui sont les mesmes. Car il trouve que les quarrez des dites vitesses 9/17 et 36/17, qui sont 81/289 et 1296/289 font ensemble 4 13/17, qui, selon nous, devoient faire 5. Je ne comprens donc pas comment vous pretendez que Mr. Bernouilly ait pleinement satisfait aux objections de Mr. l'Abbé Catelan. Et il me semble que vous pouriez dire cela à meilleur droit de la derniere response que je luy ay faite⁷⁾. Je ne comprens pas non plus le dessein de Mr. Bernouilly, qui entreprend de refuter Mr. l'Abbè par un raisonnement, qu'il avoue luy mesme estre douteux, et au lieu de soutenir ma proposition, qu'il dit estre fondée sur le grand principe des mechaniques, tourne ce mesme raisonnement incertain contre moy, comme s'il estoit capable de mettre en doute la verité de ma Proposition.

Je viens, Monsieur, à vostre demonstration, ou plustost nouvelle recherche du

7) Voir la pièce N^o. 2341.

[p. 442]

Pendule isochrone à celuy qui est composè de deux poids tels que cy-dessus. Je vois que par vostre methode vous trouuez la mesme chose que moy, et je ne vois pas pourtant comment vous y estes parvenu par vostre maniere de raisonner, qui me semble non seulement peu evidente, mais aussi en partie peu veritable.

Vous dites qu'il est constant que tous les corps pesants, grands et petits, commencent leurs descentes, estant sur des plans egalement inclinez, avec la mesme vitesse. Il faut voir comment vous concevez cette vitesse au commencement de ces descentes. Selon moy, on ne peut pas dire que les corps pesants ayent une certaine vitesse dans ce commencement, puis qu'ils passent par des degrez de vitesse infiniment petits, quoy que je me souviene que Mr. Mariotte et le Pere des Chales ont voulu soutenir le contraire.

On peut pourtant comparer les vitesses des corps au commencement de leur descente par les espaces qu'ils parcourent dans un mesme temps quelque petit qu'on le prenne. Et c'est ainsi que j'explique vos comparaisons de ces vitesses commencantes. Comme quand vous mettez 1 pour la vitesse au commencement de la descente perpendiculaire de tout corps pesant, et que vous trouvez cette vitesse 5/17 dans un corps qui fait partie d'un pendule.

Je puis comprendre de mesme la quantitè de mouvement d'un corps au commencement de sa descente que vous faites naitre en multipliant sa masse avec cette premiere vitesse.

Vous dites en suite: Il est visible de plus que, si la vitesse ou la quantité de mouvement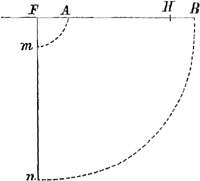



avec la quelle le corps A tend à descendre separement, n'estoit que la quatrieme partie de celle du corps B, le corps A n'apporteroit alors aucun changement à la descente du corps B dans le pendule composè.

Si le corps A estoit donc ¼ de B, et ainsi selon vous sa quantité de mouvement pour descendre separement ¼ de la quantité du mouvement pour descendre du corps B, vous diriez que ce corps A n'apporteroit alors aucun changement à la descente du corps B, dans le pendule composè, ce qui pourtant est visiblement faux. Comment se peut on donc fier à vostre raisonnement qui mene à cette absurdité? Mais supposons que vous ayez pu separer, comme vous faites, ce quart du mouvement du corps A, il reste donc, dites vous, ¾ de la quantitè du mouvement du

[p. 443]

corps A, qui font effort en A, et qui, par consequent, se doivent distribuer en B en A et en F, &c.

Icy je ne comprens nullement la raison de la distribution que vous faites. Car si vous considerez le pendule FAB comme un levier qui tourne sur le point F, les ¾ restants du mouvement du corps A, qui font effort en A, font seulement un quart autant d'effort sur le corps B. Cependant vous attribuez une partie quatre fois plus grande de ces ¾ au corps B qu'au corps A. Vous voulez dire, comme je crois, que la vitesse, qui en revient au corps A, doit estre la quatrieme partie de la vitesse qui en revient au corps B, parce qu'ils sont attachez à la mesme verge FB. Mais lors qu'en suite vous donnez des mesmes ¾ trois fois plus au point fixe F, qu'au corps B, vous revenez, je ne scay comment, à la pression que font les ¾ sur A: et considerant FB comme un levier appuiè par les deux bouts F et B, vous donnez trois fois autant de cette pression au point fixe F qu'au corps B. Et de ce que vous avez trouvè par ces deux manieres de levier, vous concluez qu'au point F il appartient 12 parties des dits ¾ de mouvement, au corps A une, et au corps B 4.

Tout cecy n'est pas bien intelligible, pour ne rien dire de cette perte du mouvement, attribuée au point F, que vous concevez se communiquer aux corps invisibles, des quels je ne scaurois approuver icy la consideration. La chose qu'on cherche, estoit de scavoir de combien le corps A doit haster le mouvement de B dans le pendule composé, car on voit assez facilement qu'il le doit haster, mais de dire à quel degrè, c'est ce qui est fort difficile. Et je n'ay point trouvè de raisonnement seur et evident pour parvenir à cette determination, qu'en me fondant sur ce que les poids, en quitant le pendule lors qu'il est descendu, et montant separement ne devoient pas porter leur centre commun de pesanteur ni plus haut ni plus bas que d'où il estoit venu, mais justement à la mesme hauteur. Et cela je le prouve par le grand principe des mechaniques, outre que ma theorie convient exactement avec l'experience. Vous deviez un peu essaier la vostre dans un pendule composè de plus que de deux poids, et je crois qu'alors vous auriez bien de la peine à donner la longueur du pendule isochrone, et encore plus, si les poids n'estoient plus enfilez à une mesme ligne droite. Mais je puis me tromper; et vous trouverez peut-estre moyen de rendre vostre methode generale, et en mesme temps plus claire, estant vraisemblable qu'elle n'est pas sans fondement, puis qu'elle produit la mesme chose que la miene. An reste, Monsieur, si vous approuvez ce que j'ay remarquè à l'egard de Mr. de Bernouilly^a), et si vous croiez encore pouvoir montrer que son principe bien entendu confirme ma Theorie, vous me ferez plaisir de me conseiller de quelle maniere nous pourrions faire entrer nos remarques dans le Journal, car vous avez raison de dire qu'il ne faut pas le laisser sans replique. Je suis parfaitement etc.

Je n'ay pas encore eu de nouvelles, si les exemplaires de mon Traitè de la Lu-

a) Journ. de Leipsich chez Geselle⁹⁾ [Christaan Huygens].

9) Le libraire cité dans la Lettre No. 2569, note 1.

[p. 444]

miere ont estè recus par Mr. de la Hire⁸⁾, ce qui me met en peine et m'empesche d'en hazarder d'autres.

8) Voir les Lettres N^os. 2579 et 2589.

9) Le libraire cité dans la Lettre No. 2569, note 1.