Oeuvres complètes. Tome IX. Correspondance 1685-1690

[p. 80]

N^o 2426.
Jac. Bernoulli.
juillet 1686.

La pièce a été publiée dans les Acta Eruditorum¹⁾.

Dn. Bernoullii Narratio controversiae inter Dn. Hugenium & Abbatem Catalanum agitatae de Centro Oscillationis, quae loco Animadversionis esse poterit in Responsionem Dn. Catalani, num. 27. Ephem. Gallic. Anni 1684. insertam²⁾.

Excerpta ex Litteris Dn. Bernoullii Lipsiam missis.

Mense Septembri anni 1681 Abbas Catelanus propositionem quandam tractatus Cl. Hugenii, quem de Horologio Oscillatorio inscripserat, adortus est³⁾, formata contra illam objectione; in qua quia mentem suam minus feliciter expressit, ansam dedit isti controversiae, quae hucusq; fere inter illos viguit. Verum quidem est, eum initio. a. 1682⁴⁾. objectioni suae additis paucis lineis variationem quandam induxisse; sed quoniam ejus partes satis adhuc male cohaerentes reliquit, eam in mente Lectoris sui excitavit opinionem quasi persuasum haberet, summas altitudinum, e quibus pondera alicujus penduli junctim descendunt, & ad quas postmodum separatim ascendunt, inaequales esse debere hanc solam ob causam, quod priores altitudines sint proportionales ipsis ponderum celeritatibus, posteriores vero non nisi quadratis istarum celeritatum. Quare etiam Hugenius, id unicum Catelano scrupulum movere ratus, respondere abstinuit, usqe in mensem Junium, quo tandem calamum arripuit⁵⁾, ac exemplo duorum numerorum 5 & 10, duorumque aliorum 3 & 12 breviter monstravit, fieri utique posse, ut binae quantitates eandem cum binis aliis conficiant summam, etiamsi diversam ab illis rationem habeant, neque tum temporis in dubium revocavit πρῶτον Catelani ψεῦδος, quod tamen in prima jam objectionis suae impressione manifeste satis prodiderat, dum supposuit: Pendulum ex duobus ponderibus compositum, eandem acquirere celeritatem, quantam acquir at summa pendulorum simplicium; id vero sicco pede praeteriit Hugenius, vel quod non penetrarit statim, ob nullam periodorum connexionem, quorsum falsa ista Catelani suppositio tenderet, vel potius quod illi ceu verisimili admodum

1) De Juillet 1686, pages 356 et suiv.

2) Voir la pièce N^o. 2365.

3) Voir la pièce N^o. 2260.

4) Voir la pièce N^o. 2260, note 1.

5) Voir la pièce N^o. 2267.

[p. 81]

tum ipsemet adstipularetur. Catelanus interea Hugeniano responso non contentus, excepit 20 Julii 1682⁶⁾, ac terminis Algebraicis rem aggressus est, eodem innixus fundamento: Quod totalis celeritas penduli compositi aequet summam celeritatum partium ejus separatarum. Quo facto controversiaista ultra annum sopita jacuit. Me quod spectabat, cui Hugenii liber tum nondum visus, nedum lectus fuerat, scopum alium non habebam⁷⁾, quam illustrare ejus responsionem, remque examinare, qualiter ab ipso examinata, atque in Actis recensita fuerat. Animadvertens itaque, Catelani principium ab Hugenio non refutatum esse, & ego illud intactum reliqui, sufficere mihi ratus, si Hugenianum responsum simpliciter applicarem ad praesentem controversiam, proposito eum in finem exemplo penduli, e duobus aequalibus ponderibus compositi; ubi innuere saltem volui, quod supposito pro totali ejus celeritate numero ternario (quicquid statuatur de celeritatibus utriusque separatim spectati ponderis, dummodo eae sint in ratione 2 ad 1) quadrata 144/25 & 9/25 ex mente Hugenii significare debeant non nisi rationem altitudinum, ad quas ascendant separata pondera, minime vero ipsas altitudines (quod ipse quoque postmodum indigitavit Hugenius in secunda responsione⁸⁾, 8 Jun. 1684) partim quoniam celeritates atque altitudines, utpote quantitates heterogeneae, se mutuo mensurare non possunt; partim etiam, quia ipse Catelanus urgere saltem videbatur, altitudines esse proportionales quadratis, vel sicut quadrata celeritatum; tametsi in proxime sequenti calculo quadrata ista pro ipsis altitudinibus adhibuerit. Comparato mihi paulo post, & perlecto Hugenii libro, animadvertebam, Propositionem controversam ex priore Hypothesium, quas Auctor initio stabiliverat, adeo evidenter inferri, ut neutra infringi possit, quin simul evertatur altera; quocirca judicabam, si Catelano falsa fuisset visa propositio, eum potius ipsam adoriri debuisse Hypothesin, magnumque illud inibi contentum Principium Mechanicum. Verum enim vero cum hujus principii veritatem nullo jure in dubium revocare possem, atque simul etiam seriem ratiocinii a Catelano satis confuse propositi evolvere coepissem, errorem ejus detexi illico, falsamque cognovi esse, qua nitebatur, regulam, nimirum: Celeritatem totalem penduli compositi aequalem esse summae celeritatum partium ejus separatarum. Atque ut ostendam, animadversum mihi fuisse errorem, priusquam Hugenii epistola de 8. Jun. lucem aspexisset, afferam hic causam physicam, omissam ab Hugenio, qua fit, ut penduli compositi celeritas perpetuo minor sit celeritate partium ejus separatarum: Ponamus majoris evidentiae ergo, pondera penduli A & B in linea inflexili DB⁹⁾ libere hinc inde moveri posse, sic ut linea haec, dum rotatur circa axem D, quamvis secum rapiat pondera, non tamen impediat descensum illorum in linea recta versus centrum Terrae. Quo posito,

6) Voir la pièce N^o. 2270.

7) Voir la pièce N^o. 2332.

8) Voir la pièce N^o. 2341.

9) Voir la figure de la page suivante.

[p. 82]

constat, utrumlibet pondus sigillatim dimissum, eadem celeritate latum iri, qua ferretur absque virga DB, utpote nec a virga, nec ab ejus axe ullo modo impeditum;



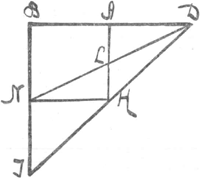id est si pondus A absque virga certo tempore conficit spatium AH, & pondus B spatium aequale BN, utrumque etiam cum virga, sed sigillatim, dimissum eodem tempore idem spatium AH & BN conficiet. Constat insuper, quod si gravitas in utrumque pondus ageret viribus, quae proportionatae forent ipsorum respectivis ab axe distantiis, virga nullum adhuc ipsorum descensui afferret impedimentum, propterea quoniam exacta certo tempore unum eorum reperiretur in H & alterum in I, vel prius in L, posterius in N, sive absque virga, sive cum virga, sive sigillatim sive conjunctim dimitterentur. Verum enim vero quoniam gravitas in utrumque pondus agit viribus aequalibus, sic ut pondera eodem tempore aequalia spatia AH & BN transigere annitantur, & tamen interea pondus A junctim dimissum, ob inflexilem virgam, nequit pertingere nisi ad L, dum pondus B jam est in N, hinc sequitur, gravitatis vim in pondere A non esse exhaustam; adeoque residuum harum virium, ex una parte urgere debere corpus B, ex altera ipsum axem D, eundemque premendo aliquam sui partem ibidem insumere & deperdere; siquidem virga hocce casu instar vectis considerari possit; prout extra dubium est, quod si corpus B infinite tarde moveri, id est, firmum & stabile esse intelligatur, sicut axis D corpus A partem sui ponderis, aeque in axem D atque in corpus B transferret. Ex hactenus dictis colligere proclive est, si quis examinare vellet, quantam partem celeritatis suae pondus A in premendo axe D consumere debeat, eum exinde, imitando Dn. Catelani ratiocinium, veritatem aut falsitatem Hugenianae Hypotheseos, inque hac fundatae Propositionis detegere posse. Rogantur hac occasione eruditi, ut examinent, qualem legem communicationis celeritatum observent corpora mota, quae ex una parte innituntur sirmo fulcimento, ex altera alii corpori itidem, sed tardius moto: si namque celeritatis excessus, qui hinc inde communicandus est, in eadem ratione distribueretur, in qua distribuitur onus aliquod, quod vecti duobus sustento fulcris impositum est, nimirum in ratione reciproca distantiarum mobilis a fulcris¹⁰⁾, tum imitando ratiocinium Dn. Catelani, deprehenderemus, summam altitudinum, ad quas ascendunt separata penduli pondera, vicissim nunc minorem

10) On verra dans la correspondance de 1690 comment De l'Hospital a su fonder sur le principe énoncé ici, en l'appliquant d'une manière plus heureuse, une détermination exacte du centre d'oscillation d'un nombre de poids distribués sur une même droite, passant par le point d'appui. Consultez, entre autres, son article dans ‘l'Histoire des ouvrages des Sçavans’ de juin 1690.

[p. 83]

esse summa altitudinum, e quibus antea conjunctim descenderant, quod iterum Hugenianam Propositionem everteret.

En calculum: Esto altitudo AL = 1 ped.

Altitudo BN = 4 ped.

Celeritas ponderis A acquisita in puncto L, ubi descendit separatim = 1.

Celeritas ponderis B aequisita in puncto N, quando cadit separatim = 2.

Celeritas ponderis A acquisita in puncto L, quando descendit conjunctim = x.

Igitur Excessus celeritatis ponderis A, qui tam in axem, quam in pondus B redundat	= 1 - x.
Et pars hujus excessus, quae soli ponderi B communicatur	= ¼ - ¼x.
Tota ergo celeritas ponderis B in puncto N cum conjunctim cadit	= 2¼ - ¼x.

Atqui vero 2¼ - ¼x, x∷4, 1. Igitur x = 9/17 & 4x = 36/17 eorumque quadrata 81/289 & 1296/289 quorum summa 4 13/17 minor est 1 + 4 = 5. Antequam finiam, in favorem Dn. Catelani hoc monebo, quod etiamsi commune gravitatis centrum juxta illum altius ascendere deberet, quam descendit, nondum tamen sequatur, repertum fore motum perpetuum, ut sibi persuadet Ill. Hugenius; quoniam in istis abstrahi solet ab aeris resistentia, a diminutione celeritatis, quae necessario sequitur disruptionem vinculi, quo connectebantur partes penduli, aliorumque obstaculorum; prout ipsa quoque haec aeris resistentia in causa est, cur simplex pendulum motum suum non continuet, ut maxime in Hypothesi Hugeniana ad eandem ascendere debeat altitudinem, a qua descendit¹¹⁾.

11) Nous renvoyons, pour la réponse de Huygens aux objections contenues dans cette lettre, à la correspondance de 1690, notamment à l'article de Huygens dans le numéro de juin 1690 du recueil suivant:
Histoire des ouvrages des Sçavans, Par Monsr. B*** Docteur endroit. A Rotterdam, chez Reinier Leers m.dc.lxxxviii. Avec privilege de Nos Seigneurs les Etats de Hollande et de West-Frise. in-12^o.
Une réimpression, publiée à Amsterdam en 1721, chez Michel Charles le Cene, mentionne comme auteur: Mr. Basnage de Beauval. Dans la préface, celui-ci dit qu'en avril 1687, lors de la maladie de P. Bayle, il avait entrepris la rédaction des Nouvelles de la République des Lettres, mais que ses engagemens particuliers pour Rotterdam, l'abondance des meilleurs livres qui se trouvent chez Leers, l'avaient décidé à changer d'éditeur et à donner un titre nouveau à la publication. Les Nouvelles de la République ont continué de paraître chez Desbordes, mais sous une autre rédaction que celle de Bayle.
Henri Basnage de Beauval naquit à Rouen, le 7 août 1656, et fut avocat au parlement. La révocation de l'édit de Nantes le contraignit, en 1687, à se réfugier en Hollande. Il y mourut le 23 mars 1710.