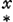Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–
[pagina 74]
| |||||||||||||||||||
No 2672.
| |||||||||||||||||||
[pagina 75]
| |||||||||||||||||||
point D, auquel OF continuée rencontre le quart de circonference GDC, et que mesme par cette quadrature donnée vous trouvastes l'equation de la courbe. Or a cause qu'il pourroit arriver que j'eusse a prouver ce fait a Mons.r Leibnitz, je vous supplie Monsieur de me permettre, et de me donner moien en faisant response a ce billet, de pouvoir alleguer vostre temoignage pour confirmation de ce que je viens de dire, estant seulement besoin de designer la courbe par son equation que vous trouvastes xxyy∞aayy-aaxx. Vous ferez plaisir et obligerez beaucoup
Vostre tres h. et tres ob. serviteur Hugens de Zulichem.
Pour Monsieur Fatio de Duillier. Ga naar voetnoot7) y 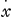 =Fluxion de l'Espace AOF
a =Fluxion de l'Espace AOF
a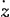 =Fluxion du rectangle BLGa naar voetnoot8). Donc y =Fluxion du rectangle BLGa naar voetnoot8). Donc y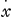 =a =a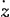
a2-2az+z2=a2-x2; dont la Fluxion donne -a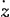 +z +z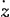 =-x =-x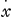 . Et prenant les valeurs de . Et prenant les valeurs de 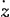 on aura
y on aura
y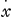 /a=-x /a=-x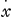 /-a+z. Et ay-zy=ax. Or z=a-√ax-x2. /-a+z. Et ay-zy=ax. Or z=a-√ax-x2.
Ainsi ay-ax=ay-y√a2-x2Ga naar voetnoot9). Et a2x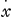 =a2y =a2y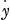 -y2x -y2x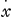 -x2y -x2y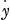 sera sa Fluxion. sera sa Fluxion.
| |||||||||||||||||||
[pagina 76]
| |||||||||||||||||||
Dans cette equation on peut substituer les valeurs des Racines ax, ou ay, ou xy.
Dans le 1er Exemple il est aisé de reconnaitre les Generateurs a2y2-x2y2. Et comme c'est là la quantité meme qui est sous le Signe Radical, il est à presumer que cette Racine tient lieu de ax qui paracheveroit le quarré a2x2. Et effectivt on trouvera que ces trois Generateurs rendent l'Equation marquée I. La même chose se doit entendre de l'Equation II. De même dans la III Equation, il faut voir si sa Generatrice n'est pas x2y2==a2y2-a2x2. Et dans la IV Equation ci dessous il faut voir si-yx+√a2y2+2a2xy=ax? De cette maniere on parviendra à la veritable Generatrice, si elle a produit la Fluxion proprosée par ces sortes d'Enveloppemens. Et ceci donne une clef considerable pour trouver les Fluentes ou Generatrices, quand leurs Equations sont simples en elles mêmes, quoi que leurs Fluxions soient mêlées de Racines par accident.
Ga naar voetnoot10) Mr. Hugens de la Haye 3 avril 1691, le lendemain de l'Ensevelissement de Mr. Ellys Esq.e à N.F. à la Haye. Il me redemande la lettre où je lui avois expliqué autrefois ma Methode inverse des Tangentes et souhaite ce que je puis encore avoir ajouté à cette methode. | |||||||||||||||||||
[pagina 77]
| |||||||||||||||||||
Ou qu'au moins je lui explique les deux Exemples que j'ai donnés dans les courbes qu'il avoit proposées à Mr. Leibnitz et a moi. Il rend temoignage aux progrès que Mr. Leibnitz et moi avons fait en cette matiere, desquels il aime mieux profiter que travailler sur les fondemens contenus dans ma Lettre, et peut estre sans succès. Sur l'Echange que Mr. Leibnitz proposoit de son secret, pour avoir une solution du probleme susdit de Mr. Hugens, s'il y avoit des racines composées dans l'Equation de la Tangente. Probleme que Mr. Hugens m'avait proposé il y a longtemps et dont je luy avois donné la Solution pour retrouver l'Equation de certaine Courbe par la propriété de sa Quadrature. Cette courbe avait pour Equat.n x2y2=a2y2-a2x2. Mais la propriété de sa Tangente contient une Racine incommensurable complexe, si on y substitue la valeur de xy ou de ay, ou de ax, etc. Mr. Hugens demande que je lui laisse alleguer à Mr. Leibnitz mon Temoignage sur ce fait. J'ai ajouté ici ma solution ou mon Analyse de ce Probleme de Mr. Hugens. NB. Remarque considerable sur les Racines complexes. |
|