Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–
[pagina 192]
| |||||||||||||||||||||||||||||||||||||||||||
No 2710.
|
| Ergo secunda summa=2s-d secantium ad ½ gr. | } vera major. |
| et tertia+4s-3d secantium ad ¼ gr. | } vera major. |
| et quarta=8s-7d secantium ad ⅛ gr. | } vera major. |
| et quinta=16s-15d secantium ad 1/16 gr. | } vera major. |
Sed quia semper tantum unam d amplius auferendo, oritur s-d multiplex per numerum competentem progressionis 1, 2, 4, 8, 16, etc.+d. d autem infinite parvum fit respectu multiplicis s: hinc patet multiplicem s-d, seu ms-md, tandem accipi posse pro ms-md+d. m numerus seriei 1, 2, 4, 8, 16 etc.
Itaque si velim comparare primum summam secantium ad gradus integros, cum summa totidem radiorum, erit earum ratio ut s ad nr ponendo n=numero graduum in arcu proposito; at si velim comparare summam secantium ad infinite parvas particulas graduum, cum summa totidem radiorum, earum ratio erit proxime quam ms-md ad nmr, hoc est quam s-d ad nr; cum alioqui ratio ista esset ut s ad nr.
Itaque cum ad arcum 45 gr. summa secantium ad gradus singulos seu s, sit inventa 507081503 ad datum radium 10000000 et totidem radii faciant 450000000=nr. d autem seu ½ DC tunc sit 2071068: Si ab s auferatur haec d, fiet 505010435 quae ad 450000000 proxime majorem rationem habebunt quam summa secantium crescentium cum minimis particulis graduum, usque ad 45 gradus ad summam totidem radiorum.
Sed adhuc propius accedemus si sit s summa secantium ad singulos dimidios gradus quam invenimus additione ex tab. sinuum esse 1012061091; tunc enim n=90 et nr=900000000 et s-d=1009990023. Eritque ratio summae secantium ad minimas particulas graduum ad summam totidem radiorum proxime major ut 1009990023 ad 900000000, hoc est ut 504995012 ad 450000000Ga naar voetnoot2).
§ II.
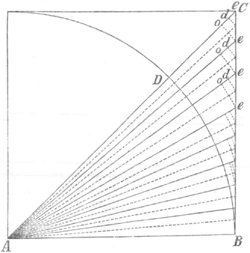
Inventio termini minoris summae infin. secantium ad totidem radios.
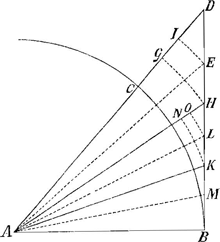
Ut GD ad DI differentiam inter DA, EA ita sit CD ad aliam P. Hâc ablatâ a summa secantium DA, HA, KA, reliquum minus erit summa secantium EA, LA, MA.
Adeoque si a dupla summa secantium DA, HA, KA auferatur P, reliquum minus erit summâ tangentiumGa naar voetnoot3) DA, EA, HA, LA, KA, MA. Unde (per progressionem sicut pag. 26 lib. G)Ga naar voetnoot4) erit ratio summae secantium DA, HA, KA, minus P, ad totidem radios, semper minor ratione infinitarum secantium ad totidem radios.
Ratio est quod auferendo DI ab DA, fit qui-
dem EA, sed in caeteris nimium aufertur, cum ab HN ex. gratia aufertur pars proportionalis ejus in eadem ratione GD ad DI. Hoc autem fit in caeteris omnibus secantium primarum differentiis, quandoquidem totius CD pars proportionalis ejusmodi aufertur.
| sec. 45o | 14142136 | 14142136 |
| sec. 44o 30′ | 14020321 sec. 44o 45′ | 14080831 |
| _____ | _____ | |
| 121815 GD: | 61305 DI=4142136 DC: 2084584 | |
| 1012061091 | ||
| 2084584 | ||
| _____ | ||
| 1009976507 | ||
| 3 | ||
| _____Ga naar voetnoot5) | ||
| 3029929521 minor vero | 30299392 verus | |
| 30299392 verusGa naar voetnoot6) | 30299700 majorGa naar voetnoot7) | |
| _____ | _____ | |
| 97 diff.a | 308 diff.a |
minor terminus propior quam terminus major.
- voetnoot1)
- Cet Appendice contient les règles pour le calcul d'une limite supérieure et d'une limite inférieure de l'intégrale
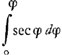 et leurs démonstrations. Le § I, qui se rapporte à la limite supérieure, est emprunté à la page 64 recto du livre G; d'après le lieu qu'il y occupe, il doit être daté probablement d'octobre ou de novembre 1690; le § II est tiré du manuscrit cité dans la note 15 de la Lettre No. 2709. Ce § II est d'une date postérieure, plus difficile à préciser.
et leurs démonstrations. Le § I, qui se rapporte à la limite supérieure, est emprunté à la page 64 recto du livre G; d'après le lieu qu'il y occupe, il doit être daté probablement d'octobre ou de novembre 1690; le § II est tiré du manuscrit cité dans la note 15 de la Lettre No. 2709. Ce § II est d'une date postérieure, plus difficile à préciser.
- voetnoot2)
- Plus tard Huygens ajouta à cette pièce: ‘Hic usus in dimetiendo spatio ALREB pag. 17 in fine (voir le § I de la pièce No. 2634) quod idem metiri licet, ut postea feci, pag. 90 et 91 (voir la note 26 de la pièce No. 2625) per inscripta rectangula et circumscripta; sed haec methodus melior’.
- voetnoot3)
- Lisez: secantium.
- voetnoot4)
- Voir le § I de cette pièce.
- voetnoot5)
- La multiplication par 3, ou plutôt par 30, a pour but de réduire la somme trouvée des sécantes, qui correspond à une somme de 90 rayons, au cas mentionné dans le texte de la Lettre No. 2709, où l'accroissement par minutes exige une somme de 2700 rayons.
- voetnoot6)
- Ce nombre a été trouvé au moyen des logarithmes. Comparez le texte de la Lettre No. 2709.
- voetnoot7)
- Nombre obtenu en multipliant par 3 le nombre 1009990023 trouvé vers la fin du § I.