Oeuvres complètes. Tome I. Correspondance 1638-1656

[p. 304]

N^o 204.
Christiaan Huygens à Fr. van Schooten.
Appendice au No. 203.

La minute et la copie se trouvent à Leiden, coll. Huygens.

pag. 33.^1) Quae quidem inventu difficilior non fuisset quam IL, ad hunc locum annotavi sic^2).

Si termini OX et p/m xx defuerint, manifestum est fieri LC ∞ m. Quare ad hunc casum construendum ab initio debuit sumi BK ∞ 2m, ducique KI, et IL ut prius. eritque punctum quaesitum in linea recta IL.

Si vero defuerint termini mm et OX, ideoque LC ∞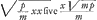 nam haec eandem quantitatem significant;



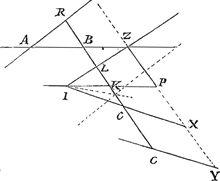
ad hujus constructionis casus oportet à puncto Z intersectione nimirum rectarum AB, IL, ducere ZX parallelam BK, quaeque ad ZA eam habeat rationem quam √mp ad m: deinde vero ducta IX in ea ubique reperietur punctum C quaesitum. Quod evidens fiet si producatur IK ad P. nam quia IK ∞ AB et KP ∞ BZ erit tota IP ∞ AZ. fecimus autem AZ ad ZX ut m ad √mp. Ergo et IP ad ZX hoc est IK ad LC ut m ad √mp. Est autem IK ∞ x. Ergo fit LC ∞ 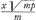ut oportebat. Denique si OO aequalis sit 4 pm, et eodem signo affectae quantitates mm et pxx/m, erit LC ∞ 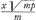nimirum si habeatur + OX quo casu praeter constructionem novissimam adhuc producenda est ZX versus Y, ut XY sit ∞ m, et ducenda YC parallela XI, eaque erit locus puncti quaesiti. Si vero habeatur - OX &c.

33.	Qua ratione hoc latus rectum oz/a et linea IN amm/oz inventa sit explicare operaepraetium videtur.

1) Les corrections de ces deux pages 304 et 305 ont rapport à l'ouvrage cité dans la Lettre N^o. 150. Note 1.

2) On lit en marge: haec omittamus [Chr. Huygens].

[p. 305]

pag.57.0.	Brevior adhuc est constructio, si tantum ex G ducatur perpendicularis super LG, ea enim secans lineam LH, ostendit punctum H per quod transire linea debet quaesita.
59.	E regione figurae in margine. Secunda haec ovalis uno casu est circulus perfectus cum nimirum FA ad AG rationem habet eandem quam 5 A ad A6, Unde certum est radios lucis ad punctum aliquod tendentes ope superficiei sphaericae ad datum aliud punctum omnes accurate cogi posse. Et hoc apertius in Dioptricis nostris demonstratum est.
64.	lin: 11. ad illa verba, Praeterquam versus A ubi paululum concava existit hoc notavi. Imo etiam versus A convexa erit quoties HA ad AF minorem rationem habebit quam A5 ad A6.
73.	l: 13. Legendum modo illa aut plana sit, aut à sectionibus Conicis aut Circuli effecta.
134.	l: 24. in margine notavi. Quoties terminus n/z x in aequatione non reperitur certum est etiam in terminis qui lineam IN, rectumque et transversum latus exprimunt deleri debere a et z; hae enim non existunt, nisi cum ducitur IL ut apparet ex constructione pagg: 31 et 32. Cum autem loco termini n/z x habetur x absque adjuncta fractione, oportet sumere KL ∞ IK, vel AB, est enim quasi z ipsi n aequalis foret. In terminis autem qui lineam IN, et rectum et transversum latus exprimunt, retinendae sunt z et a, earumque loco quaelibet duae lineae sumi possunt quae ad se invicem rationem servent IK ad KL.
139.	lin. 9. lege, neque enim hic habetura. lin. sequente, lege supponitur, cum nulla ipsi xx fractio adhaereat. lin. 12, dele, - ox. lin. 13. repone o/z.
135.	l: 3. lege B ∞ y.
136.	l: 9 xx nec reperitur m aut n/z x, lege xx. Non reperitur autem m, aut n/z x;
43.	l: 25 lege praecedenti non esse simpliciorem.
203. l: 28 post illa verba, quae rursus perpendiculari BD sit aequalis vellem subjungeres ista. Oportet autem perpendicularem quae ducitur in latus subtensum angulo intra quem punctum sumptum est, auferre ex summa duarum reliquarum. Quod autem de inordinatis figuris addidisti omnino suadeo ut omittas nam ne quidem in triangulo inordinato verum est.
289.	Hoc annotavi. Potest etiam fieri ut tres hae, DE, CB, NM inter se aequales sint atque in unam rectam conveniant, quae tertia pars erit rectae HI. Quo casu hoc animadversione dignum est, quod in puncto eo quo circulus Parabolam secat, eadem tamen linea recta et circulum et Parabolam contingat.

[p. 306]

In DIOPTR. latin:²⁾

pag. 303.	6, pro major legendum est minor. nam minor est ratio 187 ad 250 quam 3 ad 4. Sed sic quoque error corrigi posset et melius meo judicio, ut major retineatur, et legatur, major est quam quatuor ad tria et paulo post, invenio esse ut 250 ad 187.
193.	Si tantum ex P super BP perpendicularis ducatur ea abscindet ex BI partem versus I quae ad IP proportionem habebit quae refractionem metitur.
152.	in fine, an bruta ratione praedita.^3)
157.	in fine, quid manus Dei?
164.	9 canticus.
171.	16 Aborigines.
188.	interminata.
204.	margine, et 361. 3 quo me communicavit. ibid: l. 5 a fine, sistendum.
211.	circa finem, fama, potius solent.
120.	μυθιϰὸν. ἡρωιϰὸν.
239.	lin. 6. solertissimus datus.
240.	5. proluerunt.
241.	quid sol in aequatore constitutus; circa finem paginae De Sphaerae constructione intelligendum.
243.	9 sed ad partes meridiani easdem habitantes. non capio, tum quod sequitur.
247.	2 commentae.
248.	10 odium.
249.	13 conjectae.
252.	circa finem, λαμπρὸς.
272.	10 caliginoso tanto.
286.	2 promus.
289.	6 at ne quid.
301.	10 superficia.
310.	10 a fine, imaginoso.
321.	17 proletarium.
325.	11 intentatur.
341.	de stellarum et arenae numero, de duplici aeternitate.
359.	12 progenies, exculperit.
362.	7 à fine, adventores.
366.	1 in mortario pensitaret. Salvet.
414.	15 pererrandum.
432.	12 pateretur.
438.	11 fulgur. hoc.
443.	10 regnare antecessoribus. idem 444. 5.

2) Ces deux corrections ont rapport à l'édition de la Lettre N^o. 161. Note 2.

3) Nous n'avons pu trouver à quelle édition ces corrections se rapportent.