Oeuvres complètes. Tome I. Correspondance 1638-1656

[p. 237]

N^o 161.
Christiaan Huygens à G.A. Kinner A Löwenthurn.
9 août 1653.

La minute et la copie se trouvent à Leiden, coll. Huygens.
La lettre est la réponse au No. 160. Kinner à Löwenthurn y répondit par le No. 162.

Generosissimo Clarissimoque Domino Domino M.¹⁾ A. Kinnero a Löwenthurn. Chr. Hugenius S.D.

Literis meis tandem receptis omnem tibi sinistram de me opinionem exemptam libentissime cognovi; ubi autem tanto tempore delituerint equidem excogitare nequeo, nam Patrem Gregorium cui ipsas commendaveram non ausim tantae negligentiae reum facere. Invaletudo mea ex febri tertianâ quâ quadrimestri spatio continuò exagitatus fui, in causâ est quo minus apud ipsum inquisiverim, cum super ista re, tum super dissidio nostro et promissa causae suae defensione quam nullam adhuc prodijsse demiror. quoniam jam dudum perscriptam à quodam Patre Ainscomio mihi relatum fuit. Rogo ne similiter nobis invideas propositiones istas 35 quibus secundam Quadraturam ordinasse te et intelligibilem probabilemque reddidisse scribis, quod mihi vix fit verisimile. Absit tamen ut Patrem Gregorium in errore versari pro axiomate statuam ut mihi imputare videris; nam id ea tenus mihi persuasi tantum quatenus evidenti demonstratione pervicisse credidi. quodcunque autem demonstrare intendimus, id axiomatis loco non haberi manifestum est. De caetero Cyclometra nostro Vietam à te postponi Inventionum splendore non mirum est quandiu quadraturae legitimam demonstrationem inter illius inventa computas, ea vero seposita si perseveras, liceat mihi à te dissentire. Vix intelligo qui fieri possit ut Dioptrica solum²⁾ Cartesij videris, Geometriam non videris, quae tamen utraque simul olim prodiere, veruntamen lingua Gallica.³⁾ Sed Geometriam quoque jam quatuor ab hinc annis latinam fecit Fr. Schotenius⁴⁾ Professor lugdunobatavus, à quo Algebram istam literariam primum edoctus fui, cujus nunc cognitione nihil aequè carum habeo. Hanc si teneas cogitesque à Vieta et Marino Getaldo⁵⁾ resuscitatam fuisse, et à Cartesio plenissimè restitutam (nam talem quoque veteribus Geometris in usu fuisse certissimis mihi indicijs constat) tum demum merita laude

1) Lisez: G.

2) R. Cartesius, Specimina philosophiae. Dissertatio de methodo recte regendae rationis, Dioptricae et Meteora. ex gallico latine versa et ab authore emendata. Amst. Ludov. Elsevirius 1644. in-4^o. On dit que le traducteur en est Estienne de Courcelles.

3) Voir la Lettre N^o. 5. Note 7.

4) Voir la Lettre N^o. 150. Note 1.

5) Marino Ghetaldi naquit en 1566 à Raguse et mourut en 1627. Il était noble Italien et vers la fin de sa vie ambassadeur de Venise auprès du Pape. Il nous a laissé plusieurs écrits sur les anciens mathématiciens.

[p. 238]

horum virorum labores ingeniumque celebres. Dioptrica uni Cartesio debet quod circa refractionis naturam certo gaudet principio sine quo cum Iridis miraculum explicari nequeat, non est putandum Marcum Antonium de Dominis aut alium quenquam, laudem ipsi pulcherrimae hujus speculationis praeripuisse. In tractatu meo dioptrico regulas tradidi quibus de Iride doctrina perficitur. Unam quae datâ proportione refractionis (scis quorum sinuum rationem designem) expeditè computare docet angulum sub quo iris cerni debeat. aliam quae hoc angulo dato proportionem illam exhibet, quam vel maximè utilem inveni ad inveniendam exactissime in vitro et alia quavis pellucente materia refractionis quantitatem, paratis ad hoc ex quaque materia cylindrulis sphaerulisve, solique expositis atque ita notato angulo sub quo iris in vitrea aliave pluvia conspici deberet. Verum haec ex tractatu ipso quandoque te percepturum planius spero, nunc demonstrationem hic scribam constructionis



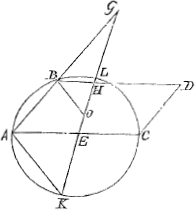duarum mediarum proportionalium quam desideras⁶⁾ Perficiatur circulus ALCK et producatur GE usque ad circumferentiam in K, Et jungatur AK, eique parallela ducatur BO. Itaque similes sunt Δli AEK, BHO; et quia AE aequalis EK, etiam BH aequalis HO: sed et HG, HD ex constructione inter se aequales sunt, igitur tota OG aequalis BD, hoc est diametro AC vel LK. Et ablata communi LO relinquuntur aequales inter se GL et OK. Est autem ▭ KGL aequale ▭ lo AGB, ideoque ut KG ad GA ita BG ad GL. Verum ut KG ad GA ita propter triangulos similes est quoque OG ad GB et ita reliqua etiam OK, cui aequalis LG ad BA reliquam. Ergo ut OG hoc est AC ad GB ita GB ad BL⁷⁾, et LG ad BA. Patetque inter AC et AB lineas medias esse BG et GL quod erat demonstrandum.

Trisectionis anguli quam ad me misisti constructio manifestam rationem habet ijs, qui Cartesij Geometriam legerunt, quae simul docet quam sit utilis contemplatio dictae partitionis ad solidorum problematum compositionem. Potest vero ad compositionem quoque adhiberi, sicut sequenti exemplo intelliges, neque enim possum quin hac occasione pulcherrimam Tibi constructionem adscribam Problematis Archimedei, qua inventa non leviter me gavisum memini. Problema est, Sphaeram propositam plano secare secundum datam rationem. Et Archimedis quidem compositio deperijt nisi illa est quam Eutocius in vetusto quodam libro se reperisse testatur. At Dionysidorus aliam invenit aliamque Diocles. Sed Pater Gregorius hisce meam praeferebat, quam ipsi olim cum demonstrationi miseram eo quod per parabolam et circulum absolvebatur. Caeterum hanc quae nunc sequitur deinceps inveni.

6) Voyez à ce sujet la Lettre N^o. 146.

7) Lisez: GL.

[p. 239]

Proponatur sphaera, et maximus in ea sit circulus AKCL, diameter AC, centrum M, proportio verò data sit S majoris ad T minorem.

Dividatur AC in E ut sit sicut S ad T ita AE ad EC, et accommodetur in circulo ABCD recta AR aequalis differentiae duarum AE, EC. Et ei quae subtendit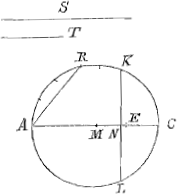



tertiam partem arcus AR, sumatur aequalis MN; Tum si ducatur per N planum KL quod diametro AC sit ad angulos rectos; Dico hoc sphaeram sic secare, ut portio KAL sit ad portionem KCL ut S ad T.

Demonstratio cum ijs quae ad ipsam spectant, epistola⁸⁾ hanc aequat propemodum, et Tu ulteriori contemplatione onerandus non videris. Itaque finem hic faciam hoc unum te obtestatus, ut sive ipse quid novae rei speculatus fueris sive è Geometris aliquis quibuscum isthic versaris ne mihi voluptarem deneges talibus perfruendi. Vale.

9 Aug. 1653.

Perillustri et Generoso Domino Domino M. Godefr. Aloysio Kinnero a Löwenthurn.

Pragam.

8) Lisez: epistolam (ā).