Oeuvres complètes. Tome I. Correspondance 1638-1656
(1888)–Christiaan Huygens–No 162.
| |
[pagina 240]
| |
timè constantīs tenor, et maximè rerum mathematicarum memoria, quae aliàs ingratissimi solent esse valetudinis affectae comites, iam poenè persuadent, te incolumitati pristinae, studijsque tibi charissimis plenè restitutum. A Patre Aynscom defensionem quadraturarum apparari, diu est quod ex eius ad me literis intellerimGa naar voetnoot1): ad tuum verò scriptum, nè specialius quid expectes; summum illud, quantum ego quidem conijcio, responsionis accipies, Te in finem alium, quàm Pater Gregorius in prima quadratura sua intendat, collimâsse. Ad me quod attinet, ita de Patris Gregorij inventionibus iudico, ut quamvis abesset inventi Tetragonismi felicitas, parum apud me de illarum aestimatione periturum existimem. Sunt enim complures in opere illo speculationes, tetragonismo fortasse non inferiores, quibus sua apud Geometras nequaquam periret aestimatio, nisi tot ab omnium saeculorum mathematicis adhibiti conatus quadraturam circuli prae caeteris inventis fecissent commendabilem. Progressiones Geometricae, proportionalitatum nova tractatio, Vngulae Cylindricae Cubatura, Symbolifatio Spiralis et Parabolae, ut taceam absolutam et facilem Conicorum doctrinam, satis apud omnes perorarent meam causam; nisi nescio quis nimium religiosus in veteres amor, aut ingenita dissentiendi cupiditas verum iudiciorum sensum suspenderent. Neque ita tamen Gregorij rebus afficior, ut aliquid Vietae caeterisque derogatum velim. Geometrica certè Vietae maiorem in modum me afficiunt, propter nitidam construendi methodum, tametsi non nihil in demonstrationibus desiderem de claritate. In Analyticis (ut ingenuè tibi confitear) usum non habeo, quoniam ea partium harum infelicitas est, ut paucos singularis eorum cognitio delectet. Ego certè iam pridem illa desidero, sed experientiâ forsitan ipse didicisti, quàm exigui sperari possint progressus apud eos, qui manuductore idoneo detentiGa naar voetnoot2) sunt. Eorundem Analyticorum amor maius in me desiderium facit Geometriae Cartesianae, in qua accuratius ea tractari asseris, quam esto hucusque videre non potui, facilè tamen eius valorem ex dioptrica conijcio. Jn qua nova circa refractiones principia non possum non commendare; cuius vestigijs si institeris, non dubito â Dioptrice tua, quam moliris, magnam in hac materia perfectionem expectari posse. Illud autem te vel maximè rogatum velim, nè omittas rationem aliquam idoneam è theorematis tuis elicere, cuius operâ mirabilem illam colorum, quae in iride et aliàs refractionem comitari solent, genesim planius intelligamus. Nam quod Cartesius eos et omnes omnino etiam permanentes colores produci asserit â nescio quo imaginario lucidarum particularum heterogeneo gyro, non placet, et magis est (pace tanti viri tuâque dixerim) confingere, quâm philosophari. Sed quando in refractionem incidimus, non possum non meminisse theorematis apud nos ante paucos annos multum exagitati, occasione thesium quarundam de JrideGa naar voetnoot3), quas Professor Matheseos Pa- | |
[pagina 241]
| |
ter Balthasar ConradusGa naar voetnoot4) proposuerat, in quibus eandem sententiam fuerat complexus, quam Des-Cartes, de cuius tamen vulgata Dioptrice nihil dum isthic audiveramus. Quandoquidem ergo tunc demonstrabatur iridem generari ope refractionis radiorum solarium factae in guttarum sphaerulis, venit in quaestionem, num etiam radij ê sole in guttam allapsi eamque tangentes refringantur perinde ac ij qui eandem
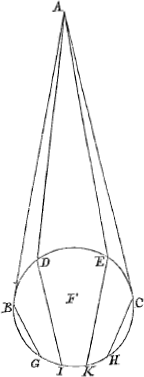 intersecant. Negabant mordicus universi tum praesentes, tum et multi ex ijs, quos idem Pater Conradus per literas consuluerat. Vnus ipse erat qui affirmabat, cuius rationem, quâ idipsum nitebatur demonstrare, subnectam, tuum ea super re iudicium intellecturus. Sit punctum aliquod solis A, â quo in sphaerulam BCDE incidant radij AB, AC tangentes eandem in punctis B, C; AD et AE verò sint secantes. Dico tangentes AB, AC etiam refringi. Cum enim propter medium guttae densius, quàm sit aër, fiat refractio radiorum ad perpendicularem, inclinabuntur omnes refracti radij versus centrum F, claudenturque terminis cadentibus intra sphaeram verbi gratia BG, CH. Dico terminos radiorum refractorum BG, CH oriri â tangentibus AB, AC. Sint enim radij AD, AE secantes sphaeram, quorum refracti sint DI, EK, hi non terminabunt omnes refractos; quia cum arcus BD, EC, qui tangentes inter et secantes interiacent, quantumvis parvi, in sententia mathematicorum sint in infinitum divisibiles, poterunt inter B et D, itemque inter E et C cadere infiniti alij radij secantes, qui in sphaeram refringantur, adeòque secantes AD, AE refracti in DI, EK non terminant spacium refractorum. Atque idem discursus valet pro omnibus alijs sphaeram secantibus. Cum ergo constet esse aliquem terminum radiorum intra sphaeram refractorum, et ille non possit oriri â secantibus, necesse est illum provenire â tangentibus. Radij ergo globulum tangentes refringuntur. Haec erant, quae praesentibus sufficere opinabar. Gratias interim tibi ago maximas, pro transmisso theoremate de sectione sphaerae, cuius nitor mirum me affecit, magisque placuisset, si veritatem illius adiunctâ demonstratione comprobasses, quam si deinceps non invideris, scito nihil esse, quod vicissim â me tibi possit denegari. Vale meique memor vive, expers turbarumGa naar voetnoot5), quae vestros inter et Anglos insurrexerunt, quae opto nè studijs tuis officiant; si de illarum successu certi subinde quid literis | |
[pagina 242]
| |
tuis breviter adiunxeris, me denuo ad plura obligabis obsequia, qui iam antè vivo et morior Perillustris ac Generosissimae Dominationis Tuae servus promptissimus Godefridus Aloysius Kinner â Löwenthurn. Manu Propriâ.
Dabam Pragae 3 Cal: Septembr: 1653. Perillustri, Generosissimo, Clarissimoque Domino, Christiano Hugenio etc. Domino mihi Colendissimo, Observandissimoque. 6. Hagam Comitis. S Graven Hage. |
|

