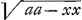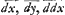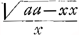Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–No 2713.
| |
[pagina 198]
| |
Porro data proprietate tangentium lineae curvae quaesitae, solet dari vel haberi aequatio exprimens relationem inter BT subtangentialem et AB vel BG abscissam vel ordinatam, aut ambas simul. Vocemus subtangentialem ipsam BT, partem
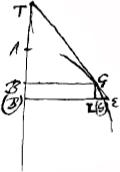 Axis cadentem inter ordinatam BG et tangentem GT. Itaque, si AB vocetur x et BG y, et BT t, res redibit ad aequationem quam ex indeterminatis solae ingredientur x, y, t. Quo facto quaeritur aequatio, quam sublata t, duae tantum indeterminatae x et y ingrediantur. Ita ex data proprietate tangentium habebitur curvae constructio. Ex aequationibus autem illis, quae exprimunt relationem ipsius t ad reliquas eligamus illas simpliciores in quibus valor ipsius t per x et y habetur purè; ut si sit 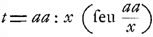 vel t=ax:y, vel t=y vel t=ax:y, vel t=y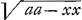 , vel t=yy , vel t=yy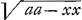 :ax, aliisque modis infinitis. Itaque id nunc agitur ut ex dato valore subtangentialis per abscissam, vel ordinatam, vel ambas, detur aequatio exprimens relationem inter ordinatam et abscissam. :ax, aliisque modis infinitis. Itaque id nunc agitur ut ex dato valore subtangentialis per abscissam, vel ordinatam, vel ambas, detur aequatio exprimens relationem inter ordinatam et abscissam.
Habeo autem diversas vias, quibus magnum hoc problema in oblatis casibus aggredior. Sed hanc optimam esse judico, (quoties ea uti licet) ut problema tangentium inversum revocetur ad Quadraturas. Analysis enim duorum est generum, una per saltum, cum problema propositum resolvimus ad prima usque postulata; altera per gradus, cum problema propositum reducimus ad aliud facilius. Et quia saepè fit, ut prior Methodus prolixis nimis calculis indigeat, confugiendum est non raro ad secundam; tametsi enim prior sit absolutior nec aliis indigeat praecognitis, commodior tamen est posterior, quia laborem minuit, jam inventis utendo. Ut verò intelligatur, quomodo persaepe Problema tangentium inversum ad Quadraturas revocari nullo negotio possit, dicendum est aliquid de quodam calculi genere a me introducto, notisque novis in eo adhibitis; ita enim efficio, ut multa primo obtutu appareant, et ipso calculi lusu nascantur, quae alias vi ingenii aut labore imaginationis assequi necesse est. Nec aliam ego causam video cur Clmus Fatius, qui jam dudum praeclara ingenii specimina nobis deditGa naar voetnoot3), haeserit ubi irrationales subtangentialis valorem ingrediuntur, velut in casu per celeberrimum Hugenium mihi proposito, ubi t=yy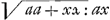 :axGa naar voetnoot4), quam quod hujusmodi expressio non aeque calculo analytico apta est, ac mea, per quem ipsius t relatio ad y et x aliquo modo generali exprimitur. Ita enim judico, cum mens humana ad cogitandum notis indigeat, eo posse nos ratiocinari melius, quo magis notae ipsae exprimunt rerum relationes. :axGa naar voetnoot4), quam quod hujusmodi expressio non aeque calculo analytico apta est, ac mea, per quem ipsius t relatio ad y et x aliquo modo generali exprimitur. Ita enim judico, cum mens humana ad cogitandum notis indigeat, eo posse nos ratiocinari melius, quo magis notae ipsae exprimunt rerum relationes.
| |
[pagina 199]
| |
Consideravi igitur tàm abscissas quam ordinatas habere elementa quaedam momentanea, seu differentias indefinite parvas; et elementum abscissae esse ad elementum ordinatae, ut subtangentialis est ad ordinatam. Nam si cogitemus punctum mobile B ex fixo A egrediens percurrere axem AB (B), et adeo abscissas AB nihil aliud esse quam distantias puncti B mobilis à puncto fixo A patet incrementa abscissarum momentanea B (B) esse ut velocitates, quas punctum B in quovis Axis loco, aut quovis temporis momento habet, adeoque inassignabilis parvitatis, et similiter se rem habere cum ipsis GLGa naar voetnoot5) incrementis ordinatarum, seu excessu ordinatae (B) (G) super proximè (id est inassignabili intervallo) praecedentem BG. Haec incrementa, aut (si contrarium motum fingas) decrementa, vel, ut generalius loquamur, elementa ordinatarum vel abscissarum, aut (si malis) differentias inassignabiles (quarum tamen ad alteras omninò assignabilis est ratio) notis designare volui, exprimentibus relationem ad id cujus sunt differentiae; itaque quia abscissas AB vocavimus x, et ordinatas BCGa naar voetnoot6), y, elementa abscissarum seu differentias minimas B (B) vocabimus dxGa naar voetnoot7); et elementa ordinatarum, seu differentias minimas GLGa naar voetnoot5) vocabimus dy. Possemus ipsas dx vel dy peculiaribus exprimere literis, ut e, v, vel ut lubet, sed ita non appareret relatio ad x et y, quae tamen ipsis notis expressa plurimum juvat, modumque dedit mihi curvas transcendentes exprimendi per aequationes finitas non alias adhibendo indefinitas, quam x et y, et harum affectiones inter quas non tantum potentias aut (his reciprocis) radices, ut x2, √x, etc. sed et differentias et (his reciprocas) summas refero, harumque notas ad supplendum calculum promovendamque ad Transcendentes Analysin omnino aptas judico. Et quemadmodum non optimè faceret qui pro x2, x3 etc., semper vellet adhibere literas, e, v, ad evitandum hoc notationis genus, licet admoneret se per e et v quadratum aut cubum intelligere, ita similiter praestat saepe dx aut ddx (differentiam aut differentiam differentiarum ipsarum x) adhibere, quam pro ipsis uti literis e aut v vel similibus. Sic Cycloidem exprimo per hanc aequationemGa naar voetnoot8)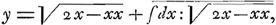 , posito radium circuli generatoris esse 1, et x esse abscissam in axe inde à vertice, et y esse ordinatam ad axem, et dx esse incrementa abscissarum, et , posito radium circuli generatoris esse 1, et x esse abscissam in axe inde à vertice, et y esse ordinatam ad axem, et dx esse incrementa abscissarum, et 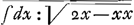 esse summam omnium dx:√2x-xx, seu quantitatem cujus differentialis est ad differentialem abscissae ut radius ad sinum, quae summa vel quantitas revera est arcus. Et hinc facillimo calculo sine ullo figurae respectu derivatur proprietas tangentium Cycloidis nota, quae nostro modo expressa ita habet, esse summam omnium dx:√2x-xx, seu quantitatem cujus differentialis est ad differentialem abscissae ut radius ad sinum, quae summa vel quantitas revera est arcus. Et hinc facillimo calculo sine ullo figurae respectu derivatur proprietas tangentium Cycloidis nota, quae nostro modo expressa ita habet, 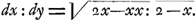 . Caeteraque . Caeteraque
| |
[pagina 200]
| |
omnia circa Cycloidem inventa pluraque alia similiter ex tali calculo analytice derivantur.  Sed ut nostrum institutum prosequamur. Producatur (B) (G) dum tangenti TG itidem productae occurrat in E, constat puncta (G) et E haberi posse pro coincidentibus, seu rectam (G) G, quae jungat duo curvae puncta inassignabiliter distantia, productam esse ipsam curvae tangentem. Cum dudum ab aliis explicatum sit, rectam quae curvam secat in duobus punctis, transire in tangentem eo casu, quo duo sectionis puncta coincidunt. Itaque EL non minus quam (G) L poterit vocari dy, et ob triangula TBG et GLE similia fiet TB ad BG, ut GL ad LE, seu t:y∷dx:dy, idque ipsum est quod diximus subtangentialem t, esse ad ordinatam y ut dx elementum abscissae ad dy elementum ordinatae, et quia proinde t:y=dx:dy, fiet t=y dx:dy, qui est generalis valor subtangentialis. Et hunc conjungendo cum speciali valore quem natura problematis offert, pervenitur ad aequationem differentialem, quam ubi convertere licet in summatricem puram, habetur reductio problematis tangentium inversi ad Quadraturas. Quae reductio ut intelligatur melius, ostendam (quod momenti est maximi): Quandocunque proprietas tangentium data exhibet valorem subtangentialis per solam (ex indeterminatis) abscissam vel solam ordinatam, problema reducitur aa Quadraturas. Ponamus enim t dari par x, utique quia t=y dx:dy, fiet dy:y==dx:t, adeoque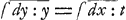 . Jam . Jam 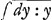 pendet ex quadratura Hyperbolae, et pendet ex quadratura Hyperbolae, et 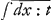 etiam pendet ex aliqua quadratura ejus nempe figurae cujus ordinata est 1:t, posito nempe pro t poni ejus valorem per x itaque res reducta est ad quadraturas. Exempli causa, si esset t=1:x, sieret etiam pendet ex aliqua quadratura ejus nempe figurae cujus ordinata est 1:t, posito nempe pro t poni ejus valorem per x itaque res reducta est ad quadraturas. Exempli causa, si esset t=1:x, sieret 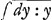 =∫xdx=½xx; et ita curva proposita habetur ex quadratura Hyperbolae. Si esset t=1: =∫xdx=½xx; et ita curva proposita habetur ex quadratura Hyperbolae. Si esset t=1: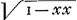 , sieret , sieret 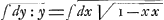 , atque ita curva quaesita haberetur ex supposita quadratura tam circuli quam hyperbolae.
Similiter si t detur per y, quia t=ydx:dy, siet dx=dy t:y adeoque x= , atque ita curva quaesita haberetur ex supposita quadratura tam circuli quam hyperbolae.
Similiter si t detur per y, quia t=ydx:dy, siet dx=dy t:y adeoque x=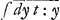 . Quod si jam ex problemate detur valor ipsius t per y, intelligi poterit cujusnam figurae quadratura sit opus: nam ponamus esse t=y, fiet x=∫dy id est x=y, et linea quaesita est recta. Si sit t=yy, fiet x= . Quod si jam ex problemate detur valor ipsius t per y, intelligi poterit cujusnam figurae quadratura sit opus: nam ponamus esse t=y, fiet x=∫dy id est x=y, et linea quaesita est recta. Si sit t=yy, fiet x=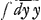 seu x=yy:2, et linea quaesita est Parabola. Si t=y3, fiet x=∫dy yy; seu x=y3:3 et linea est parabola cubica. Si t sit constans, verb. gr. si t=1, fiet x= seu x=yy:2, et linea quaesita est Parabola. Si t=y3, fiet x=∫dy yy; seu x=y3:3 et linea est parabola cubica. Si t sit constans, verb. gr. si t=1, fiet x=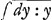 , adeoque linea quaesita pendet ex quadratura Hyperbolae. Si t sit irrationalis, res itidem procedet, nam si ponatur t=y√1-yy, fiet x= , adeoque linea quaesita pendet ex quadratura Hyperbolae. Si t sit irrationalis, res itidem procedet, nam si ponatur t=y√1-yy, fiet x=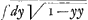 , adeoque linea quaesita pendet ex quadratura CirculiGa naar voetnoot9). , adeoque linea quaesita pendet ex quadratura CirculiGa naar voetnoot9).
| |
[pagina 201]
| |
Sed si valor ipsius t detur per x et y simul, tunc non semper facile est problema reducere ad Quadraturas, infiniti tamen sunt casus ubi res procedit. Et generaliter hoc pronuntiari potest: Quandocunque valor subtangentialis t est productum ex duabus quantitatibus seu formulis, quarum una datur per solam (indeterminatarum) abscissam x, altera per solam (indeterminatarum) ordinatam y, tunc problema reducitur ad quadraturas. Exempli causa. Si sit t=xy, seu factum ex x in y; fiet xy=ydx:dy, seu dy=dx:x, seu y=∫ 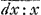 , quod pendet ex quadratura Hyperbolae. Si sit t=y:x seu factum ex y in 1:x, fiet y:x=ydx:dy, seu dy=xdx, seu y=∫ , quod pendet ex quadratura Hyperbolae. Si sit t=y:x seu factum ex y in 1:x, fiet y:x=ydx:dy, seu dy=xdx, seu y=∫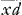 x, seu y=xx:2, quae est aequatio ad Parabolam. Si sit t=x:y seu factum ex x in 1:y, fiet x:y=ydx:dy, seu xdy=yydx seu dy:yy=dx:x, seu x, seu y=xx:2, quae est aequatio ad Parabolam. Si sit t=x:y seu factum ex x in 1:y, fiet x:y=ydx:dy, seu xdy=yydx seu dy:yy=dx:x, seu 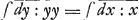 , quae datur ex quadratura Hyperbolae, nam
∫dy:yy datur absoluteGa naar einda) nihil aliud enim est quam quadratura Hyperboloidis secundi gradus. Sic si t=y: , quae datur ex quadratura Hyperbolae, nam
∫dy:yy datur absoluteGa naar einda) nihil aliud enim est quam quadratura Hyperboloidis secundi gradus. Sic si t=y: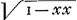 , seu factum ex y in 1: , seu factum ex y in 1: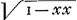 , fiet y: , fiet y: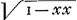 =ydx:dy, seu fiet dy=dx =ydx:dy, seu fiet dy=dx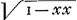 seu y= seu y=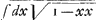 , quae pendet ex quadratura circuliGa naar eindb).
Ad hanc jam classem revocatur et curva mihi proposita, cujus subtangentialis rectae valor praescriptus erat t=yy , quae pendet ex quadratura circuliGa naar eindb).
Ad hanc jam classem revocatur et curva mihi proposita, cujus subtangentialis rectae valor praescriptus erat t=yy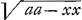 :ax(1)Ga naar eindc). Nam quia semper est t=ydx:dy (2) fiet y :ax(1)Ga naar eindc). Nam quia semper est t=ydx:dy (2) fiet y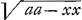 :√dx:dy (3) per (1) et (2). Sit a=1(4). Ergo ex (3) et (4) fiet ydy=dx x: :√dx:dy (3) per (1) et (2). Sit a=1(4). Ergo ex (3) et (4) fiet ydy=dx x: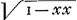 . (5) et acquationem (5) utrinque summando, quia ∫ydy=yy:2 (6) fiet per (5) et (6) . (5) et acquationem (5) utrinque summando, quia ∫ydy=yy:2 (6) fiet per (5) et (6)  (7). Id est, opus est tantum ut reperiatur quadratura generalis, seu indefinita, figurae cujus ordinata est x: (7). Id est, opus est tantum ut reperiatur quadratura generalis, seu indefinita, figurae cujus ordinata est x: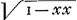 , abscissa existente x. Haec autem quadratura habetur absolutè. Nimirum x: , abscissa existente x. Haec autem quadratura habetur absolutè. Nimirum x: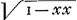 vocetur Z (8). Jam centro A radio AK, qui vocetur Z (8). Jam centro A radio AK, qui
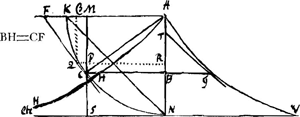 sit a vel 1, describatur circulus, in cujus circumferentia sumto arcu LCGa naar voetnoot10), et x seu AB sumta in normali ad AK, quae sit arcus sinui aequalis, jungatur radius AC et tangens arcus CF, ipsi AK productae occurrens in F, erit Z. Nam ob triangula similia CBA et ACF, fiet Z seu FC ad AC seu 1, ut AB seu x ad BC seu 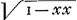 ; unde Z seu FC est x: ; unde Z seu FC est x: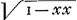 , ut jubet aequatio (8). Si ergo FC translata in BH ordinatim applicetur ad AB angulo recto ut fiat linea curva AHH, habebitur figura ABHA, per cujus quadraturam reperietur quaesita y. , ut jubet aequatio (8). Si ergo FC translata in BH ordinatim applicetur ad AB angulo recto ut fiat linea curva AHH, habebitur figura ABHA, per cujus quadraturam reperietur quaesita y.
Porro ex C in AK agatur normalis CM, ajo rectangulum MKA aequari trilineo | |
[pagina 202]
| |
ABHA, adeoque infinitum spatium AN etc. HA aequari quadrato radii. Quod sic ostendo: per punctum Q in CF indefinitè vicinum ipsi C, agatur in CM et AB normalis QPR, et alia Qβ normalis ad AK; et MC producatur in S, ut sit MS aequ. AK radio; et ob triangula CPQ et ACF similia, fiet AC:CF∷CP:PQ, seu AC in PQ=CF in CP. Jam est AC in PQ=SM in Mβ, et CF in CP=HB in BR; ergo SM in Mβ=HB in BR, adeoque et summa omnium rectangulorum SM in Mβ, id est rectang. SMK aequatur summae omnium rectangulorum HB in BR, seu areae ABHA, quod asserebatur. Habetur ergo quadratura proposita. Hinc jam constructionem lineae quaesitae ita ducemus. Area ABHA seu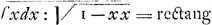 . SMK seu 1- . SMK seu 1-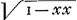 (9). Ergo ex aeq. (7) per (9) fit yy:2=1- (9). Ergo ex aeq. (7) per (9) fit yy:2=1-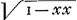 (10), quae aequatio est ad curvam quaesitam. Unde si tollamus irrationalitatem, fiet y4:4-yy+1=1-xx, (11) et ad supplendos gradus ex lege homogeneorum, pro 1 restituendo a fiet y4=4aayy-4aaxxGa naar voetnoot11) (12). Constructio autem erit talis. Inter duplam MK et radium AK sumatur Media proportionalis, quae erit y quaesita (ex aeq. 10) eique aequalis BG ordinatim applicata ad AB angulo recto, dabit curvam AGV quaesitam, cujus ultima ordinata NV aequabitur rectae KN seu lateri quadrati circulo inscripti. Et in hac linea, si sit AB, x et BG, y et AN, a tunc subtangentialis BT, seu t, erit yy (10), quae aequatio est ad curvam quaesitam. Unde si tollamus irrationalitatem, fiet y4:4-yy+1=1-xx, (11) et ad supplendos gradus ex lege homogeneorum, pro 1 restituendo a fiet y4=4aayy-4aaxxGa naar voetnoot11) (12). Constructio autem erit talis. Inter duplam MK et radium AK sumatur Media proportionalis, quae erit y quaesita (ex aeq. 10) eique aequalis BG ordinatim applicata ad AB angulo recto, dabit curvam AGV quaesitam, cujus ultima ordinata NV aequabitur rectae KN seu lateri quadrati circulo inscripti. Et in hac linea, si sit AB, x et BG, y et AN, a tunc subtangentialis BT, seu t, erit yy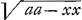 :ax, ut desiderabatur. :ax, ut desiderabatur. |
|