Oeuvres complètes. Tome IV. Correspondance 1662-1663

[p. 246]

N^o 1068.
R.F. de Sluse à [Christiaan Huygens].
6 octobre 1662.

La lettre se trouve à Leiden, coll. Huygens.
Elle est la réponse au No. 1065.

Nobilissime Domine

Recté conjecistj methodum meam tangentium ad omnes curuarum species producj, quarum proprietas, duarum, vt solet, quantitatum ignotarum, cum ijs quae notae sunt, implexarum, equatione exprimitur. Jgitur ad hanc quoque Schotenij quam proponis, cuius aequatio est x³+y³-n y x ‖ o¹⁾ positâ scilicet AB aequali n, AI y, IL x. Ecce enim tangentem in puncto L breuissimo calculo repertam, et qui lineam integram non impleat. Productâ BA in E ita ut AE sit subtripla AB,



fiat vt differentia quadratj AI et rectanguli AE, IL, ad differentiam rectanguli EAI, et quadrati IL, ita LI, ad ID, iuncta enim LD tanget curuam in L. Ex hac constructione satis apparet aliquot casus esse considerandos circa punctum datum. Si enim daretur punctum F, ex quo demissâ normali FG, rectangulum sub AE, FG, aequale esset quadrato AG (quod punctum esse ad parabolam cuius axis est normalis AO, vertex A, latus rectum AE, euidens est) tunc ex puncto F ducta parallela ipsj AB tangeret curuam in F. At si daretur punctum H, ex quo demissâ normali HK, rectangulum EAK, aequale esset quadrato KH (quod punctum rursus esse ad parabolam cuius axis AB, vertex A, latus rectum AE, satis constat) tunc ipsa HK tangeret curuam in H. Demum si punctum datum L caderet inter F et H, punctum D, non vt prius versus A, sed ad partes B sumendum esset: quae omnia solâ aequationis contemplatione innotescunt. Recté interim obseruastj curuas huiusmodj commodiorem aliam aequationem recipere: sed pro ducendâ tangente quaelibet mihi sufficit. Vt ecce in curuâ quam his diebus literarum tuarum occasione

1) L'égalité est indiquée ici par le signe ‖.

[p. 247]

mihi finxi. Duae sunt ad rectos EA, AC, haec alterius subdupla, inter illas



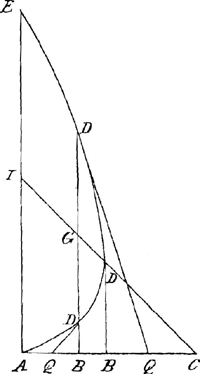vero curua est ADDE, cuius proprietas, vt applicatâ qualibet parallelâ EA, quae sit DDB, si AB vocetur y, BD x, AC n, fiat semper 2nx - xx - yy - 2xy ‖ o. Huius tangentem sic reperio in D puncto. diuisa EA bifariam in I, et iunctâ CI, secante DD in G, faciendum est vt vtraque AB, BD²⁾, ad DG, ita DB, ad BQ, iuncta enim QD tanget curuam in D: hoc tantum discrimine, quod si D sit in parte inferiori, Q cadet ad partes A, si vero in superiori ad partes C: at si punctum D sit in recta CI, tunc ipsa DB erit tangens. Ex quâ methodo infinitae curuarum proprietates reperiri possunt; referendo scilicet ad diuersas rectas, et ex aequatione qualibet ducendo tangentem. Eodem modo quo in hoc exemplo noua parabolae proprietas eruitur, nam hanc esse parabolam facile peruidebis. Occurrunt etiam leuj negotio puncta flexus contrarij in ijs curuis quae ad diuersas partes inclinantur, vt in Conchoide (in quâ mihi ingeniose praeiuisti³⁾) quam vnicâ parabola in vtroque^a) flexu secarj ostendj. immo quod amplius est, in conchoidibus infinitis, quae ex codem polo et circa eandem asymptoton describi possunt, reperi omnia puncta flexus ipsarum esse in eadem parabola quadrato=cubicâ. Similiter et in aliâ Conchoide a me excogitatâ, in qua scilicet recta quae a polo ducitur ad curuam, ita secatur ab asymptoto, vt rectangulum ex partibus sit semper eidem plano aequale, reperj tangentem et punctum flexus absque loco solido: et si eodem polo circa eandem asymptoton infiniter describj intelligantur, ostendj puncta flexus omnium esse in vnâ infinita Cissoide. Sed haec hactenus.

Venio nunc ad ea quae acute in curua Gutiscouij nostri obseruasti. ac dimensio quidem spatij infinitj statim occurrit artificio Roberuallij⁴⁾ vel alterius Geometrae ex Galliâ (inde enim nobis olim Romam missum recordor) quo etiam vt opinor vsus es; calix vero ille infinitae capacitatis, totus tuus est. quamuis enim multos

2) De Sluse veut dire la somme AB+BD.

3) Dans les ‘Problematum quorundam illustrium Constructiones’ (voir la Lettre N^o. 191, note 1), Christiaan Huygens s'occupe du problème suivant: In conchoide linea invenire consinia flexus contrarii. Consultez aussi la Lettre N^o. 641.

a) Heuratius absque loco solido haec puncta invenit⁶⁾. [Chr. Huygens].

6) Voir la Lettre No. 641, note 6.

4) Consultez le Traité des indivisibles par M. de Roberval, imprimé plus tard dans les
Ouvrages de Mathematique de M. de Roberval. A Amsterdam, chez Pierre Mortier. mdccxxxvi. in-4^o.

[p. 248]

similes dari ostenderim, immò, quod mirabere si tibi non incidit, multa solida in finitae latitudinis aequalia finitis inuenerim, ad illum tamen tuum calicem non attenderam, sed tantum ad dimensionem solidj genitj ex spatij curuâ et applicatâ terminatj circa axem reuolutione, in quam non magno molimine incideram. sed haec non sunt tantj vt nos alio festinantes morarj debeant. Ad experimentum tuum intelligo, cuius causam qui peruidebit, nae ille mihi verè lynceus erit. Satis mihi erit aliquam εἰϰοτολογίαν examinj tuo subijcere, saltem vt hoc bonae voluntatis argumento a te similes obseruationes posthac eliciam. Ac primum assentior Nobilissimo Boilio, dum in experimento Torricellij, non ab aeris pondere sed ab eiusdem elatere aequilibrium deriuat. Itaque ad illius rationes te remitto; nisi forsitan addi possit, pressionem illam elasticam hoc ipsum esse quod grauitatem vocamus. Nam hanc non esse qualitatem physicam, vt in scholis existimant, suppono; prout et motum aut pressionem non nisi ab impellente producj. Quibus admissis, quid mirum sj aqua ab aere, tam interno, quam ambiente libera, non descendit? quid enim ipsam vrgebat? parum sane interest quid post exhaustum aerem remanere dicatur in vitro: nam quidquid tandem sit non impellere corpus sed impulsuj non obnitj ad summum videtur. Ratio vero cur aqua non purgata descendat, statim sese offert; ex aeris nempe spiras suas explicantis impulsu, cum primum a circumstantis pressione libertatem nactus est. Sed cur idem in Mercurio non accidit? Jdem plané euenturum arbitror, si tam facile ab ipso aer separari posset. Abundare enim aere hoc satis indicat, quod igne vel leuissimo euolans tot Chymicis ludos faciat. An non etiam hoc ex ipsius pondere consumatur? παραδοξότατον id inquies, pondus ab aere, a cuius mixtura leuitatem in corporibus scholae hactenus deduxerunt. Sed dicj posse videtur aeris spiras, quo magis implexae et, vt ita loquar, intortae sunt, eo potentius nitj vt se explicent; et hanc esse si non solam saltem non minimam causam grauitatis. Hinc etiam fortasse oleis chymicis pondus; nempe ab aeris spiris in materiâ illa, vt vocant, calcinatâ vehementius contortis: quâcumque tandem ratione in illam impellantur quam inuestigare huius loci non est. Multa praetereo quae commentj ἀσϑενειαν fulcire possent: haec indicasse contentus, vt disquiras, quo modo cum experimentis, quae plurima hac in re fieri possunt cohaereant. Verbulum tantum addo de tuis oscillationibus quibus lineae in physicis considerationibus neglectae, vsum tam praeclarum asseruistj. Hoc mihi memoriam refricuit effati illius Platonicj⁵⁾, γεωμετρίαν εἶναι θηρευτιϰὴν μόνον, ea vero quae venando adepta est, vsui, vt facis, adhibere, hoc demum philosophi munus esse. Perge igitur Speculationum Geometricarum, quae vulgo apud imperitos male audiunt, vtilitatem ostendere, meque crede, ex animo

Tui Obseruantissimum

Renatum Franciscum Slusium.

5) Les mots cités se trouvent dans: Plato, Sophistae, 219 E.

[p. 249]

Plurimam tibi salutem dico Clarissimi Gutiscovij nomine, quod vt facerem, me rogauit ante aliquot dies cum hic adesset. Vale.

Dabam Leodij vi Octobris .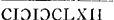

6) Voir la Lettre No. 641, note 6.