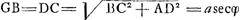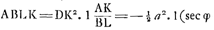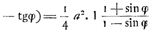Oeuvres complètes. Tome X. Correspondance 1691-1695

(1905)–Christiaan Huygens– rechtenstatus

N^o 2763.
Christiaan Huygens.
[décembre 1691].
AppendiceGa naar voetnoot1) au No. 2762.

La pièce se trouve à Leiden, coll. Huygens.

§ IGa naar voetnoot2).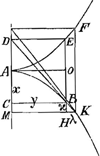

AC=x; CB=y; CD=z; BH=ϰ; HK=λ. AB est curva. AC recta; ad quam ordinatim applicata BC ad ang. rectos. BD est tangens in B, occurrens CA productae in D. Si compleatur ▭ BCDE erit punctum E ad curvam quandam AE, quae facit spatium BAE, aequale spatio BAC. Quod magni usus est.

BH:HK=DC:CB

ϰ:λ=z:y

ϰ/z=λ/y

xy=λz.

Spat. HC=spat. BEGa naar voetnoot3); unde et summae aequales, hoc est spat. KAF=spat. KAM; vel etiam BAE=BAC.

Hinc quadratura parabolae. Nam quia ibi est CD seu z=2x, fit AD=x; estque DE=y. Itaque AE est parabola eadem ac AB, cumque spat. AEB sit=ABC vel AED, erit ergo ABC=⅓ ▭ CE seu ⅔ ▭ⁱ CO ipsius CE dimidii.

[Spatium BAE circa axem DC facit duplum solidum ejus quod ex spat. ABC circa eundem axem, quia centr. gr. spatii FB duplo amplius distat ab AC, quam centr. gr. spat. HC]Ga naar voetnoot4).

§ IIGa naar voetnoot5).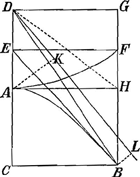

Hinc et dimensionem curvae, ex qua pendet constructio lineae Catenariae, reducere poteram ad quadraturam hyperbolae.

Sit enim ACGa naar voetnoot6) hyperbola aequilatera, cujus centrum D, axis DC applicata BC, tangens BE; et compleatur ▭ EAHF. Jam erit F punctum ad curvam quandam AF, quae facit spatium FAB=spatio hyperb^o ABC, unde spatium AFGD dabitur si à ▭^o CG auferatur duplum spatii hyperbolici ABC. Est autem curva AF ea ipsa cujus dimensione opus erat ad constructionem Catenariae, quandoquidem ducta AH parallela CB, proportionales sunt BG, HG, FG; propter proprietatem tangentis hyperbolae EB, quae invenitur faciendo proportionales DC, DA, DE. Curvam autem nostram ita construxeram, sumtis ubique proportionalibus BG, HG, FG vid. lib. G, pag. 20Ga naar voetnoot7).

PatetGa naar voetnoot8) ex jam dictis, ductâ recta DB, triangulum DCB ablato spatio hyp^o. ABC relinquere spatium DBA aequale dimidio spatii AFGD; est autem sp. DBA sector hyperb,^s aequalis spatio ABLK, ductis BL, AK ad asumptoton DL perpend^bus.

voetnoot1): Cet Appendice a été emprunté à la page 14 du livre H des Adversaria. Nous l'avons divisé en deux paragraphes.

voetnoot2): Démonstration d'un théorème général sur les quadratures.

voetnoot3): Lisez: BF.

voetnoot4): Cette remarque a été ajoutée après coup.

voetnoot5): Application du théorème du paragraphe précédent à la quadrature de la cour be xxyy=a⁴--aayy, dont dépend la construction point par point de la chaînette (DE=y; EF=x).

voetnoot6): Lisez: AB.

voetnoot7): Il s'agit du & VIII de la pièce N^o. 2625. Voir surtout la dernière phrase de ce paragraphe. En effet, les points B, H, F, G de notre figure correspondent aux points D, ϱ, φ et χ de la figure 5 de la pièce N^o. 2625.

voetnoot8): Ce qui va suivre a sans doute été ajouté pour pouvoir servir au calcul par logarithmes du rapport entre l'arc AK et l'abscisse LK (voir la fig. 4 de la pièce N^o. 2625) de la chaînette. En effet, d'après le & VIII cité, ce rapport égale celui de rectangle DH de la présente figure à l'aire ADGF=2×spat. ABLK, où HDA représente l'angle φ de la tangente à l'extrémité de l'arc avec la tangente horizontale du sommet. Posant A D=a, on a donc AH=atgφ; ; BL=½a√2 (secφ-tgφ); AK=½a√2, donc en appliquant la quadrature bien connue de l'hyperbole: spat. . d'où il suit pour le rapport cherché: 2 tg φ:1 1+sinφ/1-sinφ.