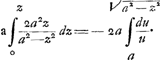Oeuvres complètes. Tome X. Correspondance 1691-1695

(1905)–Christiaan Huygens– rechtenstatus



[pagina 342]
N^o 2775. Le Marquis de l'Hospital à Christiaan Huygens. 23 novembre 1692. La lettre se trouve à Leiden, coll. Huygens. Elle a été publiée par P.J. UylenbroekGa naar voetnoot1). Elle est la réponse au No. 2768. Chr. Huygens y répondit par le No. 2777. A Paris ce 23 Nov. 1692. J'ay receu avec bien du plaisir Monsieur la lettre que vous me faites l'honneur de m'ecrire du 23 octobre, je ne scais comment repondre à toutes vos honnestetez et je me trouve fort heureux que ma petite decouuerte merite vostre approbation. J'ay resolu pleinement tous les Problemes que vous me proposez, et comme vous me marquez auoir quelque enuie de voir le chemin, que j'ay tenu pour arriuer à ma construction, je vous enuoye vne methode tres simple et generale pour les cas semblables. Je l'ay trouuée en voulant mettre au net celle dont je m'etois serui qui est beaucoup plus embarassée. Pour reduire la somme des aady/y√aa+yy à la quadrature de l'hyperbole, j'oste les jncommensurables en suposant à la maniere de Diophante yz/a-a ∞ √aa+yy, ce qui donne y ∞ 2aaz/zz-aa et dy ∞-2aazzdz-2a⁴dz/qu. zz-aaGa naar einda), et mettant à la place de y et de dy leurs valeurs, l'on aura aady/y√aa+yy ∞ adn/nGa naar voetnoot2). C'est là tout le mistere, qui reussit dans vne jnfinité de cas qu'on auroit beaucoup de peine à reduire autrement. Jl est evident qu'il y a deux valeurs de z, l'vne vraye et l'autre fausse, dans l'egalité zzy-aay ∞ 2aaz. Je me suis serviGa naar eindb) des racines vrayes pour determiner la position de la courbe qui sert a rectifier la logarithmique, mais si l'on se seruoit des faussesGa naar voetnoot3), on trouueroit vne position de courbe qui me paroist plus propre pour la construction, la voicy:

[pagina 343]
Probleme.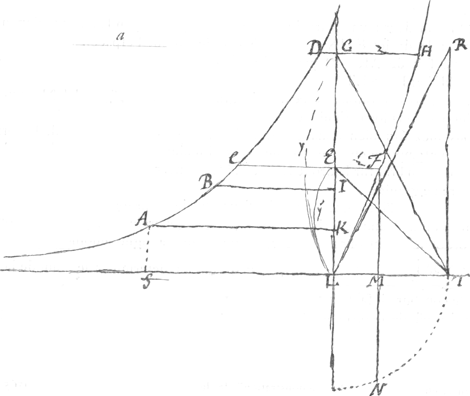 La logarithmique indefinie ABCD, qui a pour soutangente la droite donnée a, et son asymptote SL, etant données de position; trouuer geometriquement vne ligne droite egale à vne portion quelconque CD de cette courbe.
Solution. Soit menee par vn point quelconque L de l'asymptote SL la perpendiculaire LG, et soit decrite la courbe geometrique LFH, telle que (LE ou LG ∞ y, EF ou GH ∞ z) aay-zzy ∞ 2aaz, de sorte que l'on peut determiner par le cercle et la ligne droite la grandeur des ordonnées EF, GH, en supposant que les distances sur l'axe LE, LG soient données. Que l'on mene à present les paralleles CEF, DGH, à l'asymptote et ayant pris LT ∞ a, LK ∞ EF, LI ∞ GH, et mené les droites TG, TE, et les paralleles KA, IB, qui rencontrent la logarithmique aux points
[pagina 344]
A, B; je dis que la portion CD de la logarithmique ∞ TG-TE+AK-BIGa naar voetnoot4). 1^o. Si l'on mene TR parallele à LG, elle sera asymptote de la courbe geometrique LFH. 2^o. Si l'on prent TR double de LT la ligne LR sera tangente au sommet LGa naar voetnoot5). 3^o. Si l'on decrit vn quart de cercle qui ait pour rayon LT et que l'on mene librement la droite FMN parallele à LK, je dis que l'espace FLM est egal au rectangle fait de AK-BI par le double de LT; en supposant à present que LK ∞ MN et LI ∞ LTGa naar voetnoot6). 4^o. Je puis déterminer le centre de grauité de cette espace FLM en ne me seruant que de la logarithmiqueGa naar voetnoot7). Vous auez fort bien remarqué que l'on peut determiner le bras de la portion CD sur l'asymptote en se seruant de la logarithmique, mais il n'est pas aussi facile de trouuer son bras sur la droite LG ce qui seroit neanmoins necessaire pour auoir le centre de grauité. Je trouue aussi comme vous Monsieur que le demi-diametre du cercle qui mesure la plus grande courbure ∞ 3√¾ aa, et generalement que, si l'on nomme vne ordonnée quelconque AS, y, le rayon de la ligne euoluë au point A ∞ aa+yy√aa+yy/ayGa naar voetnoot8); d'où jl suit que, pour determiner le point de la plus grande courbure jl faut prendre y ∞ √½aaGa naar voetnoot9). Passons aux autres questions. La jre est de determiner la nature de la ligne courbe qui a pour soutangente
[pagina 345]
aax-2xxy/3aa-2xy. Je trouue trois courbes qui satisfont; la jre est l'hyperbole ordinaire xy ∞ aa et les deux autres sont yyx-aay ∓ x³ ∞ 0Ga naar voetnoot10): La seconde et troisieme sont de trouuer la ligne courbe, qui a pour soutangente 2x-yy/2x, auec la quadrature de l'espace curuiligne. La ligne est aayy-2aaxx ∓ 2y⁴ ∞ 0Ga naar voetnoot11), et l'espace curuiligne ∞ ⅔ xy-aax/6y, lorsque aayy+2y⁴ ∞ 2aaxxGa naar voetnoot12), mais lorsque aayy-2y⁴ ∞ 2aaxx, la courbe a vne position telle que l'on voit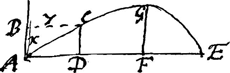 dans cette figureGa naar voetnoot13), ou AB ∞ x, BC ∞ y, AE ∞ √½aa et l'espace ECD ∞ (aa-2yy)√2aa-4yy/12a Si l'on prend AF ∞ ½a, FG sera la plus grande des ordonnées, et l'espace curuiligne EFG ∞ 1/24 aa. La 4^e et 5^e consistent à trouuer la ligne courbe qui a pour soutangente 2x+x³/yy et la quadrature de l'espace curuiligne. 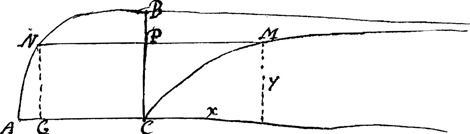Soit decrit le quart de cercle CAB et soit prolongée vne ordonnée quelconque
[pagina 346]
NP en M, de sorte que ∺ NP. CP. PM.Ga naar voetnoot14), le point M sera a la courbe requise. L'espace CPM est egal à l'espace circulaire AGNGa naar voetnoot15) le bras de l'espace CPM sur AC est double de celuy de l'espace AGN je puis aussi determiner le bras de l'espace CPM sur CB et partant le centre de grauité de cette espace. A l'egard des Problemes du Sieur Viuiani, jl y a pres de huit mois que Mr. l'Enuoyé de Florence me proposa celuy dont vous me parlez qui estoit sur vne feuille volante en forme d'enigme. Je luy en donnay aussi tost trois solutions auec la demonstration et j'en aurois pü trouuer par ma methode vne jnfinité d'autres mais cela ne vaut pas la peine que je vous en fasse jcy le detail. Le Sieur Viuiani m'a enuoyé depuis peu l'imprimé dont vous me parlez, qui ne renferme rien de considerable. Je n'ay point vû ce qui est dans les journaux de Leipsic de la figure d'une voile tendue par le vent car ces journaux ne viennent plus jcy depuis la guerre j'ay neanmoins donné ordre qu'on me fit venir ceux de cette année qui me manquent et quand je les auray receus je vous en mandray librement ma pensée puisque vous le souhaitez. Je vous prie de me faire sauoir s'il n'y a point de liures de mathematique nouueaux en angleterre, l'on m'a assuré que Mr. Neuton faisoit jmprimer pour la 2^e fois ses principes mathematiques d'une maniere qui estoit plus à la portée de tout le mondeGa naar voetnoot16), l'on m'a dit aussi de bonne part que Mr. Fatio auoit vn traitté de la pesanteur tout prest à jmprimerGa naar voetnoot17). Je voudrois bien sauoir aussi si Mr. Neuton fera jmprimer bientost ce qu'il a trouué sur la methode jnverse des tangentes et sur les quadratures je crois que Mr. GregoriGa naar voetnoot18) a donné depuis peu quelque chose sur ces matieres. Je suis, Monsieur auec vne estime tres particuliere Vostre treshumble et tres-obeissant serviteur Le Marquis de l'Hospital.
[pagina 347]
Je vous prie d'essayer si vos regles s'etendent à trouuer les lignes qui ont pour soutangentes √ay+xx et 2y³/yy+2yx-xx vous me ferez plaisir de me faire part de quelques Exemples où elles ne peuuent servirGa naar eindc). Holande A Monsieur Monsieur Christiaan Hugens Segneur de Zeelhem jn 't noordeinde naast de crabbe A la Haye.	voetnoot1) Chr. Hugenii etc. Exercitationes Mathematicae, Fasc. I, p. 240. einda) erat a³. qu. erat omissum [Christiaan Huygens]. voetnoot2) Lisez:-adz/z. eindb) C'est à dire dans les lignes precedentes [Christiaan Huygens]. voetnoot3) L'introduction des racines fausses revient, comme Huygens n'a pas manqué de le remarquer à la page 146 du livre H, à l'emploi de la substitution yz:a+a=√a²+y², qui mène aux relations a²y-z²y=2a²z et a²dy:y√a²+y²=adz:z. voetnoot4) On a, en effet, d'après la ‘demonstration’ de de l'Hospital (voir la Lettre N^o. 2765): arc CD=∫ydy/√a²+y²+∫a²dy/y√a²+y²=TG-TE+a∫dz/z; mais si z=EF ou GH, égal LK où LI, est considéré comme ordonnée de la logarithmique on a, si x en répresente l'abscisse, a dz/z=dx, donc a ∫dz/z=∫dx=AK-BI. voetnoot5) Propriétés qui se déduisent facilement à l'aide de l'équation y(a²-z²)=2a²z de la courbe LE. voetnoot6) Pour obtenir cette construction il suffit de remarquer qu'on a voetnoot7) La détermination de ce centre de gravité dépend en effet de celle des sommes z²dz:(a²-z²) et a²z²dz:(a²-z²)², qui se réduisent aux logarithmes. voetnoot8) Lisez: (aa+yy)√aa+yy/ay. voetnoot9) Tous ces résultats sont conformes à ceux obtenus par Huygens dans la pièce N^o. 2770. voetnoot10) On trouve pour la solution générale: xy²-a²y+Cx³=0. voetnoot11) Comparez la note 6 de la Lettre N^o. 2639. voetnoot12) Voir, pour la forme générale de cette courbe, la seconde figure (à la page 576) du § IV de la pièce N^o. 2644. La formule de de l'Hospital se rapporte probablement à l'espace curviligne compris entre l'axe des x, la courbe, et une ordonnée quelconque; mais alors on doit ajouter le terme: 1/6√2a²; peut-être ce terme lui a échappé parce qu'il croyait que l'expression a²x:6y s'annule pour x=0, y=0. voetnoot13) Comparez cette figure et les quadratures qui vont suivre avec celles de la courbe a²y²-2a²x²-y⁴=0 que l'on rencontre à la page 56 de la Lettre N^o. 2667 et qui se déduit de la courbe de notre texte en remplaçant a par a√2. voetnoot14) C'est-à-dire NP:CP=CP:PM, ou bien √a²-y²:y=y:x, d'où il suit x²(a²-y²)=y⁴; équation identique en effet avec celle de la Gutschovienne, indiquée par Huygens dans la Lettre N^o. 1065. voetnoot15) Ce résultat encore est identique avec celui de Huygens, annoncé dans la Lettre N^o. 1065. voetnoot16) Consultez, sur l'origine probable de cette nouvelle, la Lettre N^o. 2723. voetnoot17) Voir, sur ce projet de Fatio, la note 9 de la Lettre N^o. 2582 et les Lettres N^os. 2739 et 2745. voetnoot18) David Gregory, neveu de James, né à Aberdeen le 24 juin 1661, mort le 10 octobre 1710 à Maidenhead, Berkshire. Il fut professeur de mathématique à Edinburg et, depuis 1691, professeur d'astronomie à Oxford. eindc) En vient il des lignes geometriques [Christiaan Huygens].