Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 333]

N^o 2770.
Christiaan Huygens.
[octobre 1692].
Appendice II¹⁾ au No. 2768.

La pièce se trouve à Leiden, coll. Huygens.

Quaeritur punctum E, in logistica ubi maxima ejus curvitas; item radius EG et

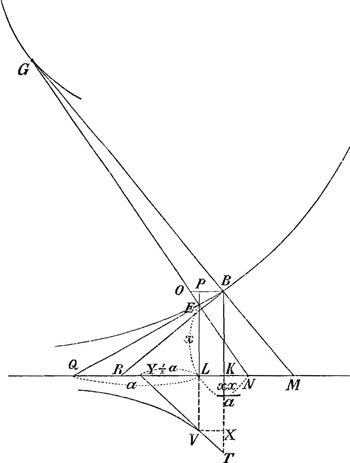
Fig. 1.

punctum G, unde descripta circuli circumferentia sit maxima earum quae logisticam in E intus contingant: fit EL=√½aa; LN=½a; EG=3EN.

EB logistica.

QM asymptotos ejus.

QE tangens EL perpendicularis ad asympt.

QL=a subtang.; EN perp. QE; RK=a; EL=x; BM perpend. RB.

LV=LN; KT=KM.

Erunt puncta V, T ad logisticam oppositam cujus eadem asymptotos QM, sed subtangens erit ½a; quia omnes LV, KT etc. proportionales sunt aeque ac EL, BK, etc.²⁾.

1) Calcul du rayon de courbure minimal de la logarithmique. Cet appendice est emprunté a la page 104 du livre H des Adversaria.

2) Probablement Huygens veut dire que puisque, d'après la définition même de la logarithmique (ou logistique), les ordonnées également distantes EL, BK, etc. de la courbe EB seront des proportionelles continues, il en devra être de même des LV, KT, etc. qui sont égales à EL²/a, BK²/a, etc., d'où il suit que la courbe VT sera encore une logarithmique. Comparez, à la page 176 du ‘Discours de la cause de la pesanteur’, les premières phrases de l'énumération des propriétés de la ligne logarithmique.

[p. 334]

Fig. 2.

Si autem BK=2EL [fig. 2] sit KT=4LV; unde si GH=2LV fit GL vel GK=½LK.

Et quia eadem ratio LV ad GH quae LE ad KB erit subtangens logisticae VT ad subtang. logisticae EB ut LG ad LK³⁾.

Ratio OB [fig. 1] ad BP:xx/a+a ad a^4).

ratio BP ad NM:½a ad ½a+xx/a; heac secundum methodum

nostrum in libro de Evolutione curvarum⁵⁾.

ratio OB ad NM sive EG ad GN:	½xx+½aa ad ½aa+xx
	xx+aa ad 2xx+aa

3) Consultez, à l'endroit cité du ‘Discours de la canse de la pesanteur’, la 5^e propriété, d'après laquelle la soustangente a est égale à la distance entre les ‘ordonnées de la raison double’, multipliée par un nombre constant.

4) Puisque OB/BP=QN/QL, et QL=a, QN=QL+EL²:QL=a+x²/a.

5) Allusion au passage suivant, que l'on rencontre dans la ‘Pars Tertia’: ‘De linearum curvarum evolutione et dimensione’ de l'‘Horologium Oscillatorium’ dans le texte de la ‘Propositio XI’: ‘At non aeque liquet quo pacto ratio [BP=] KL [voir la fig. 1 de cet appendice] ad MN innotescat, quam tamen semper quoque reperiri posse sic ostendemus’.
‘Sint rectae KT, LV, perpendiculares super KL, sitque KT aequalis KM, et LV aequalis LN, et ducatur VX parallela LN, quae occurrat ipsi KT in X. Quoniam ergo semper eadem est differentia duarum LK, NM quae duarum LN, KM, hoc est, quae duarum LV, KT; est autem differentiae ipsarum LV, KT aequalis XT, et XV ipsi LK; erit proinde NM aequalis duabus simul VX, XT....Atque adeo, si data fuerit ratio VX ad XT, data quoque erit ratio VX ad utramque simul VX, XT....hoc est, data erit ratio VX sive LK ad NM’.
‘Sciendum est autem, quoniam KT ipsi KM, et LV ipsi LN, aequales sumptae sunt, locum punctorum T, V fore lineam quandam vel rectam vel curvam datam....’
En appliquant ce passage au problème qui nous occupe, on trouve facilement: BP/NM==VX/VX+XT=YL/YL+LV, où LV=LN=xx/a et YL=½a, puisque la courbe VT est, comme on l'a vu, une logarithmique à soustangente ½ a.

[p. 335]