Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 336]

N^o 2771.
Christiaan Huygens.
27 octobre 1692.
Appendice III au No. 2768.

La pièce se trouve à Leiden, coll. Huygens.

Constructio J. Bernoulij ad Aenigma Viviani Florentia missi [sic] ad Leibnitzium cujus constructio alia ac non tam elegans sed tamen hujus fundamentum¹⁾.

Fig. 1.

GKB est quadrans semisphaerae. Polus G. Aequatoris quadrans BK. Centrum sphaerae A. BA, KA rectae. KHB est superficies ungulae dimidiae cylindricae 45 gr. super quadrante AKB.

A puncto quovis C in arcu BK sit CL parall. KH. CE perpend. BA. CL=CE. Arcus CF in quadrante CG aequalis sumatur arcui CB ac similiter alia puncta inveniantur in sphaerae superf.^m per quae transeat curva GFB²⁾. Dico spatium GFBCKG³⁾ aequari superficiei ungulae KBH. Ducatur enim radius CA et in eum perpend. FD, item CE perpend. in BA. Jam FD erit=CE vel CL. Quare spatiolum FC inter quadrantes minimo distantes qui à polo G ducuntur aequale fiet spatiolo CL eidem minimo arcui circumferentiae BC insistenti (hoc est notum theorema ex relatione superficiei sphaericae ad cylindricam circumscriptam)⁴⁾;

1) Voir, sur le problème de Viviani et les solutions de Jacques Bernoulli et de Leibniz, la note 17 de la Lettre N^o. 2768.

2) C'est la première construction de Jacques Bernoulli, communiquée sans démonstration dans l'article cité dans la note 17 de la Lettre N^o. 2768. En effet, BFG constitue le contour de l'une des quatre fenêtres perçant le dôme hémisphérique qui a pour base le grand cercle BG et pour sommet le point K.

3) Il est clair que l'aire GFBCKG constitue la quatrième partie de la surface restante du dôme.

4) C'est la méthode employée par Leibniz pour la quadrature de sa surface restante; cette surface diffère de celle de Bernoulli.

[p. 337]

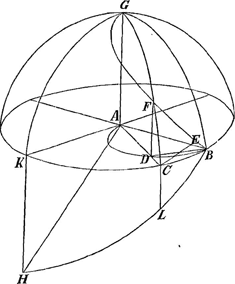
atque ita totum spatium superficiei sphaericae GFBCKG aequale superficiei semiungulae BCKH, ac proinde quadrato radii AB⁵⁾.

AC=AB; CD=EB quia FD=CE ex constructio; AD=AE; ergo triang. BAD ∞ CAE quia angulus communis ad A. Ergo cum ang. AEC sit rectus erit et ADB rectus. Ergo punctum D in semicircumferentia ADB. Ergo tota GFB super tota semicircumferentia ADB. Hinc GFB curva est in superficie semicylindrica super ADB⁶⁾. Hinc eadem est curva GFB atque in figura inferiore⁷⁾ AEFD. Nam sicut ibi⁸⁾ à B ad omnia puncta lineae AEFD sunt rectae aequales, ita hic à puncto A.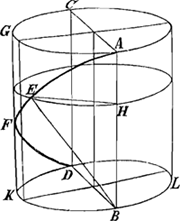

Fig. 2.

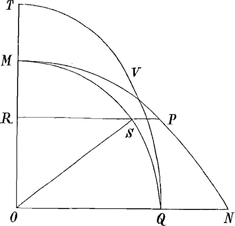Fig. 3.

Cylindri GL⁷⁾ latus AB aequale diametro ipsius BD. Radio BA centro B descripta est in cylindri superficie, linea curva AEFD. Si jam⁹⁾ in planum extendatur

5) On retrouve ce dernier théorème dans l'article de Leibniz, cité dans la note 17 de la Lettre N^o. 2768, où Leibniz (Acta, 1692, p. 277) ajoute: ‘Haec propositio etsi ex calculo nostro paulo ante posito statim derivari possit, quia tamen dudum innotuit Geometris, non est cur immoremur. Videantur qui de linea Sinuum et Cycloide egere’. En effet, en développant la surface cylindrique, la courbe BLH se transforme dans une sinusoïde, courbe dont la quadrature était bien-connue.

6) Ici finit la démonstration de l'identité de la solution de Jacques Bernoulli avec celle de Viviani exposée dans la Lettre N^o. 2768. Ce qui suit contient des recherches sur la courbe BFG.

7) Voir la figure 2 de cette pièce.

8) C'est-à-dire dans la courbe AEFD de la figure 2, dont la définition va suivre.

7) Voir la figure 2 de cette pièce.

9) Ce qui va suivre contient la démonstration d'une propriété remarquable de la courbe AEFD, qui consiste en ce que, si on l'enroule, avec la surface cylindrique qui la contient, sur un autre cylindre à rayon DB, touchant le cylindre donné le long de la droite AB, alors elle s'identifie avec l'intersection de ce nouveau cylindre avec un plan faisant un angle de 45^o avec sa base.

[p. 338]

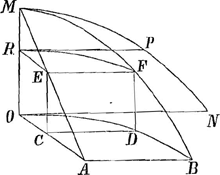
superficies hujus cylindri scissa secundum latus CD ipsi AB oppositum, erit spatium comprehensum curva AEFD, semicircumferentia DKB, et recta BA, eâdem figura et magnitudine atque MPNO [fig. 3] dimidium involucrum cylindricum ungulae anguli semirecti super semicirculo cujus radius OM aequalis AB sive AC¹⁰⁾.

Sumatur enim in curva AEFD punctum aliquod E, per quod ducatur planum basi cylindrici GL parallelum, faciens in cylindro circulum EH, cujus circumferentia secet AB in H, et jungantur HE, EB.

Accepiatur porro MR, pars radii MO, aequalis AH, et applicetur normaliter RP secans quadrantis MOQ arcum MQ in S, et jungatur SO.

Erit triang. ROS simile et aequale triang^o. HBE, quia RO=HB; OS=BE et anguli R et H recti. Ergo et RS=EH. Est autem circuli HE diameter subdupla diametri circuli MS. Ergo arcus EH aequalis arcui SM, hoc est rectae RP. Ergo explicatus arcus EH faciet applicatam ad AB, quam sit=RP, etc.

Si OT possit duplum OM¹¹⁾, et sit ellipsis quadrans OTVQ, erit curva TVQ=MPN. Ergo et ipsi AEFD¹²⁾.

10) On doit donc se représenter cette figure MPNO comme engendrée par le déroulement



de la courbe d'intersection MFB (voir la figure cicontre) d'un cylindre droit à base circulaire AODB (OA=OM) avec un plan passant par AB et faisant un angle de 45^o avec le plan du cercle ODB.
Il est clair, en effet, qu'alors, pour construire un point P de la courbe MPN on doit prendre RP égal à l'arc circulaire RF qui se confond avec l'arc MS de la figure 3 du texte, puisque RE=MR.

11) C'est-à-dire si OT²=2OM².

12) De cette manière la rectification de cette dernière courbe est réduite à celle d'un quadrant elliptique.