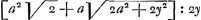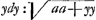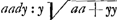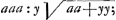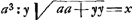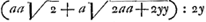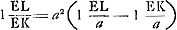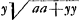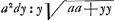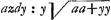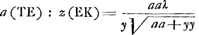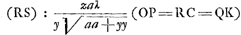Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 325]

N^o 2768.
Christiaan Huygens au Marquis de l'Hospital.
22 octobre 1692.

La minute se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek¹⁾.
La lettre est la réponse au No. 2765.
De l'Hospital y répondit par le No. 2775.

A Mr. le Marquis de l'Hospital.

22 Oct. 1692.

La reponse dont vous m'avez honorè, Monsieur, datée du 10 Sept., ne m'a estè rendue par Mr. Hartsoeker, que le 9 de ce mois, comme vous pouvez avoir appris de Mr. de la Hire²⁾. Il n'y avoit point de cachet, et je crois que ceux a qui vous en auiez bien voulu laisser voir le contenu, l'auront retenue si longtemps contre vostre intention. J'ay sujet de me plaindre d'avoir estè privè pendant pres d'un mois du plaisir de voir vostre excellente construction du probleme de la Logarithmique, qui m'a donnè de l'admiration et de l'exercice.

Je n'eus point de peine en faisant un peu de calcul de m'assurer de la veritè de vostre demonstration³⁾, mais de scavoir par quelle voie vous estes parvenu à cette solution, c'est ce que je n'ay pas encore tout à fait penetrè. La division de vos MN en deux parties est bien imaginée, dont la somme des unes ne m'a point retardè, parce que j'en avois rencontrè des semblables⁴⁾. Pour l'autre somme il me paroit

1) Chr. Hugenii Exercitationes Mathematicae, Fasc. I, p. 237.

2) Voir la Lettre N^o. 2767.

3) On rencontre cette vérification, qui ne présente rien de bien remarquable, à la page 99 du livre H des Adversaria. Disons seulement que Huygens y retrouve la valeur de OP ou KQ, indiquée par de l'Hospital, en appliquant la proportion:
PO:HP (ou dy)=GH (ou z): la soustangente de la courbe HI sur EL, et en calculant la valeur de cette soustangente, par la règle mentionnée dans la note 3 de la pièce N^o. 2612, à l'aide de la deuxième des formes de l'équation de la courbe HI, dans la note 6 de la Lettre N^o. 2765; tout en éliminant après coup le z au moyen de la première de ces formes.
De même il déduit ensuite la valeur de RS, donnée par de l'Hospital, à l'aide de la proportion:
RS:RC (ou QK)=a (la soustangente sur TE de la logarithmique): KE, où, d'après la construction de de l'Hospital, KE=GH=z=.

4) Des annotations de la page 99 du livre H, citée dans la note précédente, il résulte que Huygens n'a pas manqué de reconnaître que l'expression représentait l'accroissement de l'hypothénuse du triangle TFE, où TE=a, EF=y; d'où il suit immédiatement que la somme en question est égal à TG-TF.

[p. 326]

que vous l'avez reduite à la quadrature de l'hyperbole, en y reduisant la courbe dont l'équation est 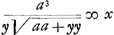, ce qui doit estre possible⁵⁾, mais il n'est pas aisè; et si vous avez quelque regle pour cela, ce que je seray fort aise de scavoir, je l'estime extremement. J'entrevois un autre chemin, par ou vous pourriez avoir passè, qui est de trouver qu'a la soutangente 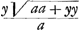convient vostre courbe geometrique aay+2aaz√2 ∞ 2yzz⁶⁾ mais ce chemin est plus

5) Voici comment cette remarque est motivée plus amplement à la page 107 du livre H: ‘Il a reduit la connoissance de la somme des dans la portion AB, à la quadrature de l'Hyperbole.
‘Comme les dy sont de petites lignes egales, si on met une ligne donnée, comme a au lieu de dy, on aura laquelle supposant =x, on aura une ligne courbe dans laquelle toutes les appliquées x seront à autant de a, comme la somme des à autant de dy dont la somme est connue. Et partant si on trouve la quadrature de cette courbe , ou bien a⁶=aaxxyy+y⁴xx, on aura la somme cherchée des . Ou elle sera reduite à la quadrature de l'hyperbole, et par consequent à la construction par la logarithmique, si la dite quadrature de la courbe se reduit à la quadrature de l'hyperbole. Ce qui assurement doit estre possible et cela est fort beau s'il a quelque regle pour cela. Car toutes les a, c'est à dire un rectangle donné, compris de FG et de la soutangente a, se trouvent icy estre à toutes les x, ou a l'espace de la courbe, comme la ligne LD-KC à GF [lisez: comme GF à LD-KC], c'est à dire comme le dit ▭ FG, a à un espace hyperbolique sur l'asymptote (c'est à dire dans l'hyperbole equilatère dont le quarré à l'angle des asymptotes est aa) duquel espace les perpendiculaires soient en raison des deux , estant y=EG; car cet espace hyperbolique est au quarré de l'angle comme LD-KC à la soutangente a; donques toutes les dites x, ou l'espace de la courbe est égal à cet espace hyperbolique’. (Remarquons qu'en effet, puisque d'après l'énoncé du problème dans la Lettre N^o. 2765, les deux valeurs représentent les lignes FI (=EL) et GH (=EK), l'espace hyperbolique mentionné égale a². , ou bien, en conséquence de la propriété principale de la ligne logarithmique: a(LD-KC).
Ensuite Huygens ajoute encore: ‘Il est plus vraisemblable qu'il ait tenu ce chemin, que celui qui est marqué à la sin de la page 101 [voir la note qui suit]. Car il est malaisé de s'en aviser, et il faudroit avec cela connoitre que :a est soutangente à la ligne géométrique 2zzy=aay+2aaz√2, qui est HOI, ce que je tiens très difficile. Il peut avoir employé cette HOI, trouvée par la precedente reduction pour servir à sa demonstration’.

6) En supposant inconnue l'équation de la courbe HOI, mais en admettant en principe la construction de de l'Hospital, d'après laquelle RS devait représenter , d'où il suivit, par la propriété de la logarithmique, RC (=QK=PO)= pour y=EG, z=EK=GH, il était en effet facile de calculer la valeur de la soustangente sur EL de cette courbe HOI, après quoi il s'agissait de remonter par là à son équstion.
C'est ce raisonnement que l'on reconnaître dans les phrases qui suivent et que nous avons empruntées à la page 101 du livre H:

GH=z incerta adhuc, sed quaecunque futura est, eam statui ponere in EK ad Logarithmicam, ut et PO in RC, et habere SR pro aaλ:. Quaeretur quanta tunc futura sit RC vel OP, et fit zaλ:; unde tunc curva HOI quaeritur ex subtangente sua :a. Et invenitur esse geometrica. Unde cognoscitur ratio duarum GH FI; seu EK, EL.’
Inutile d'ajouter qu'au point de vue moderne le problème n'en était guère avancé, puis qu'il se réduisait de cette manière à l'intégration de l'équation différentielle azdy= dz qui dépend de l'intégrale même qu'il s'agit de trouver.

[p. 327]

detournè, et la difficultè n'est pas petite de trouver la courbe pour cette soutangente donnée. J'avoue que je n'ay gueres approfondi ces matieres, m'estant exercè principalement à appliquer la geometrie à d'autres speculations ou elle peut avoir quelque usage. Je scay bien que ces quadratures des courbes et le probleme renversè des Tangentes en bien des occasions peuvent estre de fort grande utilitè, mais voiant le progres que Mess.^rs Leibnitz, Fatio et Newton y avoient faits, devant que j'y eusse songè, j'ay taschè plustost de profiter de leur travail que de me mettre à chercher apres eux, sur tout depuis que Mr. Fatio m'a fait esperer⁷⁾ la publication d'un traitè de Mr. Newton sur ce sujet, qui, à son avis, en scait bien plus que luy et Mr. Leibnitz ensemble.

J'ay remarquè en examinant vostre invention, qu'on peut aussi trouver la surface du solide mesme infini⁸⁾, que fait une portion de la Logarithmique en tournant sur la soustangente, c'est-à-dire luy trouver un cercle egal, en se servant comme vous, Monsieur, de la ligné mesme, d'où s'ensuivent les centres de gravitè des portions lineaires⁹⁾. J'ay aussi determinè le cercle qui mesure sa plus grande courbure¹⁰⁾; mais tout cela est aisè et nullement comparable à ce que vous avez fait. Vous scavez fort bien l'usage à ce que je vois, des dx et dy de Mr.

7) Comparez la Lettre N^o. 2745.

8) Voir l'Appendice I de cette lettre, la pièce N^o. 2769.

9) A l'aide de la règle de Guldin, puisque la longueur de la courbe peut se construire par le théorème de de l'Hospital.

10) Voir l'Appendice II à cette lettre, la pièce N^o. 2770.

[p. 328]

Leibnitz, qui assurement a quelque chose de fort bon, en ce qu'il nous fait appercevoir souvent des veritez et des consequences, qui ne se presenteroient pas sans cela.

Je mets icy, puis que vous l'avez souhaité, 3 questions, que je luy ay cy-devant proposées¹¹⁾.

L'une estoit, de trouver la ligne courbe AB par sa soutangente donnée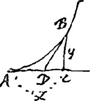



CD ∞ aax-2xxy/3aa-2xy; AC estant x et l'appliquée CB y.

La 2^e. estoit de trouver la courbe quand la soutangente est 2x-yy/2x.

La 3^e. de trouver la quadrature de cette mesme courbe. J'adjoute encore celle cy: de trouver la courbe et sa quadrature, ou a quoy elle se reduit, quand la soustangente est 2x+x³/yy¹²⁾.

J'ay des regles pour ces problemes horsmis les quadratures¹³⁾. Et mesme ces regles ne resolvent pas tous les cas, encore qu'il n'y ait point de racines meslées. Et pour ceux ou il y a racine, la regle que j'ay de Mr. Leibnitz¹⁴⁾ ne sert que peu souvent et nullement en la soutangente de cy-dessus y√aa+yy/a. Il a resolu les 3 questions que je viens de raporter horsmis la premiere par ce qu'il arriva par accident que je lui decouvris la courbe dont il s'agissoit¹⁵⁾. Ayant desia estè

11) Voir, pour les deux premiers problèmes la Lettre N^o. 2611, les notes 3 et 5 de la Lettre N^o. 2612 et la Lettre N^o. 2643; pour le troisième, où il s'agit de la quadrature des courbes 2a²x²=a²y² ± y⁴, on pent consulter la Lettre N^o. 2667, aux pages 56 et 57.

12) Voir, sur ce problème, la note 15 de la Lettre N^o. 2735.

13) Il s'agit de la méthode de Fatio; consultez la note 11 de la Lettre N^o. 2465.

14) Voir la pièce N^o. 2713.

15) En effet, par suite du malentendu sur le signe de la soustangente, dont il est question dans la note 3 de la Lettre N^o. 2612, Leibniz avait cherché et trouvé (voir la Lettre N^o. 2627) la solution de l'équation différentielle ydx/dy=(2x²y-a²x):(3a²-2xy), tandis que le problème, tel que Huygens l'avait entendu, devait mener à une équation qui diffère par le signe du second membre. Alors Huygens, pour convaincre Leibniz de la fausseté prétendue de sa solution, lui avait révélé, dans sa Lettre N^o. 2633, l'équation de la courbe à laquelle convenait la soustangente donnée. Leibniz d'ailleurs avoua dans sa Lettre N^o. 2636 que, pour résoudre le problème tel que Huygens l'avait conçu, il aurait dû ‘avoir recours à d'autres adresses’ dont il ne s'était pas servi parce qu'il avait trouvé fort aisément ce qui lui avait été demandé.

[p. 329]

trop long, je ne vous proposeray rien de physico-mathematique, et je ne scay mesme si je trouverois maintenant rien en ce genre qui meritast vostre meditation.

Je viens de recevoir un imprimè de Florence du Sigr. Viviani, avec le titre extravagant de Formatione e misura de tutti i cieli¹⁶⁾. Il contient la solution de quelques Problemes Geometriques, mais sans demonstration, des quels le principal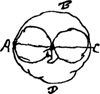



est la quadrature du reste d'une surface spherique, quand on en oste ce qu'emportent deux forets cylindriques qui la percent tout outre. La sphere est ABCD, les forets ou leurs trous cylindriques AE, EC, occupant chacun la moitiè du diametre de la sphere¹⁷⁾. Les problemes de Geometrie pure sont infinis, des quels j'estime le moins ceux où l'on se forge tout expres des lignes ou des surfaces, auparavant inconnues ni vues dans la nature, pour en rechercher les proprietez, comme je vois que font souvent quelques Geometres Allemans, entre autres celuy qui, dans un des derniers journaux de Leipsich, a entrepris de determiner la figure du voile tendu par le vent, ou je crois qu'il s'est trompè par quelque faux principe¹⁸⁾. Je seray bien aise, Monsieur, d'en apprendre vostre sentiment, estant persuadè plus que jamais de l'excellence de vostre scavoir et jugement en ces matieres. Je suis avec respect, etc.

Pardonnez a mon impatience si je vous supplie tres humblement de me faire tenir sans de si longs detours celles que vous me ferez l'honneur de m'escrire, et

16) ‘Formazione e misura di tutti i cieli, con la struttura e quadratura esatte del' intero, e delle parti d'un nuovo cielo ammirabile, e di uno degli antichi delle volte regolari degli architetti’. Firenze 1692. in-4^o.

17) Il s'agit de la solution, donnée par Viviani lui-même, d'un problème qu'il avait posé aux géomètres, sous le pseudonyme: D. Pius Lisci pusillus Geometra, anagramme de: postremus Galilei discipulus, dans une feuille volante, datée du 4 avril 1692 et qui portait le titre: ‘Aenigma geometricum de miro opificio Testitudinis Quadrabilis Hemisphaericae’.
Le problème revenait à celui de percer un dôme hémisphérique par quatre fenètres égales de sorte que le restant de la surface était absolument quadrable.
Il fut résolu de plusieurs manières différentes entre autres par Leibniz, dans les ‘Acta’ de juin 1692, et par Jacques Bernoulli, dans ceux d'août 1692, sous les titres: ‘Constructio testudinis quadrabilis hemisphaericae; Autore G.G.L.’ et ‘Aenigmatis Florentini solutiones varie infinitae, per I.B.’
A la page 115 du livre H des Adversaria on rencontre, sous la date: ‘Hofwici 27 Oct. 1692’, une discussion de la première solution de Bernoulli et la démonstration de son identité avec celle de Viviani, rapportée dans le texte de cette lettre. Nous les reproduisons dans la pièce N^o. 2771, comme Appendice III à la présente lettre.

18) Voir la note 33 de la Lettre N^o. 2693

[p. 330]

faites adjouter s'il vous plait à la superscription après mon nom, Seignr. de Zeelhem, ce qui me distingue de mon frere aisnè.