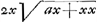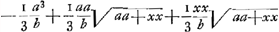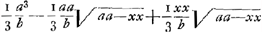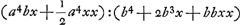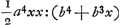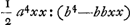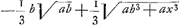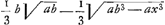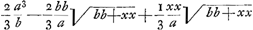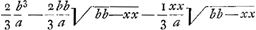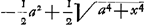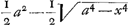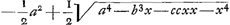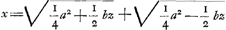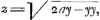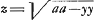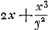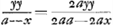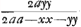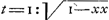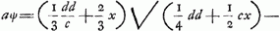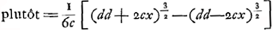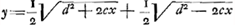Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–
[pagina 244]
| |
No 2735.
| |
[pagina 245]
| |
examinavi et recte se habere comperi, unde et de caeteris nihil ambigo. An autem eadem methodo hic utaris, qua egoGa naar voetnoot3) (quae nempe ex Barovij TheoremateGa naar voetnoot4) quodam pendet) ignoro. Sed insigni industria saepe usum te adverto in ejusmodi quadraturis formandis, unde aequationes curvarum oriantur, quae paucis terminis constent; nisi forsan aliunde, ut fit, quadraturas istas eruerasGa naar voetnoot5). Nam contraria via ex aequatione ad quadraturam pergere, etsi nonnumquam contingat, vix id in tuis illis concedi crediderim, nec Tschirnhausio se hic jactanti fidemGa naar voetnoot6) habeo. Evenit quidem mihi, ut cum aequationem curvae 15ti.Ga naar voetnoot7) exempli tui celebri geometrae proposuissemGa naar voetnoot8), ille quadraturam ejus, qualis tua est, invenerit, cum et ego meam | |
[pagina 246]
| |
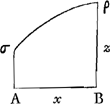
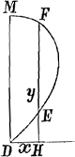
haberemGa naar voetnoot9), sed suspicor a posteriori, ex collectis tuo modo exemplis, id eum praestitisse. Quamquam autem innumeras curvas quadrabiles ita invenire liceat, non inde sequitur talem quadraturam effici posse, cui curva quaedam, quam tibi quadrandam proponis, conveniat. Ac proinde non video, quo pacto pag. 9Ga naar voetnoot10), ex solutione problematis tui a posteriori, concludas omnium curvarum quadraturas haberi posse. Nam ex. gr. cum aequatio circuli sit 2ay-yy ∞ xx, an putas quadraturam talem aliquam excogitari posse pag. 6.a vel 8.a ut inde haec aequatio nascatur. Hoc ex tuis nequaquam efficitur, et frustra te fatigares. Recte autem affirmas totum quadraturae negotium hinc pendere, ut ex data linea tua BC (quam brevitatis gratia subnormalem vocare soleo, quia normali in curvam ductae subjacet) inveniatur aequatio curvae, ad quam pertinet. Si enim subnormalis haec
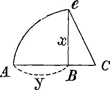 BC detur 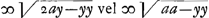 , possisque hinc curvam propriam invenire, jam constat te quadraturam circuli habiturumGa naar voetnoot11), utque proinde pag. 12, ad septimam potestatem literae y adscenderent nil opus fuerit. Caeterum hoc problema eximium jam diu geometras peritissimos exercet, nec putandum est, ipsum semper solutionem admittere. Vellem tantum hoc definiri posset, an subnormalis data ad curvam geometricam pertineat an ad alîus generis aliquam, an denique ad nullam. Habemus quidem rem confectamGa naar voetnoot12) finitis casibus, ubi subnormales dantur absque radicalibus quantitatibus, ut si sit subnormalisGa naar voetnoot13) , possisque hinc curvam propriam invenire, jam constat te quadraturam circuli habiturumGa naar voetnoot11), utque proinde pag. 12, ad septimam potestatem literae y adscenderent nil opus fuerit. Caeterum hoc problema eximium jam diu geometras peritissimos exercet, nec putandum est, ipsum semper solutionem admittere. Vellem tantum hoc definiri posset, an subnormalis data ad curvam geometricam pertineat an ad alîus generis aliquam, an denique ad nullam. Habemus quidem rem confectamGa naar voetnoot12) finitis casibus, ubi subnormales dantur absque radicalibus quantitatibus, ut si sit subnormalisGa naar voetnoot13) 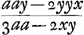 Ga naar voetnoot14) vel Ga naar voetnoot14) vel 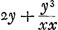 Ga naar voetnoot15), repe- Ga naar voetnoot15), repe- | |
[pagina 247]
| |
rientur aequationes curvarum geometricarum, quibus hae conveniunt. Aliis vero casibus non succedet; ut, si detur subnormalis 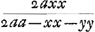 Ga naar voetnoot16), hic cessat regula. Rursus alijs casibus alia methodo ad quadraturas res deducitur, ut si detur subnormalis xx/aGa naar voetnoot17), vel Ga naar voetnoot16), hic cessat regula. Rursus alijs casibus alia methodo ad quadraturas res deducitur, ut si detur subnormalis xx/aGa naar voetnoot17), vel 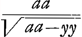 Ga naar voetnoot18), invenitur, ad prioris curvae quaesitae puncta designanda, hyperbolae quadraturam requiri; ad posterioris, tum circuli tum hyperbolae. Horum aliquid an tibi compertum sit scire velim. Item quo modo pag. 10. solutionem secundae propositionis tuae, cum quadratura per x datur, ad qua- Ga naar voetnoot18), invenitur, ad prioris curvae quaesitae puncta designanda, hyperbolae quadraturam requiri; ad posterioris, tum circuli tum hyperbolae. Horum aliquid an tibi compertum sit scire velim. Item quo modo pag. 10. solutionem secundae propositionis tuae, cum quadratura per x datur, ad qua- | |
[pagina 248]
| |
draturas Hyperbolae aut circuli deducas, et an semper eo devenias, etiamsi curva quaesita sit geometrica? Velut cum datur quadratura ista: aψ∞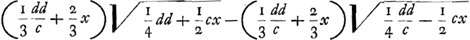 Ga naar voetnoot19), ubi curvae aequatio est y4 ∞ ddyy-ccxx, eadem quae in tuo 15o. casuGa naar voetnoot20). Non intelligo etiam quali calculo ex quadraturis pag. 8 elicies aequationes curvarum pag. 9. Ad haec omnia ut mihi rescribas etiam atque etiam a Te peto. Tum ut de te ipso docere velis, qui sis, et ex qua Huygheniorum familia, nam non esse eandem, nostra armorum insignia ostendunt. Vale! Ga naar voetnoot19), ubi curvae aequatio est y4 ∞ ddyy-ccxx, eadem quae in tuo 15o. casuGa naar voetnoot20). Non intelligo etiam quali calculo ex quadraturis pag. 8 elicies aequationes curvarum pag. 9. Ad haec omnia ut mihi rescribas etiam atque etiam a Te peto. Tum ut de te ipso docere velis, qui sis, et ex qua Huygheniorum familia, nam non esse eandem, nostra armorum insignia ostendunt. Vale!
Dabam Hagae Com. 12 Feb. 1692. |
|