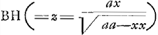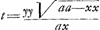Oeuvres complètes. Tome X. Correspondance 1691-1695

(1905)–Christiaan Huygens– rechtenstatus



[pagina 209]
N^o 2721. Christiaan Huygens à N. Fatio de Duillier. 18 décembre 1691. La lettre se trouve à Genève, Bibliothèque Publique. Le sommaire se trouve à Leiden, coll. Huygens. La lettre fait suite au No. 2700. Fatio de Duillier y répondit par le No. 2723. Sommaire: 18 Dec. a Mr. Fatio, que j'ay respondu a sa lettre et envoiè les Errata de NewtonGa naar voetnoot1). que M. Leibnits m'a envoiè de sa methode &c. qu'il aille prendre de mon frere l'Exemplaire de mon livre de la lum.re pour le donner a Mr. Bernard. Baisemains aux amis et a Mr. Locke un compliment. que j'ay donnè quelque chose en matière de musique a Mr. de BeauvalGa naar voetnoot2). Fatio loge chez M. Tourton et compag.^e A la Haye ce 18 Dec. 1691. Monsieur Depuis que vous estes en Angleterre je n'ay receu de vos lettres que celle du 8/18 Sept.Ga naar voetnoot3) à laquelle je respondis aussi tost, et vous envoyay les Errata de Mons.r Newton, apres en avoir pris copie. Je crois vous avoir escrit alors qu'il est à souhaiter que cet Illustre autheur fist faire une seconde Edition de son Livre, où tous ces Errata pourroient estre corrigez, et beaucoup de choses obscures eclaircies, et je vous recommande derechef de l'en vouloir soliciter, en luy faisant s'il vous plait mes tres humbles baise-mains. J'ay a la fin receu de Mr. Leibnitz quelque parcelle de sa methodeGa naar voetnoot4) pour le Probleme renversè des Tangentes. La Preface, qui est magnifique, à sa mode, contient 2 pages, et l'instruction une et demie seulement, mais il y a dans celle-cy, tant d'obscuritè que je n'en scaurois venir à boutGa naar voetnoot5), de sorte que je l'ay priè de me l'expliquer plus clairement devant que je luy envoie vostre methode. Et comme vous estes encore moins versè que moy dans son calculus differentialis j'ay cru qu'il ne serviroit de rien de vous faire part de ce qu'il m'a envoiè, jusques a ce que j'aye cet eclaircissement. Habeo (dit il) diversas vias quibus magnum hoc problema in oblatis casibus aggrediar, sed hanc optimam esse judico (quoties ea uti licet) ut Problema Tangentium inversum revocetur ad
[pagina 210]
quadraturas. Car quoy qu'il ait une autre methode plus absolue, quaeque non indiget alijs praecognitis, il arrive pourtant souvent que le calcul y monte trop haut, et pour cela il s'arreste à celle qui est par les quadratures comme estant plus commode. Or ce que je trouve a dire à cecy, comme je luy ay aussi remontrè, c'est que quand on a reduit le probleme a quelque quadrature inconnue, on n'a rien avancè si on ne scait comment trouver cette quadrature, ou comment demontrer son impossibilitè. Et je ne scay, si parfois on ne parviendroit pas à des quadratures impossibles, quoy que le problème de la tangente fust possible. Voicy l'une de ses Propositions, Quandocunque proprietas tangentium data exhibet valorem Subtangentialis per solam (ex indeterminatis) abscissam, vel per solam ordinatam, problema reducitur ad quadraturas. En quoy les racines sont aussi comprises. L'autre proposition est. Si valor subtangentialis detur per x et y simul, tunc non semper facile est reducere problema ad quadraturas, infiniti tamen sunt casus ubi res procedit, et generaliter hoc pronuntiari potest, Quandocunque valor subtangentialis est productum ex duabus quantitatibus seu formulis, quarum una datur per solam abscissam x; altera per solam ordinatam y, tunc problema reducitur ad quadraturas. Il y a quelque chose de bon icy en ce que les racines ne sont pas exceptées, mais vous voiez d'ailleurs quelle infinitè de cas se peuvent resoudre par vostre methode, qui ne tombent pas sous celles-cy, outre ceux qui se resolvent absolument par la vostre, et qui par celle de Mr. Leibnitz aboutiroient à quelque quadrature peut estre inconnüe. Il met pour exemple de cette seconde Proposition, de chercher la courbe dont je luy avois cy devant donnè la soustangenteGa naar voetnoot6)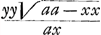 . Il reduit ce problème à la quadrature de la courbe AH. c'est à dire a celle de son espace indefiniment pris, AHB; cette courbe s'exprimant par cette Equation 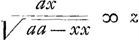, ou aaxx-aazz+xxzz ∞ o, Et il donne ensuite cette quadrature, et par elle il trouve que la courbe cherchée, qui a sa soutangente 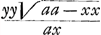, s'exprime par cette Equation, y⁴ ∞ 4aayy-4aaxx. Or je sçavais fort bien cette quadrature de la courbe AH, qui est celle que je vous proposayGa naar voetnoot7) pour trouver par elle
[pagina 211]
l'Equation de la courbe; et je scavois aussi que cette quadrature estant donnée, mon probleme estoit résoluGa naar voetnoot8); mais je crus en le luy proposant qu'il le resoudroit 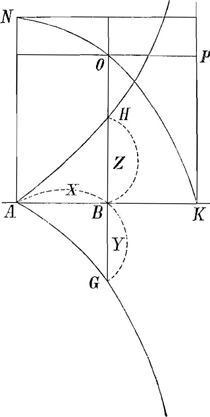independamment, et qu'ainsi sa methode des tangentes renversée produirait la quadrature de la ligne AH. Mais cela a estè autrement, et il a falu qu'il cherchast cette quadrature. Je ne scay pas par quel moien, mais c'est ce qu'il devroit m'apprendre, pour me rendre sa methode de quelque usage. Vous connaissez cette courbe AHGa naar voetnoot7) dont l'espace AHB ∞=NP, quand NOK est un quart de inconference. J'ay donnè a mon frère de Zulichem un Exemplaire de mon traitè de la LumiereGa naar voetnoot9), que je vous prie Monsieur de luy demander, et de le faire tenir à Mons.r Bernard, dont le nom y est escrit à la premiere page. Je l'avois oubliè malheureusement lors que j'en fis la distributionGa naar voetnoot10) et il ne s'est guere falu que je n'aie encore une fois oubliè d'avoir chargè mon frere de cet Exemplaire. Si vous avez occasion de voir Mons.r BernardGa naar voetnoot11) vous luy direz, s'il vous plaist, que je suis bien honteux de m'acquitter si tard de cette dette, ou bien vous le luy ferez sçavoir
[pagina 212]
par d'autres. Vous m'obligerez aussi si vous voulez bien assurer de mes respects nos Illustres amis Monsieur Boyle, Monsieur Hamden, Monsieur Locke que je suis faschè de n'avoir pas assez connu quand j'estois en AngleterreGa naar voetnoot12), et a qui je suis obligè non uno nomineGa naar voetnoot13). Je seray fort aise d'apprendre que vous vous portiez bien et que vous vous souveniez Monsieur de Vostre treshumble et tresobeissant serviteur Hugens de Zulichem. J'ay donnè quelque chose en matière de Musique a Mr. de Beauval que vous pourrez voir dan son JournalGa naar voetnoot14).	voetnoot1) Voir la pièce N^o. 2698. voetnoot2) Voir la pièce N^o. 2705. voetnoot3) Notre N^o. 2697. voetnoot4) Voir la pièce N^o. 2713. voetnoot5) Huygens y a réussi le jour suivant; voir la note 5 de la Lettre N^o. 2726. En conséquence, Huygens a modifié, dans sa lettre à Leibniz, N^o. 2726, le passage où il motive le délai de l'envoi de la méthode de Fatio. voetnoot6) Voir la Lettre N^o. 2660. voetnoot7) Voir la Lettre N^o. 2672. La courbe AON de cette lettre est, en effet, identique avec la courbe AH. voetnoot8) Comment Huygens le savait, c'est ce qui résulte de quelques annotations qui se trouvent à la page 84 recto du livre G des Adversaria, savoir, à l'aide d'un théorème de Barrow, publié et démontré dans la Lectio Geometrica XI (p. 85 de l'édition de 1674) de ses Lectiones Opticae & Geometricae, citées dans la Lettre N^o. 1767, note 14. En effet, d'après ce théorème, on a:½ BG²=spat. AHB, pourvu que représente la sousnormale de la courbe AG. Or, à une sousnormale de cette valeur correspond la soustangente ; il est donc clair que la détermination de l'équation de la courbe AG, désinie par cette soustangente, dépendait de la quadrature de la courbe ABH. voetnoot7) Voir la Lettre N^o. 2672. La courbe AON de cette lettre est, en effet, identique avec la courbe AH. voetnoot9) Constantyn Huygens était parti en Octobre 1691 pour suivre le Roi en Angleterre. voetnoot10) Voir la Lettre N^o. 2569, note 1. voetnoot11) Sur Edward Bernard; voir la Lettre N^o. 1885, note 10. voetnoot12) En 1689. Consultez la Lettre N^o. 2544, note 1. voetnoot13) Comparez le dernier alinéa de la Lettre N^o. 2572. voetnoot14) Voir la pièce N^o. 2705.