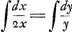Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–No 2726.
| |
[pagina 222]
| |
ponse, mais songeant que vous attendez peut-estre ce que j'auray à dire touchant vostre EscritGa naar voetnoot4), qu'il m'a envoiè, je ne veux pas laisser une plus longue interruption à nostre correspondance dont je tire du plaisir et de l'avantage. Vous scaurez donc touchant cet Escrit que j'ay eu de la peine d'abord à l'entendre, estant encore peu accoutumé à vostre maniere de calcul et ne demeslant pas assez bien les constructions qui resultent de vos solutions. Pourtant y estant retournèGa naar voetnoot5) avec plus de loisir j'en suis venu à boutGa naar voetnoot6). Mais qu'ay je trouvè? J'ay vu qu'en reduisant le Probleme renversè des Tangentes aux quadratures, vostre methode ne me donnoit pas ce que j'en esperois d'avantage, qui estoit de m'en pouvoir servir pour trouver les quadratures. Je scavois fort bien celle de la Courbe que vous expliquez et demonstrez, et comment par là on pouvoit construire la courbe dont la soutangente est yy 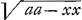 :axGa naar voetnoot7), mais je croiois que par vostre methode ontrouveroit cette courbe independamment, et par elle la quadrature de l'autre, ce qui
n'est point. J'ay vu de plus, en essaiant vostre methode sur plusieurs courbes connuesGa naar voetnoot8), feignant qu'elles ne le fussent point, mais seulement les proprietez de leurs tangentes, que tousjours j'estois reduit à des quadratures impossibles, comme de :axGa naar voetnoot7), mais je croiois que par vostre methode ontrouveroit cette courbe independamment, et par elle la quadrature de l'autre, ce qui
n'est point. J'ay vu de plus, en essaiant vostre methode sur plusieurs courbes connuesGa naar voetnoot8), feignant qu'elles ne le fussent point, mais seulement les proprietez de leurs tangentes, que tousjours j'estois reduit à des quadratures impossibles, comme de
| |
[pagina 223]
| |
l'Hyperbole, du Cercle et autres, au lieu que par la methode de Mr. Fatio l'on trouve l'equation de la ligne cherchée sans aucune necessité d'en quadrer d'autres. Vous n'enseignez donc pas à discerner si la ligne cherchée est geometrique ou non, et s'il faut ces quadratures de l'Hyperbole et autres pour la construire. Par exemple, si la soutangente est 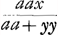 Ga naar voetnoot9), la construction de la courbe cherchée se reduit par vostre methode à la quadrature de l'Hyperbole et à celle de la courbe Ga naar voetnoot9), la construction de la courbe cherchée se reduit par vostre methode à la quadrature de l'Hyperbole et à celle de la courbe 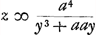 Ga naar voetnoot10). Et de mesme si la soutangente est Ga naar voetnoot10). Et de mesme si la soutangente est 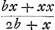 Ga naar voetnoot11), vous viendrez derechef à la quadrature de l'Hyperbole et à celle d'une autre courbe, au lieu que Mr. Fatio n'a besoin d'aucune. On ne tient donc rien par vostre methode, si on ne scait trouver les quadratures quand elles sont possibles, et Ga naar voetnoot11), vous viendrez derechef à la quadrature de l'Hyperbole et à celle d'une autre courbe, au lieu que Mr. Fatio n'a besoin d'aucune. On ne tient donc rien par vostre methode, si on ne scait trouver les quadratures quand elles sont possibles, et
| |
[pagina 224]
| |
connoitre quand elles sont impossibles, en quoy je scay par experience que vous avez quelque chose de beau, et cela paroit, dans l'exemple que vous avez mis à la fin, où vous quadrez la courbe aaxx+xxyy-aayy ∞ 0. Je l'avois aussi trouvée, comme j'ay dit, mais c'avoit estè par rencontre, et mesme par cette quadrature que je donnay à Mr. Fatio, il trouva l'equation de la courbe à qui elle convenoitGa naar voetnoot12). Considerant tout ce que je viens de dire, et voiant de plus, Monsieur, que vous appellez cette methode qui reduit aux quadratures la meilleure des vostres pour ce probleme, il m'est aisè de conclure que vous ne m'en avez envoiè qu'une petite partie, vous reservant d'y joindre par apres le reste, et qui fait presque le tout. Si je pouvois en faire de mesme en ce qui est de la methode de Mr. Fatio, je vous imiterois, mais elle est telle que vous decouvrant une partie, ce seroit vous apprendre tout. Resolvez vous donc je vous prie à m'envoier cette principale partie, a fin que Mr. Fatio ne puisse pasGa naar voetnoot13) me reprocher d'avoir trocqué χρόσεα χάλϰείων, car vous voiez bien apres tout que je ne suis pas seul maitre de la chose. En estudiant les exemples que vous donnez de vostre reduction, je me suis rendu vostre maniere de calcul un peu plus familiere qu'elle ne m'estoit, et je la trouve excellente pour representer avec facilitè et clartè ces summas minimorum, qui servent en beaucoup d'occasions. Mais je ne vois pas encore en considerant vostre equation de la Cycloide, de quel secours elle seroit pour en deduire omnia circa Cycloidem inventa, comme vous dites. Car quand ce ne seroit que pour trouver l'espace compris de cette ligne et sa base, ne faudroit il pas emploier à peu pres les mesmes biais dont on s'est servi pour cette dimension. Et s'il faloit trouver le centre de gravitè de la demie Cycloide, vostre calcul vous y meneroit il sans ces profondes speculations de Mr. PascalGa naar voetnoot14) ou WallisGa naar voetnoot15)? Vos expressions pourroient estre plus courtes, mais pour l'invention je crois qu'il faudroit passer à peu pres par les mesmes chemins. Si cela est autrement, vous me ferez plaisir de me detromper, afin que j'aye toute la bonne opinion de vostre calculus differentialis qu'il merite. Si vous lisez l'Histoire des ouvrages des Scavants qu'on publie icy de 3 en 3 mois, vous y trouverez quelque chose de moy en matiere de MusiqueGa naar voetnoot16) et qui regarde | |
[pagina 225]
| |
un nouveau systeme des Tons. Si Mrs. de Leipsich avoient envie de le mettre dans leurs ActaGa naar voetnoot17), j'y pourray joindre quelques autres nouvelles considerations. Je vous souhaite la nouvelle année heureuse et suis etc. |
|