Oeuvres complètes. Tome II. Correspondance 1657-1659

N^o 494.
Problèmes de Bl. Pascal.
juin 1658.
Appendice au No. 493.

La pièce a été publiée dans les Oeuvres Complètes de Bl. Pascal, Tome III, Paris, 1866. in-8^o.

Problemata de Cycloide, proposita mense Junii 1658.

Quum ab aliquot mensibus, quaedam circa cycloidem, ejusque centra gravitatis, meditaremur, in propositiones satis arduas ac difficiles, ut nobis visum est, incidimus, quarum solutionem a praestantissimis toto orbe geometris supplices postulamus, proposito ipsis praemio, non mercedis gratia (quod absit!) sed in obsequii nostri, aut potius meriti eorum qui haec invenerint, publicum argumentum.

Quae vero proponimus sunt ejus modi. Dato puncto quolibet Z in quacumque cycloide ABCD, ex quo ducta sit ZY basi AD parallela quae axem CF secet in puncto Y; quaeruntur:

[p. 188]

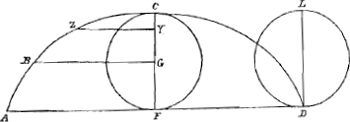
Dimensio spatii CZY; ejusdemque centrum gravitatis; solida genita ex circumvolutione dicti spatii CZY, tam circa ZY quam circa CY; et horum solidorum centra gravitatis.

Quod si eadem solida plano per axem ducto secentur; et sic fiant utrinque duo solida, duo scilicet ex solido circa basim ZY, et duo ex solido circa axem CY genito, cujusque horum solidorum quaerimus etiam centra gravitatis.

Quia vero quaesitorum demonstratio forsan adeo prolixa evadet, ut vix intra praestitutum tempus exsequi satis commode possit, genio et otio doctissimorum geometrarum consulentes, ab his tantum postulamus, ut demonstrent, vel more antiquorum, vel certe per doctrinam indivisibilium (hanc enim demonstrandi viam amplectimur) omnia quae quaesita sunt, data esse: ita ut facile ex demonstratis, quaelibet puncta quaesita ex datis in hypothesibus, possint inveniri.

Et ut apertius mentem meam explicem, nec subsit aliquid ambiguum, exemplo rem illustro. Proponatur, verbi gratia, parabola ABC, cujus axis AB, basis AC,



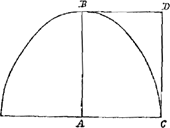
tangens BD, perpendicularis axi AB. Inveniendum sit centrum gravitatis trilinei DCB. Satisfactum esse problemati censerem, si demonstretur, datum esse centrum gravitatis parabolae ABC, necnon et centrum gravitatis rectanguli CDBA, et proportionem hujus rectanguli cum parabola CBA; ideoque datum esse centrum gravitatis quaesitum trilinei CDB. Nam etsi praecise punctum in quo reperitur centrum gravitatis non exhibeatur, demonstratum tamen est datum esse, quum ea ex quibus invenitur data sint; resque eo deducta erit ut nihil aliud supersit praeter calculum, in quo nec vis ingenii nec peritia artificis requiruntur: ideoque non is a nobis calculus exigitur, cur enim in iis immoraremur? Sed tantummodo petimus demonstrari res quae proponuntur datas esse.

Verum doctissimi geometrae prorsus necessarium judicabunt, et ab his postulamus, duarum propositionum, vel duorum casuum integram constructionem, seu integrum calculum.

Primus casus est quum punctum Z constituitur in A.

Secundus, quum idem punctum Z datur in B, in quo transit parallela GB ducta a puncto G, centro circuli genitoris cycloidis.

Quod si aliquis error calculi in his duobus casibus subrepserit, eum libenter condonamus, et veniam quam ipsi peteremus facile promerebuntur.

[p. 189]

Quisquis superius proposita, intra primam diem mensis octobris anni 1658, solverit et demonstraverit, magnus erit nobis Apollo.

Et primus quidem consequetur valorem quadraginta duplorum aureorum Hispanicorum quos ipsi Hispani doblones, et Galli pistoles vocant; vel certe, si mavult, ipsos duplos aureos.

Secundus vero viginti ejusmodi duplos aureos. Si unus tantum solverit, sexaginta solus habebit.

Et quia serio rem agimus, dictos sexaginta duplos aureos illustrissimo domino de Carcavi, regio consiliario Parisiis commoranti apud celsissimum dominum ducem de Liancourt deponi curavimus, qui eos exsolvet statim ac demonstrationes quae ad ipsum mittentur, verae ac geometricae, a viris ab ipso ad id deputatis, judicabuntur. Et quum illustrissimum consiliarium, jam a multis annis virum probum, et matheseos amantissimum agnoverimus, audacter pollicemur rem sincere et absque fallacia exsequendam.

Quod si his circiter tribus elapsis mensibus nullus inveniatur qui quaesita nostra solverit, non denegabimus quae ipsi invenimus, nec aliis invidebimus unde majora jam inventis nanciscantur, et ex quibus forsan apud posteros gratiam inibimus.

Hoc unum restat ut lineae cycloidis descriptionem exhibeamus, a qua brevitatis causa abstinendum arbitrabamur, quum haec linea jam pridem Galileo, Toricellio, et aliis innotuerit; sed quia eorum libri omnibus non sunt obnoxii, ideo hanc ex Toricellio damus.

Descriptio cycloidis. Concipiatur super manente recta linea DA, circulus DL, contingens rectam DA, in puncto D, noteturque punctum D, tanquam fixum in peripheria circuli DL: tum intelligatur super manente recta DA converti circulum DL motu circulari simul et progressivo versus partes A, ita ut subinde aliquo sui puncto rectam lineam DA semper contingat, quousque fixum punctum D iterum ad contactum revertatur, puta in A. Certum est quod punctum D fixum in peripheria circuli rotantis DL, aliquam lineam describet, surgentem primo a subjecta linea DA, deinde culminantem versus C, postremo pronam descendentemque versus punctum A: et talis linea vocata est cyclois.