Oeuvres complètes. Tome II. Correspondance 1657-1659
(1889)–Christiaan Huygens–
[pagina 296]
| ||||||||||||||||||||||
No 560.
| ||||||||||||||||||||||
[pagina 297]
| ||||||||||||||||||||||
Mathematicus, tum ut id ita fiat ut ne fastu suo terreamur, quem virus omne et spurcitiem evomiturum novimus. Sed de his hactenus. De Meibomio et Gallis secus egimus, nec aliter quam ut viros Nobiles et ingenuos tractavimus; nec esse credo quod vel ipsi merito reprehendant. Numquid de me Meibomius in suis adversus Langium scriptis intermiscuit, vel etiam separatim scripsit, ignoro. Sin ita sit, rem gratam mihi facies si id significaveris, et si opus sit scriptum ipsum (quod per Bibliopolam vestrum Dominum BrownGa naar voetnoot6) ad Dominum UnderhillGa naar voetnoot7) Londinensem fieri potest) transmittas: credo enim apud bibliopolas nostros nondum extare. Commercium nostrum EpistolicumGa naar voetnoot8) cum Nobilibus Gallicanis, Fermatio et Freniclo, quomodo sit institutum vides. Ad tricas illas numerosas, ego tantum non invitus accessi, et sero tandem me illis serio applicui, nec nisi provocatus, (quod ex ipsis Epistolis videre est,) illo praesertim quem de omnibus triumphum agere videtur Freniclus in sua ad Solutiones suas Praefatione, cui et occurrendum fortasse non inconsultus censui; quod et fecimus. Sed iniquâ aliquantulum (nisi malè judico) lege, nobiscum et illis decertatum est; (quod et fortasse notabunt alij non moniti;) nempe nihil illi omnino ita solvunt (ne quidem suorum Problematum) ut quis inde doctior vel peritior evadat; saltem non nisi numeros aliquot particulares exhibent quae quaesitis satisfaciunt, methodum interim qua vel illos ipsi vel alij alios exhibeant celantes plane, nec quas a nobis exigunt regulas generales ipsi porrigunt; ad pompam scilicet potius quam ad Matheseos progressum rem instituentes: dum nos contra et responsa damus et responsorum pandimus fundamenta, quod ab illis hactenus ne extorquere possumus. Quid autem inibi meum sit, quid Jllustris Vicecomitis Brounkeri, quanquam non ita facile sit ubique determinare, cum alter alteri non raro, reciprocatis literis, ansam porreximus, suaque mihi plerumque explicanda permiserit, curavi tamen sedulò quae sua sunt sibi asserere; atque, inter alia, Methodum illam quae pagina 71. occurrit, quae est Jllustris Brounkeri magis quam mea (quod ibidem me satis innuisse putaveram) licet eam mihi deinceps reliquerit exponendam; quae et meâ quae praecesserat est multò potior, sed quam ille nondum invenerat quum priorem ipsi exposueram. Neutra tamen tantilli videtur quin ut potior habeatur nudâ numerorum aliquot (quod a Freniclo factum est) expositione. Praesertim cum id utraque ostendat quod non speraverat Freniclus; nempe Analyticen (quam ille sub id tempus in literis huc transmissis contemptui habuit, saltem quod ad hujusmodi quaestiones, et prae sensis suis,) etiam id praestare posse. Et quidem suam (quaecunque sit) five Fermatij five Frenicli methodum nostris inferiorem plane sentio, cum suam neuter hactenus exponere voluerit, quod certo certius essent facturi siquid ipsi vel | ||||||||||||||||||||||
[pagina 298]
| ||||||||||||||||||||||
accuratius vel acutius habuerint. Et simili argumento colligere forsan licebit, Regulam illam generalem quam se pollicetur communicaturum Fermatius pagina 6. modo id desiderem (quod itaque peto pagina 8.) sed quam deinceps perendinat pagina 21. donec ipse exposuerim quid valeam ea de re praestare, et tandem declinat, nec aliud substituit quam Robervallij et Pascalij testimonium, se id praestare posse, pagina 160. traditis a me paginis 45 et 52, vel inferiorem vel saltem nihilo superiorem esse; praesertim cum et quaesiti quod pagina 46. de eodem subjecto reposueram, solutionem declinet. Quod de illatione nostrâ pagina 83. insinuas, non diffiteor verum esse, quod et dudum animadverti; sed cum id in Epistola scriptum fuerat, quae erat bonâ fide inserenda, non visum erat inter edendum immutare. Et quidem ab initio id solum insinuatum ire volebam, Demonstrationis fundamentum potius quam perfectam demonstrationem ibidem traditis subesse; certè vix meliorem putaveram Fermatium ipsum exhibiturum. De Theoremate Fermatij (de potestatibus numeri binariiGa naar voetnoot9) quid statuendum sit, mihi nondum constat. Proprietatem trianguli Amblygonij graduum 120. quam expono pagina 110. &c. brevius posse demonstrari, non ignoro. Sed ego illam ex varijs quae prae manibus erant demonstrationem selegi, quae a trisectione anguli dependet (tanquam elegantem ut ut non brevissimam,) depromptam utique ex tractatuGa naar voetnoot10) quem ante decem annos, de Angulorum sectione, exercitationis causâ conscripseram; ubi consimiles aliorum Triangulorum tum Amblygoniorum tum Oxygoniorum proprietates, simili plane methodo demonstro. Sin breviorem malis, hanc habeas. Sit C continuatio lateris utriusvis, puta A, usque ad perpendiculum P. Erit (propter angulum graduum 60.) C = ½ E. Adeoque PqGa naar voetnoot11) = Eq - ¼ Eq = ¾ Eq. et Q: A + C:Ga naar voetnoot12) = Aq + AE + ¼ Eq. Ergo Tq = Aq + AE + Eq. Quod erat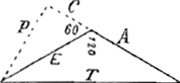 demonstrandum. Sed et eadem facilitate, utrovis modo, demonstrabitur: Si angulus cruribus AE comprehensus, sit graduum 60. quadratum subtensae T est Aq - AE + Eq. Sin esset angulus graduum 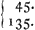 esset Tq = Aq + Eq ±Ga naar voetnoot13) AE√ 2. Et similiter, mutatis mutandis, in Triangulis alijs.
esset Tq = Aq + Eq ±Ga naar voetnoot13) AE√ 2. Et similiter, mutatis mutandis, in Triangulis alijs.
De spatio Conchoidis quod habes; Nempe, quod non animadvertisse videar, spatium | ||||||||||||||||||||||
[pagina 299]
| ||||||||||||||||||||||
illud esse magnitudine infinitum: Omnino secus est. Noveram utique infinitum esse; in data tamen ratione dividi eodem sensu dici poterit, quo parallelogrammum infinitum
 lateribus Aα, Bβ, infinitis interjectum, dicetur in datâ ratione dividi parallelâ recta Dδ quae in data ratione dividit latus AB; vel etiam Parabolam vel Hyperbolam infinitam, diametro dividi in duos semisses. Nec aliud eâ propositione insinuatum volebam. Ad propositionem quam de Cissoide proponis elegantem, quam petis an Infinitorum Arithmetica suppeditare possit; haec habeas. Cum linea Cissoidis ABCb ita sit per constructionem constituta, ut rectam GB (Cissoide et peripheria terminatam, atque ad A, diametri AD terminum tendentem,) bifariam secet NH (diametri AD medio perpendiculariter insistens:) Si ducentur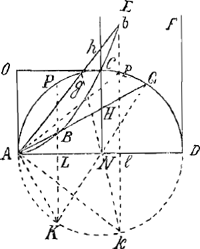 insuper tum GNK diameter, tum rectae KA et KB (quae diametro AD occurrat in L, et peripheriae in P.) ostendit Pappus (libro 3. propositione 5.) propter tum BG bisectam in H, tum GK in N, rectam KB parallelam esse rectae NH; adeoque tum angulum GAK in semicirculo, tum angulos ad L rectos esse: et consequenter, rectas LD, LK (hoc est LP), LA, LB, continue proportionales esse. Quod et similiter ostendetur, de literis minusculis, in Cissoidis continuatione. Ponamus jam rectam AD in partes aequales numero infinitas infinitis punctis L dividi. Erunt itaque omnes AL, ut 1, 2, 3, &c., quarum maxima AD, (quae dicatur D.) Et omnia quadrataGa naar voetnoot14) LK vel LP, ut √: 1 D - 1.Ga naar voetnoot15) √: 2 D - 4. √: 3 D - 9. &c. Cumque sit, ut LK ad LA, sic LA ad LB; Erunt omnes LB (hoc est spatium ADFEB) ut 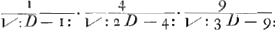 . &c. hoc est, ut . &c. hoc est, ut 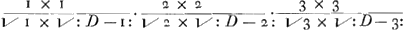 . &c. hoc est, ut . &c. hoc est, ut 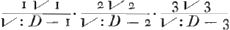 &c. sive &c. sive 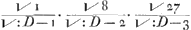 . &c. sive . &c. sive 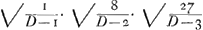 . &c. Hoc est: Omnia quadrata LB sunt series Tertianorum per seriem Primanorum inverse positorum divisa; Jpsaeque LB rectae in quadratorum illorum ratione subduplicata. . &c. Hoc est: Omnia quadrata LB sunt series Tertianorum per seriem Primanorum inverse positorum divisa; Jpsaeque LB rectae in quadratorum illorum ratione subduplicata.
| ||||||||||||||||||||||
[pagina 300]
| ||||||||||||||||||||||
Quod verò series illa infinita, sit tripla seriei √: 1 D - 1. √: 2 D - 4. √: 3 D - 9, &c. (quae est series Radicum quadraticarum seriei primanorum in seipsam inversè ductae.) hoc est, semicirculi; sic colligitur ex principijs Arithmeticae Infinitorum, (quod fusius aliquanto ostendendum erit, quia totum illud negotium de seriebus directis in series inversas ductis, vel per eas divisis, nonnisi parcè illic traditur.) Series primanorum, secundanorum, tertianorum &c. designent a, a2, a3 &c.: item subsecundanorum, subtertianorum &c. √ a, √ 3aGa naar voetnoot16), &c. Si igitur series √ a in seriem a inversam (hoc est, in seriem D - a) ducatur, fiet series D √a - a√a, vel D √ a - √ a3; quae erit ad seriem aequalium ut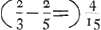 ad 1. (per propositiones 64 et 73 Arithmeticae Infinitorum) Eodem modo, si ducatur eadem series √a, in seriem a2 inversam, hoc est in seriem Q: D - a: vel D2 - 2 Da + a2 fiet series D2 √ a - 2 D a √ a + a2 √ a, vel D2 √ a - 2 D √ a3 + √ a5; quae ad seriem aequalium est ut ad 1. (per propositiones 64 et 73 Arithmeticae Infinitorum) Eodem modo, si ducatur eadem series √a, in seriem a2 inversam, hoc est in seriem Q: D - a: vel D2 - 2 Da + a2 fiet series D2 √ a - 2 D a √ a + a2 √ a, vel D2 √ a - 2 D √ a3 + √ a5; quae ad seriem aequalium est ut 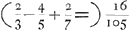 ad 1. (hoc est, in ratione 16/105; vel 16 ad 105.) Et similiter, si eadem series subsecundanorum (sive √ a) ducatur in alias series inversas, prodibunt hae rationes subjectae. Nempe si series √ a ducatur
inverse ad 1. (hoc est, in ratione 16/105; vel 16 ad 105.) Et similiter, si eadem series subsecundanorum (sive √ a) ducatur in alias series inversas, prodibunt hae rationes subjectae. Nempe si series √ a ducatur
inverse
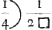 Ga naar voetnoot18). Ga naar voetnoot18). 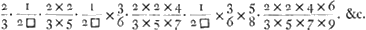
| ||||||||||||||||||||||
[pagina 301]
| ||||||||||||||||||||||
Unde, in praesens negotium, hoc saltem seligendum est, serie √ a et √ a3 invicem ductas inverse, ad seriem aequalium esse ut 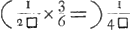 ad 1.
Deinde, ut seriem √ a jam perpendimus, perpendamus similiter seriem √ a3: Ea nempe ducta in seriem a inversam, hoc est in D - a, dat seriem D √ a3 - a √ a3, vel D √ a3 - √ a5, cui convenit ratio ad 1.
Deinde, ut seriem √ a jam perpendimus, perpendamus similiter seriem √ a3: Ea nempe ducta in seriem a inversam, hoc est in D - a, dat seriem D √ a3 - a √ a3, vel D √ a3 - √ a5, cui convenit ratio
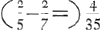 . Et similiter in reliquis, ad hanc formam; Nempe series √ a3 inverse ducta . Et similiter in reliquis, ad hanc formam; Nempe series √ a3 inverse ducta
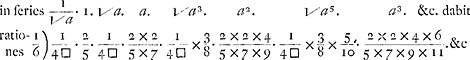 Cum igitur series √ a3 in seriem 1/√ a inverse ducta, hoc est, series √ a3 per seriem √ a inverse divisa, sit ad seriem aequalium ut 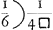 ad 1, hoc est, ut 6/4 □ vel 3/2 □ ad 1: Erit (in casu praesenti) spatium ADFEB ad quadratum diametri AD, ut 3/2 □ ad 1, sive ut 3 ad 2 □. Sed (per propositionem 167. Arithmeticae Insinitorum) semicirculus ACD est ad idem diametri quadratum, ut 1 ad 2 □. Ergo spatium illud est Semicirculi triplum. Quod erat ostendendum. ad 1, hoc est, ut 6/4 □ vel 3/2 □ ad 1: Erit (in casu praesenti) spatium ADFEB ad quadratum diametri AD, ut 3/2 □ ad 1, sive ut 3 ad 2 □. Sed (per propositionem 167. Arithmeticae Insinitorum) semicirculus ACD est ad idem diametri quadratum, ut 1 ad 2 □. Ergo spatium illud est Semicirculi triplum. Quod erat ostendendum.
Similiter (si opus sit) ostendi poterit, Dicti spatij lineam aequilibrij, rectae DF parallellam, ab eadem distare sextâ parte diametri: Jtem, solidum factum ex conversione dicti spatij circa DF ut axem, aequalem esse solido ex conversione semicirculi ACD circa eandem DF, hoc est, semicylindro cujus basis sit idem semicirculus, et altitudo aequalis integrae peripheriae: Jtem, Solidum ex ejusdem conversione circa rectam AO, solidi prioris quintuplum: Solidum vero ex ejusdem conversione circa axem | ||||||||||||||||||||||
[pagina 302]
| ||||||||||||||||||||||
AD, magnitudine infinitum: Centrum denique gravitatis nusquam esse. Nempe sic. Positâ linea aequilibrij AO, erunt momenta rectarum BL, series composita ex serie magnitudinum BL, hoc est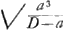 , et distantiam AL, hoc est, a; adeoque series a , et distantiam AL, hoc est, a; adeoque series a 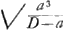 , vel , vel 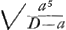 . Cujus ratio ad seriem aequalium, nempe ad momentum quadrati diametri ex puncto D suspensi, sic colligitur. . Cujus ratio ad seriem aequalium, nempe ad momentum quadrati diametri ex puncto D suspensi, sic colligitur.
Series √ a5 inverse ducta 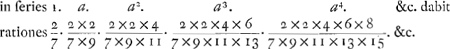 Adeoque, cum series √ a in seriem √ a5 inverse ducta, rationem exhibeat (ut supra) 1/2 □ × 3/6 × ⅝, hoc est 5/32 □: supplebimus interjecta loca, vi analogiae, ad hanc formam. Nempe series √ a5 inverse ducta 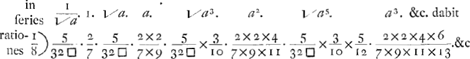 Momenta itaque omnium LB, hoc est, spatij ADFEB in suo situ (respectu lineae aequilibrij AO) est ad momenta totidem AD in distantia AD, hoc est ad momentum quadrati AD ex puncto D suspensi; ut 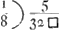 hoc est 5/4 □, ad 1; sive 5 ad 4 □: Adeoque (propter magnitudinem semicirculi ad diametri quadratum, ut 1/2 □ ad 1, vel 1 ad 2 □,) ad momentum semicirculi sic suspensi, ut 5/2 ad 1, sive ut 5 ad 2; vel, suspensi ex N, ut 5 ad 1. hoc est 5/4 □, ad 1; sive 5 ad 4 □: Adeoque (propter magnitudinem semicirculi ad diametri quadratum, ut 1/2 □ ad 1, vel 1 ad 2 □,) ad momentum semicirculi sic suspensi, ut 5/2 ad 1, sive ut 5 ad 2; vel, suspensi ex N, ut 5 ad 1.
Spatium igitur ADFEB in suo situ, aequiponderat quintuplo semicirculi in suo situ, hoc est ex puncto N suspensi, adeoque semicirculo in quintuplo distantiae AN, et consequenter (propter magnitudines distantijs reciproce proportionales) cum spatium illud sit semicirculi triplum, distantia erit distantiae subtripla, hoc est 5/3 AN, vel ⅚ AD; nempe a recta AO; adeoque ⅓ AN vel ⅙ AD a recta DF. Tantundem itaque distat spatij Cissoidalis linea aequilibrij (et, si quod sit, centrum gravitatis) a rectis illis AO et DF. Quod erat ostendendum. Idem eodem modo colligitur, positâ (ab initio) aequilibrij linea DF. Nempe, cum series magnitudinum LB sit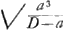 , et distantiarum D - a; est, ex utrisque composita, series momentorum , et distantiarum D - a; est, ex utrisque composita, series momentorum 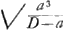 in D - a, hoc est √: a3 in D - a; sive se- in D - a, hoc est √: a3 in D - a; sive se- | ||||||||||||||||||||||
[pagina 303]
| ||||||||||||||||||||||
ries √ a3 in seriem √ a inverse ducta; cui convenit (ut supra) ratio 1/4 □. Momentum itaque dicti spatij in suo situ (respectu rectae DF) est ad momentum quadrati AD, in distantia AD suspensi, ut 1 ad 4 □; adeoque ad momentum semicirculi sic suspensi, ut 1 ad 2: Hoc est, aequiponderat semicirculo suspenso in distantia ½ AD, hoc est ex puncto N seu Centro. Hoc est, Spatium Cissoidale in suo situ, aequiponderat Semicirculo in suo, respectu rectae DF. Et consequenter, cum Spatium Cissoidale sit semicirculi triplum, erit distantia distantiae subtripla; hoc est ⅓ DN, vel ⅙ DA; nempe a recta DF; adeoque ⅚ DA a recta AO; ut prius. Atque hinc statim colligimus, Solidum ex conversione Spatij Cissoidalis ADFEB, ad solidum ex conversione Semicirculi ACD, circa eandem rectam AO, esse ut 5 ad 1; (nempe ut planorum momenta respectu ejusdem rectae AO:) circa rectam autem DF, aequalia esse; (propter aequalia planorum momenta respectu istius rectae.) Atque hoc quidem oppido notandum est; (quod nescio an quispiam me prior indicaverit:) Rationes momentorum linearum vel planorum, respectu cujusvis rectae, et rationes Figurarum ex earundem conversione circa eandem rectam factarum, easdem semper esse. Demonstratio facilis est: quia nempe utraeque ex eisdem rationibus componuntur; nempe Magnitudinum et Distantiarum. Quod unum si animadvertisset Tacquetus, doctrinam suam, (acutam quidem et elegantem) de Cylindricis et AnnularibusGa naar voetnoot19), auctiorem multò reddidisset, fortassis et breviorem. Quippe tum, ad magnitudinem Annuli ex quacunque figura plana circumducta facti determinandam, nil aliud opus esset, quam, ut plani magnitudinem, suique centri gravitatis distantiam a polo seu conversionis axe, perpendat. Est utique Annulus aequalis Prismati, cujus basis est figura genitrix, et altitudo aequalis peripheriae, quae a figurae genitricis centro gravitatis describitur. Sed hoc obiter; quod tibi tamen forte non displicebit. Deinde; si spatium Cissoidale converti intelligamus circa rectam AD, manifestum est, circulos radiorum LB esse in eorundem radiorum ratione duplicata; adeoque et series a3 / D - a, quae ad seriem aequalium, nempe totidem circulos radiorum D seu AD, rationem habet infinitam, adeoque est infinitae magnitudinis. Quod sic colligitur. Series a3 inverse ducta
Cum igitur rationes continuentur (ut patet) multiplicando proxime praeceden- | ||||||||||||||||||||||
[pagina 304]
| ||||||||||||||||||||||
tes per ⅕, 2/6, 3/7, &c.; harum prima multiplicare debet praecedentem per 0/4, quae igitur esset 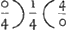 Ga naar voetnoot20). Adeoque series eadem a3 inverse ducta in seriem 1/a, (hoc est, series Ga naar voetnoot20). Adeoque series eadem a3 inverse ducta in seriem 1/a, (hoc est, series 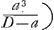 rationem haberet 4Ga naar voetnoot21) ad 0, quae est infinita: ipsumque solidum propterea magnitudinis esset infinitae. Quod item ostendendum erat. rationem haberet 4Ga naar voetnoot21) ad 0, quae est infinita: ipsumque solidum propterea magnitudinis esset infinitae. Quod item ostendendum erat.
Sed et propterea (ut modo ostensum est) momentum plani Cissoidalis ADFEB respectu rectae AD, esset ad momentum quod ratio AD, respectu ejusdem rectae, ut 4Ga naar voetnoot21) ad 0; hoc est infinitum: Et consequenter, cum spatium illud sit magnitudinis finitae, distantia centri gravitatis esset infinita; quod igitur nusquam est. Quod ultimò suscepimus ostendendum. Vides itaque quomodo ex Infinitorum Arithmetica priorem propositionis tuae partem (cum lucro) absolvimus. Reliqua pars, de Spatio ABCO triplo spatij APCO, similiter absolvenda erat: Sed nunc non vacat; metuo etiam ne jam nimius fuerim. Quomodo autem utrumque tu vel inveneris vel demonstraverisGa naar voetnoot22), non ingratum esset audire. Horologij quod misisti specimen gratus accipio: egregium equidem et nobile inventum. Videram prius apud nostros inventum illud penduli Elateri applicatum; sed et innotuit, inventum tuum esse, (an ab ipso artifice, an aliunde, nescio:) pendulum vero istud longitudine tres aut quatuor digitos (si recte conjicio) vix excedebat. Levis autem in circumstantijs immutatio nequaquam poterit invento tuo derogare, quum illud pro cujusque arbitrio fieri potest: Et quidem sive ponderi sive elateri applicetur, ea tamen penduli applicatio utcunque tua erit. Objectionum quas memoras de exiguâ quae adhuc superest inaequalitate, tum ob mutatum penduli arcum; tum etiam ob vim pendulo a pondere illatam, utraque mihi quum primum rem audiveram animo obveniebat: sed et eadem quam et tu adhibes solutio, utramque statim abstulit atque concepta erat; tantillam utique illam esse ut merito contemni debeat. Quam autem suggerit WendelinusGa naar voetnoot23) inaequalitatemGa naar voetnoot24), haud veram esse existimo. Aptaverat autem jam antehac ex nostris | ||||||||||||||||||||||
[pagina 305]
| ||||||||||||||||||||||
nonnemo rotulam suo pendulo quae vibrationes suas numeraret; sed de Horologio ita instituendo non erat solicitus, quod tu egregio successu perfecisti. Ad Saturni tandem observationes deveniendum. Tenue illud commentumGa naar voetnoot25) quod a Joh. Hodierna editum memoras, ut nemini non obvium esset Saturni phases pauculas leviter consideranti, ita nullo modo satisfaciet multiformia illa quae apparent phaenomena penitus intuenti. HeveliusGa naar voetnoot26) ad rem propius accedit, nec satisfacit tamen. Quid Dominus Wren nostrâs, de hoc negotio, ex observatis suis et aliorum collegit, speraveram jam ante tibi communicâsse, si modestia Viri non fecisset ut ipse sua minoris habeat quam par est. Spem tamen fecit ut cum hisce literis aliquid eorum ab ipso accipias. Si autem vel Hodiernae vel Hevelij hypothesin satisfecisse posse putasset phaenomenis Saturni omnibus; jam ante multos annos valuisset vel tales vel etiam exquisitiores hypotheses edidisse. Quaenam autem sit illa tua hypothesis Anagrammate tecta, nos nondum intelligimus. Saturni fasciam, quam et te vidisse insinuas, observavit (quantum scio) primus ante aliquot annos Dominus Gulielmus Ball, Domini Petri Ball Equitis filius, (frater illi quem tibi nuper commendatum dederam,) Telescopio Romano (ab Eustachio de Divinis, ut aiunt, facto) vix ultra 12 pedes Anglicanos longo; Anno 1655: quam ubi Domino Paulo Nelio alijsque aliquot indicaverat, prout erant oculorum acumine vario hi concedebant illi secus; sed adhibitis demum tubis longioribus res statim extra dubium posita est. Audio etiam eundem jam nuper aliquod novum observâsse, sed quid illud sit nondum valeo distincte notare. Cum verò adhuc interroges, quid sibi volet illud in Anagrammate nostro, quasi lunando vehiturGa naar voetnoot27); suspicari subit literas meas, 29 Maij 1656 ad Te scriptas, perijsseGa naar voetnoot28). Jndicaveram utique literis illis, his vocibus id solum intelligi me velle, Saturni comitem eodem plane modo circa Saturnum ferri quo circa terram Luna: puta, ut orbem Lunae integrum magna Terrae orbita secum fert, sic orbita Saturni sui comitis orbem; item Saturni comitem, ut Terrae Lunam, quantum adhuc videre contigit, unicum esse, non, ut Jovis, quaternos; sed nec, ut ansulas, Saturni corpori adjunctum; et quidem ut Luna suas ad Terram phases immutat varie, ita (credibile saltem est, ut ut illud ob distantiam non valeamus hic notare) suas ad Saturnum suus comes: quae omnia Lunandi voce (barbarâ forsan) velim intelligas; cujus tamen sive asperitas sive barbaries adjunctâ voculâ quasi lenienda videbatur. Sed et eisdem literis indicabam neque me neque Dominum Paulum Nelium aliumve ex nostris id velle ut observationis tuae laudi quicquam derogetur; sed illius quam mundo primus patefeceris laudem feras: adeoque et quicquid de hoc Tibi scripseram tamquam inter nos dictum habeas, nec gloriae tuae obfuturum me- | ||||||||||||||||||||||
[pagina 306]
| ||||||||||||||||||||||
tuas: quod identidem repeto; neque enim nobis vel est vel erat in animo tecum de hoc contendere. Sin autem placuerit tractatu tuo quicquam ea de re insinuare, sufficit saltem si innuas (quod et verum est) Dominum Paulum Nelium Equitem Anglum, una cum Domino Wren Astronomiae Professore Londinensi, alijsque, stellulam eandem sub idem tempus saepius vidisse. Verum aliud adhuc, quod forte non suspicaris, latet mysterium. Quod, si spondeas te mihi succensere nolle si dixero me familiariter tecum lusisseGa naar voetnoot29), aperiam. Sed quid haesito? Ego id mihi spondeo tuo nomine: Cum ingenuo siquidem viro rem habeo, et cui ingenui lusus non displicebunt. Rem igitur habe. Anagrammatis illa meiGa naar voetnoot30) expositio non ante facta est quam ego tui expositionem acceperam, cui ego meam datâ operâ conformem reddidi. Quod factum est, non eo animo ut tibi quicquam derogem (neque enim quicquam cuiquam quod eò spectet insinuavi, saltem si te ipsum excipias,) sed ut experimento videas, quàm non absolute securus esse possis aenigmate tuo tectus. Et quidem quum primum Gryphum tuum mecum depositum acceperam, duo statim animo observabantur: Alterum, quod Dominum Paulum Nelium noveram unà cum Domino Wren, de Saturno jam multa observasse, quae ab alijs vix ante observata putabam; et quidem ansam non unam praebuit Epistola tuaGa naar voetnoot31) unde conjicerem de Saturno intelligendum gryphum illum, nec quidem malè conjeci; adeoque nulli injurium fore credidi, si simili interposito grypho honorem sibi suum de observatis varijs Saturni phasibus sartum tectum conservem: Alterum ludicrum erat; nempe ut tibi aliquantum ludendo imponerem, (sed quod deinceps foret exponendum). Noveram utique (nam anagrammata olim non infeliciter tractavi) non incredibilem omnino rem esse, literas quasi fortuito positas (saltem si ea cura adhibeatur ut ex literis frequentius occurrentibus plures ponantur, ex rarioribus pauciores; quam rem mihi familiarem reddiderat, quâ aliquoties occupatus fui, interceptarum literarum Cyphris ut loquuntur scriptarum frequens expositio;) posse non magno negotio ita transponi ut commodum utcunque sensum sustineant, et quidem ut ad quemlibet fere sensum respicere saltem videantur. Et quamvis ingenio forsan ad hoc opus esse dixeris, quam id tamen in praesenti negotio consecutus fuerim, vides, (forsan et miraris.) Ut igitur utrumque simul efficerem, aenigma meum sic institui ut literis quae voces aliquot, varias Saturni phases nobis nuper observatas innuentes, exprimant, alias adjunxi quae quid vellent nesciebam, sed quibus confidebam me postea posse absconditum illud quicquid sit aenigmatis tui exprimere: quod et factum est. Atque jam habes rem totam: Si saltem illud addas, stellulam hanc novam a nostris jam saepius ante conspectam; sed non prius animadverterant planetam esse quam tu id indicaveris: hunc igitur honorem Tibi nos illibatum conce- | ||||||||||||||||||||||
[pagina 307]
| ||||||||||||||||||||||
dimus. Quod te diutius celandum non putabam cum te harum rerum narrationem moliri intelligam; ne ludicrum hoc nostrum tibi sit reapse injurium. Innocuos interim mihi lusus condones. Anonymi Galli Problemata quae memoras de Cycloide, huc etiam delata, pleraque saltem solvimus tum ego tum et Dominus Wren; an omnia tamen possint aliter quam per approximationem Geometricè solvi dubitavimus. Ferunt tamen omnium solutiones jam inde ab Octobris 1. ab authore in Gallia divulgatasGa naar voetnoot32), quaenam autem illae sint nondum audio. Si autem (quod suspicor) Pasca- | ||||||||||||||||||||||
[pagina 308]
| ||||||||||||||||||||||
lius sit qui haec proposuit, cum ille idem (quod etiam intelligo) aliorum omnium quae allatae sunt solutiones interea temporis perlustraverit, tanquam ad hoc a Carcavio delegatus, nescio quam id candide fieri dicatur, cum non omni suspicione vacet se vel inde solutiones aliquas vel solutionum saltem ansas desumpsisse posse: Uti nec omnino candidum videtur, quod horum aliqua jam olim a Robervallio soluta nunc perhibent, et amicis forsan aliquot (privatim, credo,) exposita, et propterea qui eadem jam solverit non invenisse censendum esse; At, inquam, dum ea sibi et suis privata tenuit, nec publice divulgavit; vel debuissent illi haec eadem jam ut cognita exposuisse, non ut jam sub pretio investiganda; vel qui sic proposita jam invenerit non minus censendus erit invenisse, quam ille olim; saltem nisi aliquo pacto a Robervallij inventis hausisse sua censeri possit, (quod jam de Torricellij mensurâ Cycloidis divulgatâ jactitant Galli, nempe se hanc a Robervallio didicisse; quam verè, nescio.) Sed haec, cum alijs, illorum candori permittimus. Superest, ut prolixae tandem Epistolae periodum imponam; et felicia tibi precatus valere jubeam.
Dabam Oxoniae, Decembris 22. 1658. |
|