Oeuvres complètes. Tome II. Correspondance 1657-1659

[p. 349]

N^o 585.
[Bl. Pascal] à P. de Carcavy.
[1659.]
Appendice II au No. 583.

La copie¹⁾ se trouve à Leiden, coll. Huygens.

Resolution ou analise de la proposition de Monsieur Huygens.

Soit vne parabole donnée bIC, dont bC soit la base, aI l'axe.

Il faut trouuer la dimension de la surface du Conoide, descrit par la ligne parabolique tournant au tour de l'axe aI.

Soit vne parabole pareille bDC sur la mesme base et de l'autre part pour ne point brouiller la figure ayant le mesme axe aD quj est aI prolongée.

Jl est demonstré dans le traitté des trilignes²⁾, que pour trouuer la dimension de la surface descritte par la ligne courbe bmD tourné autour de aD jl suffit de connoistre la somme des sinus sur aD; c'est a dire en diuisant la ligne bD en parties egales et jndefinies aux points m, et menant les perpendiculaires mn.

Jl a esté aussy demonstré dans le mesme traitte que pour connoistre la somme de ces sinus mn jl suffit (en diuisant aC en parties jndefinies et egales aux petits arcs egaux mn³⁾ et menant les perpendiculaires gh jusqu'a la courbe) de connoistre la somme des courbes Ch.

Or Monsieur Auzout a demonstré que la ligne courbe entiere C h D, est representée par la somme des droittes b f (en diuisant a E double de a I en vn nombre jndefiny de parties egales) ou a la somme des perpendiculaires f L, quj sont egales aux droittes b f, et lesquelles f L forment le dehors d'vne hyperbole.

1) Cette copie est de la main de P. de Carcavy.

2) Voir l'ouvrage de Pascal, cité dans la Lettre N^o. 560, note 32. cα.

3) L'auteur veut dire: en divisant aC en parties indéfinies et égales, dont le nombre est égal à celui des petits arcs égaux mm.

[p. 350]

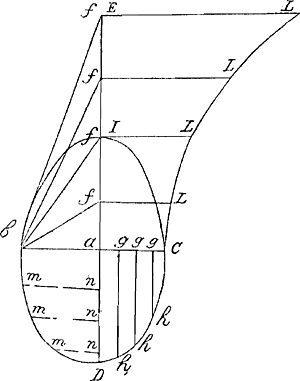
Et de mesme chaque portion D h sera representée par la somme des droittes b f ou f L comprises entre le point I, et chacune des droittes f L c'est a dire que chaque D h sera representée par chaque espace I f L; Et partant chaque portion C h sera representée par chaque espace EfLL.

Donc la somme des C h est representée par la somme des espaces EfLL. c'est a dire par la somme triangulaire des droittes f L a commencer du costé de I. (comme il a esté monstré dans la lettre a Monsieur de Carcauy jmprimée auec le traitte de la Roulette) c'est a dire a la somme des rectangles I f en f L:

Or la somme de ces rectangles est donnée puis que le solide de l'hyperbole touné⁴⁾ au tour de l'axe est donné. Donc la somme des arcs C h est donnée. Et partant aussy la dimension de la surface du Conoide parabolique.

Je ne vous enuoye pas cela pour pretendre aucune part a cette admirable jnuention. Car ie scay trop combien c'est peu de chose de demonstrer ce qu'vn autre a enoncé, outre que cette analyse ne s'estand pas aux Conoides hyperboliques, ny aux spheroides ou la chose me paroist bien plus difficile, ainsy ie n'y penseray pas seullement car ie suis persuadé qu'il y a plustost du blame que de l'honneur a accquerir en trauaillant sur les ouurages d'autruy et principalement quand ils sont traittez par des personnes excellentes comme Monsieur Hugguens⁵⁾.

4) Lisez: tourné.

5) Il y a plusieurs passages dans cette lettre, que de Carcavy semble avoir mal copiés.