Oeuvres complètes. Tome I. Correspondance 1638-1656

[p. 50]

N^o 25.
M. Mersenne à Christiaan Huygens.
8 janvier [1647].

La lettre se trouve à Leiden, coll. Huygens.

Monsieur

i'ay esté assez long temps à deliberer si ie vous escrirois à ce voyage tant parceque ie n'ay pas eu assez de temps pour lire vostre probleme de la corde tendüe, (quoy que ie commence desia de l'admirer si fort, que si iamais vous donnez quelque chose au iour que ie souhaitte que vous l'intituliez Archimedes Batauus) que pour ce que i'attends à vous enuoyer vn traité des centres de percussion qui vient de s'imprimer, en attendant de vous faire tenir par la voye de Mr. vostre pere le reste du liure qui pretend demonstrer tout ce qui concerne non seulement les mouuemens naturels des corps pesans descendans perpendiculairement et sur toutes sortes de plans inclinez, et des mouuemens violens, mais aussi de toutes autres sortes de mouuemens composez en toutes façons. Ie m'asseure que tout cela sera bien digne de vostre examen, dont i'espere que vous me ferez part, nommement en ce qu'il impugne la proportion de l'acceleration par les nombres de Galilée 1, 3, 5, 7, etc. qui est aussi la vostre, et en ce qu'il a beaucoup de choses, qui choquent certains principes de Mr. des Cartes, auquel ie vous prie de faire voir ledit traité, car quand il aura passé par vostre jugement pour y marquer les paralogismes ou fautes s'il y en a contre la Geometrie ou la Philosophie, ie ne croy pas qu'on ayt besoin d'autre decision.

Or attendant que i'aye fait accommoder ce livre, je vous proposeray seulement cette figure d'un triangle de bois ou de fer, ou de telle autre qualité que vous voudrez ou si vous aymez mieux vn plan triangulaire rigide, affin de voir si vostre analyse y pourra donner l'atteinte necessaire.

Soit donc le triangle ABC pendu au point A, en telle sorte qu'il fait aysement ses vibrations de B en I et de C en H, soit la perpendiculaire, ou son axe AF prolongé tant qu'on voudra vers G. Il est certain qu'il y a vn point dans ce triangle où en se remuant et balançant comme i'ay dit, il frape plus fort qu'en nul autre endroit, et ce point se rencontre dans l'axe AF, prolongé si besoin est, il est donc question de le determiner, et il sera ce qu'on appelle le centre de percussion.

De mesme soit le secteur de cercle ABGC, qui se meuve aussi par CH et BI, ou sera

[p. 51]

son centre de percussion? Or ie supose que l'angle BAC est de 153 degrez; et à chaque changement d'angle il est certain que le centre de percussion change auec triangles.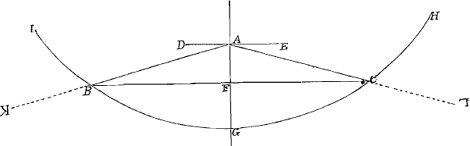

Tournez la figure sans dessus dessous: et imaginez le triangle renuerse CBA suspendu au point F par le milieu de la base, et qu'il se balance vers K et L. Son centre de percussion sera dans l'axe FA, où sera ce? si vous me resoluez cela par raisonnement, eris nobis magnus Apollo.

Ce sera attendant que vous voyiez ce qu'en a dit l'auteur des mouuemens, qui a vn grand genie, mais il n'a point touché ce dernier cas que ie scasche, ni le 3^e, que i'acheve de vous proposer, puisque la mesme figure le permet; soit donc aussi le secteur de cercle renuersé CGBAC, pendu par G et se balançant de B vers K et de C vers L en quel point de GA sera son point de percussion? oubien si vous ne prenez que le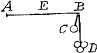



secteur CGBFC, ou sera ledit centre? Celuy qui soudra ces 3 ou 4 cas^a) par raison, deura estre estimé le j^r Geometre de l'Europe à mon auis, et c'est ce qu'on n'a pu faire jusques à present.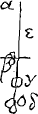

Au reste vous pourrez prendre tel temps qu'il vous plaira pour cela; Et parceque Monsieur vostre pere se plaist grandement à la Musique i'espere que vous prendrez plaisir pour l'amour de luy, de resoudre vne dificulte harmonique que vous experimenterez vous mesme sur vostre Luth, ascauoir pourquoy il faut qu'une chorde de Luth tendüe à vn certain ton, soit tendüe 4 fois dauantage pour monter à l'octaue, attendu que l'octaue n'a sa raison que de 2 a 1. Soit la corde AB attachée au point A et qui passe au point B sur vne poulie; ou si vous aymez mieux, soit vostre Luth vertical αβ, et que la corde attachée à la cheuille α passe par dessus le cheualet d'en bas β, pendant librement en γδ, si le poids γ tendant la chorde à quelque ton que vous remarquez en touchant la chorde en ε, ou E¹⁾ est marqué: pour la faire monter de ton iusqu'à l'octaue il faut y aiouter encore 3 poids, dont chacun soit egal au premier, donc les poids ou tensions doiuent estre en raison doublée des sons. Il semble que cela depend

a) I'ay trouue tout cecy l'an 1664, et bien d'avantage. [Christiaan Huygens.]

1) Dans l'autre figure.

[p. 52]

de la raison des cheualets, car les espaces sont en raison doublée des tensions, voyez si vous la luy pouvez accommoder, ou s'il y a quelqu'autre raison. Et si quand la



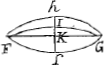corde de vostre Luth FG est tirée iusques à H par exemple, et qu'elle retourne iusques à L, et qu'elle reuient iusques à I, et ainsi des autres retours iusques à la fin, si, disie, ces lignes de retour HL et LI etc. sont en proportion geometrique, geometriques [sic] ou quelquautre. Or ie veux vous faire part de ce qu'a produit icy depuis quelque temps nostre Academie Mathematique, et puisque vous aymez les centres de pesanteur ou grauité,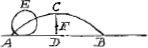



dont celuy de la figure que nous nommons trochoide, ou cycloide, qu'est la courbe ACB, descrite par le cercle AE faisant par son tour entier sur le plan AB la ligne ACB en l'air, et ADB egale à sa circonference. Le centre est au point F, lors que de F a C il y a 8²⁾ parties et de F à D 5. Si vous imaginez ceste figure ACBD torne autour de sa base AB, elle fait vn solide qui est au cylindre de mesme hauteur et dont le diametre est AB, sous sesquiseptieme³⁾: si la mesme figure torne autour de son axe CD, le solide engendré n'est pas à son cylindre comme 11 à 18, ainsi qu'auoit pensé l'excellent Torricelli⁴⁾ de florence, mais en voicy la veritable proportion.

Si ex tribus quadrantibus quadrati dimidiae basis, dematur tertia pars quadrati altitudinis, erit vt reliquum ad ipsum dimidiae basis quadratum, ita solidum Trochoidis circa axem conuersae ad cylindrum eiusdem basis, eiusdemque cum ipso solido altitudinis.

C'est pourquoy ie vous prie de corriger ainsi à la fin de l'Errata de mon Liure que vous citez, ce que i'auois aporté de Torricelli de 11 ad 18.

I'aioute la maniere de marquer auec vne seule ouuerture de compas vn espace courbe sur vn cylindre egal à vn quarré.

Soit le quarré donné A, faites vn cylindre, dont le diametre de la base EF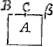



soit egal à la moitié du coste Bβ, ascauoir BC, qui soit EF. Si vous ouurez vostre compas comme EF, et que vous le mettiez sur quelque point du cylindre que vous voudrez, comme en G, sur lequel la pointe estant fichée mettez l'autre jambe sur le contour de ce cylindre qui ira juste iusqu'au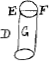



milieu de l'autre costé et luy faites faire le tour iusque à revenir en G, l'espace qu'il aura circonscrit du cylindre sera egal audit quarre. Ce qui a esté icy demonstré.^b)

2) Lisez: 7.

3) Sesquiseptième est 1 + 1/7 = 8/7 (Boethius). Sous-sesquiseptième est donc ⅞.

4) Evangelista Torricelli naquit le 15 octobre 1608 à Piancaldoli et mourut le 25 octobre 1647 à Florence. Disciple de B. Castelli, il sut appelé par Galilée à Florence, en octobre 1641, et assista celui-ci avec Viviani jusqu'à sa mort, le 8 janvier 1642: depuis il y resta comme professeur de mathématiques au collège et comme philosophe du Grand Duc Ferdinand II.

b) Il faut que le compas ayt ses iambes crochües pour bien faire cela, comme ceux dont on mesure les globes. [Mersenne.]

[p. 53]

L'on a aussi trouue le centre de grauité de chaque partie de la superficie d'une sphere, en prenant les parties comme des costes de melon de pole à pole. Et la surface d'un spheroide egale à la surface d'une sphere. Ce que iay voulu vous escrire affin de vous faire part de nos petites nouueautez, et de vous tesmoigner le grand estat que ie fais de vostre excellent esprit.

Je m'asseure qu'aprez auoir vû l'auteur que ie vous enuoye des centres de percussion, vous renchairez dessus, et que vous trouuerez quelque regle plus excelente, ou plus exquisite: et si vous y aperceuez des paralogismes vous me ferez plaisir de m'en auertir.

Si l'on peut trouuer le centre de grauité des 2 susdites solides de la roulette, ou trochoide, l'on aura la quadrature du cercle, que prouue vn P. Jesuiste Vincentio⁵⁾ qui la faite imprimer à Anuers⁶⁾ vous l'auez desia peut estre, ie brusle d'en scauoir vostre iugement si tost que vous aurez examiné son memoire.

Je veux encore icy aiouster le centre de pesanteur de la demie circonference du cercle si vous l'imaginez vniformement pesant: Continuez dans l'un & l'autre quart la quadratrice BEC, qui passe par les extremitez de cette demie circonference, et qu'elle ayt le mesme centre de grandeur A qu'a ladite demicirconference et le mesme axe AE, et le point E sera le centre de grauité de la mesme demiecirconference.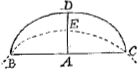

Le Jesuiste susdit promet aussi la quadrature de l' hyperbole, si son liure est en vente à Anuers, ie m'assure que si vous priez Monsr vostre pere de vous le faire venir promptement, vous l'aurez jncontinent et m'en apprendrez ce qui en est.

Vous ferez aussi auec luy qu'il vous face venir d'entre les mains du Sr. Tassin au plustost le volume entier du mouuement duquel j'ay choisi ce que vous en recevrez à ce voyage, et puis vous me ferez scauoir vostre aduis sur le tout.

Enfin, pour acheuer ce papier, on a trouvé d'vn coup, ou d'une ouuerture de compas appliqué sur vn cylindre droit, vne partie de sa courbure ou surface egale à la surface entiere courbée d'un cylindre oblique, ou scalene.

Je croy que vous ne serez pas marry, que ie vous mette icy la methode de trouuer vn lieu entre les nombres où il y ayt vn espace de 100000000000 nombres, ou tel autre que vous voudrez, dont nul ne soit premier.

Il faut multiplier les vns par les autres tous les nombres premiers, moindres que

5) Gregorius a Sancto Vincentio, né à Bruges le 8 septembre 1584, mourut à Gand le 27 janvier 1667. Il était Jésuite, étudia à Rome, devint professeur de mathématiques à Prague (1625), puis, quoique instamment sollicité de venir en Espagne comme précepteur de Don Juan d'Austria, fils de Philippe IV (1631), il retourna en Belgique, où il résidait à Gand. Il nous a laissé plusieurs ouvrages imprimés et 13 volumes de Mss., qui se trouvent à la Bibliothèque Royale de Bruxelles.

6) Gregorii a S^to Vincentio Opvs Geometricvm Qvadratvrae Circvli et Sectionvm Coni Decem libris comprehensum. Puis un beau titre gravé, où dans le milieu sur une peau de lion: Problema Avstriacvm plus vltra Qvadratvra Circvli. Auctore Gregorio A S^to Vincentio Soc. Iesu. et au dessous: Antverpiae, Apvd Ioannem et Iacobvm Mevrsios. Anno m.dc.xlvii. in-folio.

[p. 54]

100000000000, en commencant par 2, si au produit on aioûte 1, ce sera terminus a quo.

Mais parce que cela est trop loin prenez l'exemple de 10, il faut multiplier tous les nombres premiers moindres que 10, ascauoir 2, 3, 5, 7., dont le produit est 210, auquel 1 aioûté, nous auons 211, ioignez 10, ce sont 221, et partant les 2 nombres entre lesquels il y a 10 nombres sans aucun premier sont 211 et 221 differents de 10.

Oubien si de 210 vous ostez 1, reste 209, duquel 10 osté, reste 199, entre lesquels il n'y a nul nombre premier.

Pour trouuer vn nombre premier plus grand qu'un nombre donné, par exemple, qu'un milion, il faut prendre la suite des nombres premiers, qui surpassent de l'unité les nombres de l'analogie de 2⁷⁾, et l'on trouuera la 256_e puissance augmentée d'un qui sera le nombre premier qui surpassera de beaucoup ledit milion.

Mais ces petites gentillesses de nombres sont trop scabreuses pour vous en entretenir. la Geometrie est plus ioyeuse et ie vous demande pardon de ma grande longueur, et encore plus pour ma mauuaise escriture⁸⁾. Mon retour est à Monsieur vostre pere, qui me fait la faueur de lire mes pieds de mouche: c'est à luy s'il y a quelque mot difficile, que vous vous addresserez s'il vous plaist.

Sur ce que ie vous ay dit de la tension quadruple de la corde harmonique pour la faire monter à l'octaue, il me vient de ressouuenir [?] que i'en auois traité dans la balistique proposition 36. dont la lecture vous fera peut estre venir la veritable demonstration dans l'esprit. Il faut seulement y corriger les lettres capitales page 129 ligne 14, ad B, il faut ad E. page 130, ligne 25 rationes et non rectas. page 132 L 18 necessaria. L 21. AGF. L 25. au lieu de CD vers BF, il faut BE, vers CF.

Certes la 35, et la 37 proposition meriteroient bien vostre examen, car ie ne vais quasi qu'en tremblant, de peur de faire tort à la verité: ne nuisant jamais les experiences, qui doiuent seruir de phenomenes; et ie croy auoir faict en cela plus sincerement que si i'eusse construict des demonstrations de bibus, comme l'on dit: tant y a qu'il y a assez de preparation pour exercer vn bon esprit.

Dans la 38 proposition vous verrez les difficultez de receuoir le principe dont vous vous estes serui en vostre j^e demonstration, ascauoir qu'un mobile se mouueroit tousiours de mesme vitesse dans le vuide, dont il auroit este poussé au commencement.

Et outre ce que i'en dis en ce lieu là, l'on vous peut encore obiecter qu'une pierre estant iettée en haut perpendiculairement, ne deuroit jamais retomber, d'autant qu'estant arriué au dernier point où elle se trouue en equilibre auec sa pesanteur,

7) L'auteur veut indiquer des nombres de la forme 2²ⁿ + 1.

8) La qualification m'a rien d'exagéré; l'écriture de Mersenne est une des plus mauvaises qu'on puisse rencontrer. Ce n'est qu'avec beaucoup de peine que les personnes les plus exercées dans la lecture des autographes parviennent à déchiffrer son manuscrit, rendu plus inintelligible encore par le style et l'autographe peu corrects. Aussi les crochets [] de notre texte n'indiquent que trop souvent qu'on n'a pas pu arriver à une solution tout à fait sûre de l'énigme que présentait quelque mot indéchiffrable.

[p. 55]

la force du mouuement qui la conduit en haut, n'a plus de contraire en cet equilibre, donc elle ne le doit point perdre: donc elle ne doit point retomber ce qui est contre l'experience, car de dire que la pesanteur agisse en ce point non comme 1, mais comme 3 et 5, c'est contre l'experience, autrement vn plomb pendu à vn filet, romperoit bien tost le filet en pesant comme 1, et surtout[?] 3, 5, etc. contre l'experience: de dire que c'est l'air ou autre matiere perpetuellement descendante et tournante qui abate et oste la pierre montée à ce point d'équilibre, c'est deuiner sans le voir. Et partant vostre demonstration manque de principe, oûtre que vous ne prouuez par induction que le graue passe par tous les degrez de tardiuité: et voyez qu'au mesme moment que nous laschons vne pierre en bas elle va viste.

C'est chose bien estrange que nous voyions si peu dans la physique, et qu'il y en ayt tant qui disent, ou se vantent de voir si clair dans les choses de la religion, qui depend de ce que nous pouuons beaucoup moins aprocher que ce que nous venons de dire des choses physiques. Il n'y a remede il faut essayer d'auoir patience, puisque la diuine prouidence nous a mis dans cet estat de vie, qui ne depend nullement de nous puisque nous nous trouuons sur la terre sans scauoir qui nous y a mis et d'où nous sommes venus, si on ne nous l'apprend 3 ou 4 ou 8 ans aprez.

Je prie Dieu Monsieur, de vous conseruer toute cette année en tresbonne santé, et que vous soyez l'Apollonius et l'Archimede de nos iours, ou plustost du siecle à venir, puisque vostre jeunesse vous peut donner vn siecle entier.

Vostre tresaffectionné serviteur Mersenne, M.

Ce 8 du nouuel an.

Si vous prenez la peine de lire la 38 proposition, ie vous prie d'y corriger cecy. p. 136 L 24, accenseri tout en un mot, p. 137 L 2 observationes. L 12 explosione L 16, pilas maiores eâdem ac minores. L 29 globus, curvatus proportionaliter. p. 138, L 3, 2200 au lieu de 2000, L 9 au lieu de ferè horae dimidiae spatio, mettez multo tempore. Je vous prie aussi qu'à la 39 proposition qui est mal marquée 35, et qui est la derniere, à la page 139 L 14, vous effaciez tout ce qui est depuis Habet iusque à secundum; parce que i'ay experimenté que dans l'espace de cent toises qui est la plus grande portée horizontale des meilleures arquebuses, la bale arriuera au mesme moment que le son: ce qui me fait necessairement conclure que la bale est du moins à 50 toises, quand le son commence a se faire: car autrement il viendroit bien plustost a l'oreille que la bale, puisque le son fait 230 toises dans 1″. et la bale n'en fait pas 150 dans ce mesme temps.

A la preface generale L 5 et 6 lisez DA sesquidigiti, hoc est octans pedis. pag. 86 Phaen. Mechan. L 2 lisez potentia, resistentia. L 18 et 19, 22464. Il y a page 85 et ailleurs des nombres à corriger, c'est [?] chose horrible d'auoir affaire a des mauuais imprimeurs.

[p. 56]

Excusez si ie barbouille encore cette page, affin de restituer les vrays nombres de la page 85 des mechaniques. L. 16. propiùs L. 30. 26 au lieu de 50. L. 31. 17, non 13. L. 32. 49 non 338. L 33.7 au lieu de decimo tertio. L. 34.7 pour decimi tertii L. 37. 49 pour 338. neque si fuerim Hercules, possim omnes erratorum hydras calami numerorum seu claua delere.

p. 86 vltima linea, scribatur cylindrus 26 hexapedanus,.....cum interuallo crassitudinis et materiae erit paulo 312 librarum. Et tout de mesme page 87. L. 4. 26 et 312 pour 338 et 2648 et L 14. 312.