Oeuvres complètes. Tome II. Correspondance 1657-1659

[p. 170]

N^o 483.
Christiaan Huygens à [J. Wallis].
avril 1658¹⁾.

La minute se trouve à Leiden, coll. Huygens.

1658 Aprili.

^a)b)

APE est Cissoides Dioclis. ACB circulus à quo genita est. semper nimirum AC ∞ EF. Dico spatium AVPEFB aequari triplo segmento CBT + ∆ ^o ACB. ∠ MBH ∞ BAC. BM ∞ AB. triplum segmentum CBT + ∆ ^o ACB ∞ sectori BKM + spatio HXMK. nam fegmentum CBT seu HMX ∞ spatio HXMK.

1) Nous insérons cette pièce sous la date qu'elle porte dans les ‘Adversaria’. Cependant, elle n'a pu être envoyée à Wallis que plus tard, à une époque que nous n'avons pu déterminer exactement. En effet, au lieu cité dans notre note 6 on lit:
Hanc Cissoeidalis Spatii mensuram me primus monuit (sed absque demonstratione) Vir Nobillissimus Dominus Christianus Hugenius (acuti & sagacis ingenii Vir) literis ad me datis 6^o. Augusti 1658 [probablement la lettre N^o. 512 du 6 septembre].
Une lettre de Wallis du 1^er janvier 1659 indique qu'il venait de recevoir cette lettre; d'autre part il résulte d'une lettre de Chr. Huygens, datée du 31 janvier 1659, que celui-ci avait déjà envoyé à Wallis cette démonstration. Par conséquent, elle doit avoir été transmise à Wallis entre le 6 septembre 1658 et le 31 janvier 1659.

a) Premittenda propositio, quod sectori BKM potest inscribi et circumscribi figura dentata ita ut altera alteram excedat spatio minore quolibet dato. [Chr. Huygens].

b) Quidsi semicirculus BHM cum sectore BGM⁴⁾ separetur a reliquis. Et eaedem literae adscribantur quae in ACB? [Chr. Huygens.]

4) Lisez: BKM.

[p. 171]

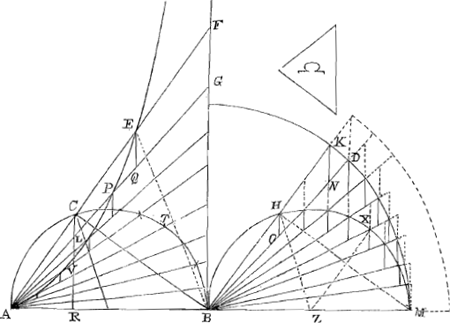
∠ HZM ∞ 2 ∠ HBM. e²⁾ sector ZHM ∞ ½ sectori BKM. e²⁾ sector ZHM ∞ ∆ BHZ + spatio HXMK. auferantur aequalia hinc ∆ BHZ, inde ∆ ZHM. fit spatium HXMK ∞ segmento HMX.

Ergo ostendendum quod spatium AVPEFB ∞ sectori BKM + spatio HXMK. si dicatur spatium cissoidis hisce minus esse; sit excessus horum Ω. Et inscribatur sectori BKM figura ordinatè, ut duplum omnium trilineorum KND sit minus quam Ω. et spatio Cissoidis figura inscribatur ex totidem trapezijs. Ostenditur trapezium EFGQ ∞ ∆ BKN + trapezio HN. est enim trapezium EG ad ∆ ACL ut FG + EQ ad CL, (quia eandem habent altitudinem) hoc est ut FA + AE ad AC. hoc est ut AF + FC ad AC. hoc est ut AB + BR.³⁾ RA. Ergo componendo, trapezium EG + ∆ ACL ad ∆ ACL ut 2AB ad AR. hoc est ut 2 quadratum AB ad quadratum AC. sive ut 2 quadratum BK ad quadratum BH. hocestut 2 ∆ BKN ad ∆ BHO. Sed ∆ BHO ∞ ∆ ACL. ergo trapezium EG + ∆ ACL aequale erit 2 ∆ BKN.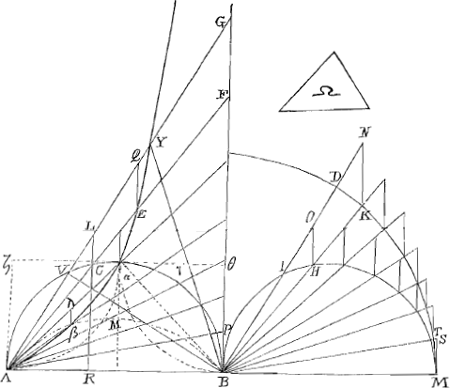



^c)d)

Et ablato hinc ∆ ^o BHO, inde ∆ ^o ACL, manet ∆ BKN + trapezium HN aequale trapezio EG. et similiter de caeteris. Ergo figura in sectore inscripta + trapezijs omnibus HN ∞ figurae in spatio cissoidis inscriptae. Sed figura in sectore assu-

2) C'est le signe pour: ergo.

2) C'est le signe pour: ergo.

3) Ce point signifie: ad.

c) A côté de cette figure on trouve encore
B α β A B ∞ 3 B α γ. Sed ⌓ A α B - B α β A B - B α γ ∞ A V α β A ⌓ A α β - 4 B α γ ∞ A V α β A.
Sed ⌓ A α β - 4 B α γ ∞ ▭ ζ B ÷ ⌓ A α B, Ergo etc. [Chr. Huygens.]

d) Literae F et E, ubi G et Y, ponendae, quia rursus vocandum spatium ut prius. item K et H in locum N et O. [Chr. Huygens.]

[p. 172]

mens omnia KND, itemque trapezia HN assumentia omnia KND; ista omnia simul addita superant sectorem + spatio HXMK. Ergo figura in sectore + trapezijs HN hoc est figura in cissoide assumens spatium Ω, longe superabit sectorem + spatio HXMK. sed ipsum Cissoidis spatium + Ω aequatur ex hypothesi sectori BKM + spatio HXMK. Ergo figura in Cissoide ipso Cissoidis spatio major erit. quod absurdum.

Dicatur jam spatium AEYGB majus sectore BDM + spatio IHMD sitque excessus Ω. Circumscribam jam sectori figuram. ut omnia DKN bis sumpta sint minora excessu Ω. Et ex totidem trapezijs circumscribam spatio Cissoidis. Sicut antea ostendetur trapezium EG ∞ ∆ BKN + trapezio HN. Ergo tota figura circumscripta Cissoidi aequalis circumscriptae sectori + omnibus trapezijs HN^e). Sed ab his si demantur bis omnia trilinea DNK, residuum minus erit quam sector BDM + spatio IHMD. (nam primum auferendo omnia DNK à circumscripta figura sectori, relinquitur sector BDM: at eadem DNK auferendo à trapezijs HN, residua omnia simul, minora sunt spatio IHMD: quin additis rursus OHI, omnia simul aequantur demum spatio IHMD.) Ergo si ab his ipsis, à figura nimirum circa sectorem + trapezijs NH hoc est à figura circumscripta spatio Cissoidis, auferatur Ω, reliquum multo minus erit sectore BDM + spatio IHMD. sed spatium ipsum Cissoidis dempto Ω aequale dicebatur his ipsis. ergo Cissoidis spatium majus erit figura sibi circumscripta, quod absurdum.

Hoc demonstrato quod spatium AEYGB ∞ 3 segmento B V C + ∆ A V B, facile ostendetur spatium infinitum AEYBG aequale triplo semicirculo A V B.

Item quod spatium AEYB ∞ triplo segmento B V C^f)

e) NB. quod ultimum in figura circumscripta Cissoidi est ∆ APB (et non trapezium) aequale ∆ ^o BSM in sectore. [Chr. Huygens.]

f) J'ay envoiè a Monsieur Sluze⁵⁾ la demonstration de cecy; mais cellecy est plus belle.
Je l'ay envoiée a Monsieur Wallis qui l'a fait imprimer dans son traitè de Mechanique⁶⁾. [Chr. Huygens.]⁷⁾

5) Il semble que Huygens ait ajouté toute cette note plus tard, et qu'elle ait rapport à la Lettre No. 487.

6) Cet ouvrage fut imprimé plus tard sous le titre:
J. Wallis Mechanica: sive, de Motu, Tractatus Geometricus. Partes I et II. Oxoniae 1669, Londini. 1670, in-folio.
Huygens indique ici la Pars II, Cap. V. Prop. XXIX. Scholium, où suit la ‘Demonstratio D. Hugenii’ (Voyez J. Wallis, Opera Mathematica, Oxoniae, 1695, in-folio, Vol. I, pag. 906.)

7) La dernière phrase a été écrite au crayon, de la main de Chr. Huygens.

4) Lisez: BKM.

5) Il semble que Huygens ait ajouté toute cette note plus tard, et qu'elle ait rapport à la Lettre No. 487.

6) Cet ouvrage fut imprimé plus tard sous le titre:
J. Wallis Mechanica: sive, de Motu, Tractatus Geometricus. Partes I et II. Oxoniae 1669, Londini. 1670, in-folio.
Huygens indique ici la Pars II, Cap. V. Prop. XXIX. Scholium, où suit la ‘Demonstratio D. Hugenii’ (Voyez J. Wallis, Opera Mathematica, Oxoniae, 1695, in-folio, Vol. I, pag. 906.)

7) La dernière phrase a été écrite au crayon, de la main de Chr. Huygens.