Oeuvres complètes. Tome II. Correspondance 1657-1659

[p. 178]

N^o 487.
Christiaan Huygens à R.F. de Sluse.
28 mai 1658.

La minute et la copie se trouvent à Leiden, coll. Huygens.
La lettre est la réponse au No. 486. R.F. de Sluse y répondit par le No. 489.

Slusio.

Nobilissime Domine

Quod et tibi valetudinem pristinam post brevem αῤῥωςίαν restitutam esse scribis quodque de mea solicitè inquiris utrumque est gratissimum. Ego ijsdem plane incommodis vexatus fui quae tibi accidisse refers, et mecum omnes qui in domo nostra imo in tota urbe morantur. Sed paucos dies morbus mihi abstulit. Plurimos vero negotia molestiae plena quibus, nescio quam bene, me immiscui. et quorum causa plusculos jam dies hic contrivi. Ita aliquamdiu feriari coactus sum a jucundissimis studijs illis quibus nostrum stat commercium. Demonstrationem quam petebas perfectam ac numeris omnibus absolutam tibi mittere constitueram, sed

[p. 179]

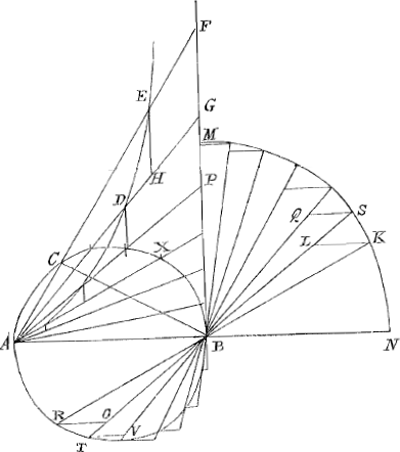
quoniam illa uberius otium requirit, neque adversaria nunc ad manum sunt e quibus concinnanda foret, compendium interim quoddam seu rudimentum potius demonstrationis non insubtilis quod vix tandem in mentem revocavi, hic adscribam. ACB est circulus e quo ortum ducit linea Cissoides ADE. Circulum tangit BF perpendicularis diametro AB. Dixi igitur spatium infinitum inter curvam ADE, et rectas AB, BF interjacens triplum esse semicirculi ACB. Quod ut fiat manifestum ducatur quaelibet ACEF, quae abscindat e dicto spatio partem ADEFBA. Sit autem BMN quadrans circuli radio BN aequali BA descriptus, sumptoque arcu BR aequali BC ducatur recta RBK. Ostendam itaque portionem abscissam ADEFBA aequalem esse utrisque his segmento circuli BVR sive BXC et sectori BKM. Quod cum semper ita se habeat, quomodocunque ducatur ACEF, facile hinc perspicies infinitum tandem quod dixi spatium aequari semicirculo ACB et sectori integro BMN, ideoque semicirculi ACB triplum esse. De spatio autem abscisso ut demonstretur, arcum CXB in particulas aequales diuido, perque diuisionum puncta eductis ut vides rectis ADG &c. figuram quandam spatio ADEFB inscribo è trapezijs EG, DP &c. compositam. arcus BR in totidem partes secatur, atque eductis per B rectis tot quoque partes aequales facit in sectore BKM. Sint RO, TV item KL, SQ parallelae AB. Jam trapezium EG aequale ostendo triangulis inter se oppositis ROB, BKL; item trapezium DP, duobus triangulis TVB, BSQ &c. Unde reliqua facile colliges. Quod trapezium EG aequetur ∆ ^is ROB, BKL sic demonstro. Quadratum AF aequatur quadratis FB, BA, quorum FB aequale quadratis FC, CB. Ergo quadratum AF ∞ quadratis tribus FC, CB, BA. Quamobrem etiam triangulum super AF descriptum nimirum AFG aequabitur ternis simul triangulis huic similibus super rectis FC, CB, BA descriptis. Hoc est super rectis AE, BR, BK. Est enim AE aequalis FC ex proprietate Cissoidis, et ex constructione BR ∞ BC, et BK ∞ BA. Sunt autem super rectis AE, BR, BK triangula ipsi AFG similia AEH, BRO, BKL. Ergo haec tria aequalia triangulo uni AFG: et ablato utrinque triangulo AEH, relinquitur trapezium EG aequale triangulis duobus BRO, BKL, quod erat propositum. Jam ex hoc caetera secundum ea quae praemisi collige. Perfecta demonstratio sieret deductione ad impossibile, et figuras etiam circumscriptas requireret quas hic tantum inscriptas considerauimus. Hanc interim rogo ut boni consulas, tibique habeas, neque alij concredas ulli. Hagae me accessit bis terve Juvenis Ornatissimus Dominus Brunetti Florentinus e Gallia adveniens et hinc in Germaniam profectus, is se Torricellio magistro usum dicebat quanquam ad breve tempus, tecumque Romae familiaritatem contraxisse. De te itaque plurimus nobis sermo talisque perpetuo quo tibi dextram aurem tinnijsse verisimile sit.

Vale Vir Eximie et me ama.

Amstelod. 28 Maj. 1658.

Praetium promiseras methodum quandam qua tangentes curvarum linearum

[p. 180]

ducuntur. sed minori tuo incommodo facies et quod mihi longe sit acceptius si duarum mediarum constructionem ope Ellipseos impertieris quam mea illa olim ad te missa compendiosiorem asserebas.

Qua via ad Dominum Hodiernam literas in Siciliam mittere possim an ea qua meae venerunt an alia, si nosti, quaeso mihi significa. debeo enim responsum neque hic ulla adest occasio¹⁾.

1) Chr. Huygens semble avoir biffé cette dernière phrase.