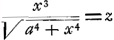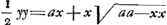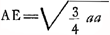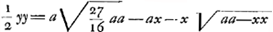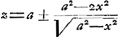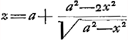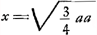Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–
[pagina 249]
| ||||||
No 2736.
| ||||||
§ IGa naar voetnoot2).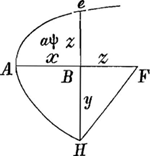 Subnormali BF àequalis est Be applicata in curva Ae, et sic ubique, jam ½ yy sive ½ qu. BH aequatur spatio AeB ex Barovij theor.aGa naar voetnoot3). Quaerimus hic, ex cognita quantitate spatii AeB, expressa per x, a et b, quaenam sit aequatio curvae Ae, quae nempe exprimat relationem inter x et z, hoc est inter AB, et Be. | ||||||
Exemplum 4m Hub. Huighenij ZelandiGa naar voetnoot4).NB. Pono x pro illius y. Et ½ yy pro illius aψGa naar voetnoot5) ut ad Barovij theorema examinem.
| ||||||
[pagina 250]
| ||||||
9b2y4+12a3byy-12aax4-4x6=0. Hinc incepitGa naar voetnoot7); eamque ita egregie ordinavit ut in quadrabilem ita simplicem perduceret. Subtang.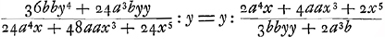 , subnormalis. , subnormalis.
| ||||||
[Exemplum 15.]Erat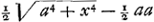 non curtatum. Si x=o, fit y=o. Si x=aliquid, fit ½yy=aliquid. non curtatum. Si x=o, fit y=o. Si x=aliquid, fit ½yy=aliquid.
| ||||||
[pagina 251]
| ||||||
§ IIGa naar voetnoot9).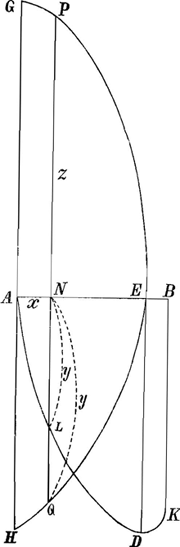 4x4-3aaxx=aazz-xxzz+2axxz-2a3z; aequatio curvae EG quadrabilisGa naar voetnoot10), cujus applicatae sunt subnormales curvae ADK usque ad D ubi subnormalis=o. Eaedem vero applicatae sunt etiam subnormales curvae EH, cujus aequatio initio pag. sequentis ponitur. Sic omnis curva ex duarum diversarum curvarum subnormalibus applicatas constitutas habet. Et hoc fundamento nititur Curtatio nostra. Nam ex Barovij Theoremate erit spatium AGPN aequalem ½ qu. NL. Et ex eodem erit spatium PEN=½ qu. NQ. Est autem totum spatium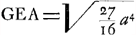 , cum nempe , cum nempe 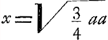 sive AE. Ergo cum posito AN=x, sit spatium AGPN=ax+x sive AE. Ergo cum posito AN=x, sit spatium AGPN=ax+x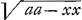 =½yy ubi y est NL: erit spat. =½yy ubi y est NL: erit spat. 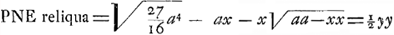 cum y est NQ.
Haec vero est non curtata quadratura quam voco: illa vero cum y est NQ.
Haec vero est non curtata quadratura quam voco: illa vero 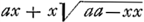 curtata; ex quibus eandem utrobique curvam GE quadrabilem inveniri necesse est. curtata; ex quibus eandem utrobique curvam GE quadrabilem inveniri necesse est.
Curtatio nostra utilis ad formandas quadra- | ||||||
[pagina 252]
| ||||||
turas ex quibus curva paucorum terminorum; ut patet comparatione hujus exempli cum illo quod pag. sequen.Ga naar voetnoot11) ubi tamen curva eadem utrobique oritur. |
|


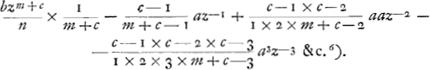
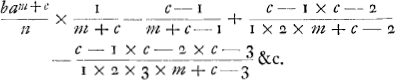
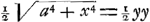 ; nusquam fit y=o.
; nusquam fit y=o.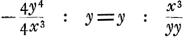 subnorm.=z
subnorm.=z