Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 374]

N^o 2782.
Christiaan Huygens.
21 novembre 1692.
Appendice V¹⁾ au No. 2777.

La pièce se trouve à Leiden, coll. Huygens.

21 Nov. 1692. hanc e tenebris erui quadraturam.

1) Cet appendice, que nous avons emprunté aux pages 141-145 du livre H, contient la quadrature du folium de Descartes x³+y³-bxy=0. Il a été reproduit par Uylenbroek, Excercitat. math., Fasc. II, p. 154-158, sous un arrangement un peu différent. Nous avons ajouté une division en paragraphes.

§ I²⁾.

e³+u³=eub. Aequatio curvae a Cartesio, Huddenio et aliis multo examinatae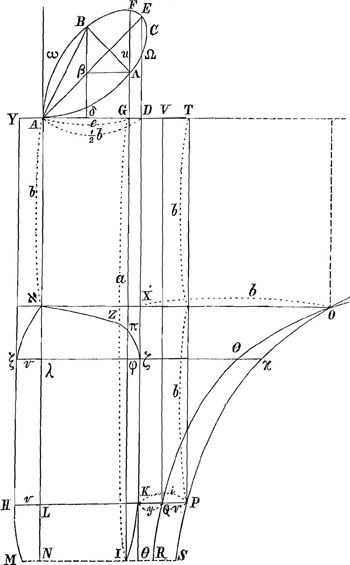³⁾.

Fig. 1.

2) Quadrature de la boucle entière.

3) Voir les notes 21 et 22 de la Lettre N^o. 2777.

[p. 375]

Haberem quadraturam si cognoscerem summam omnium u seu FG in spatio ABED, nam ablato triangulo EAD fiet ABE hoc est ½ spatium folij ABCA.

Sit bbu=aee; unde a=bbu/ee et hinc alia curva construatur KI; cujus aequatio, ex priori data, erit b⁵a-b⁶/a³=e³.

Si haberem aee, haberem et bbu, et hinc u. Sed aee est ⅓ e³. Ergo opus habeo e³ in nova curva.

Sit e³=bbv vel bbi-bby.

bbi=b⁵a/a³; aai=b³; Hyperboloides quadrabilis OPS; cujus spatium infin. KPSθ=▭PD; bby=b⁶/a³; a³y=b⁴; Hyperboloides quadrabilis OQR; cujus spat. infin. KQRθ=½▭QD.

Si tentassem⁴⁾ quadrare portionem ut AΛG, tunc omnes a ad AD applic. terminatae fuissent in curva quadam אZζ, cui convenit ut aee sit ⅓[]E³-⅓e³⁵⁾, hoc est omnes a (Gπ) in quadrata distantiarum suarum ab Aλ, hoc est omnes Gφ minus omnibus πφ in quadrata distantiarum istarum. Sed omnibus πφ in quadrata ista=⅓ cuborum ex e, quae in spatio אζλ......Sed haec via impeditur⁶⁾.

Sumpsi igitur quadrandum spatium ABED, ex quo inventae lineae GI, sive a,

4) C'est ici que commencent les recherches originales de Huygens; ce qui précède pouvant être considéré essentiellement comme un exposé sous une forme plus géométrique et en ordre inverti des indications données par Fermat comme devant mener à la quadrature du folium. Consultez encore la note 14 de la Lettre N^o. 2777.

5) Voir le § IV de la pièce N^o. 2781.

6) Ces mots sont précédés de quelques phrases biffées et illisibles. Remarquons d'ailleurs que le point ζ correspond au point Ω et non au point E. En prolongeant la courbe אζ elle attein drait le point K pour y rejoindre la ligne KI qui appartient à la même courbe.

[p. 376]

constituunt (quod mirum videri queat) spatium DKINA, in quo applicantur e ad rectam AN infinite protensam, fit vero DK=2b⁷⁾, sed curva KI incipere censenda ab infinitâ distantia prope asymptoton NA. In eo vero jam spatio omnes e aequantur omnibus a et omnes eea=⅓ omnium e³⁸⁾.

Porro ex e inveniuntur v, ipsis e indirectum adjunctae⁹⁾; deinde summa omnium v invenitur, in qua computantur primo omnes v in ▭ YALH; deinde omnes MN; incipiendo ab LH, quia KD est prima ac minima omnium a; atque istae MN seu v aequantur porro singulae rectis RS, inter hyperboloides OPS, OQR interceptis ac sibi respondentibus. Incipiunt autem hyperboloides a puncto O, angulo quadrati cujus latus b. Estque spatium infinitum inter eos interceptum PQRS=spatio infinito HLNM. Pro omnibus v igitur habemus omnes quae sunt in ▭ AH et in spatio infinito QPSR, quod aequale invenitur ▭^oTK-▭QX¹⁰⁾; sed quia [] bbv est=[]e³, hoc est [] 3aee, hoc est [] 3bbu, erunt omnia bbv=ter omnibus bbu et ⅓ omnium bbv=omnia bbu. Ergo ⅓ omnium v=omnibus u, quae facere inteliguntur spatium ABED, ductae nempe in unam aequalium partium in quas ipsae u dividunt rectam AD, sicut omnes in infinitum v in aequalem priori particulam ductae in quas v vel e dividunt rectam infinitam ALN, faciunt spatium infinitum AYHMNA, hoc est ▭ KT-▭ QX una cum ▭ AH. Itaque horum tertia pars hoc est ▭ VX¹¹⁾+⅓ ▭ AH sive VK, hoc est ⅚▭ VK aequabuntur spatio ABED.

7) Puisque K est le point de la courbe KI ou e³=b⁵a^-2-b⁶a^-3, pour lequel e=AD=½b.

8) En notation moderne ∫e²a de=⅓∫e³da, en valeur absolue, où toutefois la seconde intégration doit être étendue aussi bien sur la droite KD que sur la courbe IK, ce qu'on ne devra pas perdre de vue dans ce qui va suivre. La relation est correcte puisque ici ae³ s'approche de zéro pour e=o, a=∞.

9) Puisqu'on a v=MN=e³b^-2, où e représente l'abscisse AG du point correspondant I de la courbe KI. Ainsi, pour e=LK=½b, on trouve v=HL=⅓b.

10) Puisque ▭ QX=½▭ QD.

11) On a en effet, pour KD=2b, DV=y=b⁴a^-3=⅛b, DT=i=b³ā²=¼b; donc, puisque DX=½DK, b▭VX=⅛b², ▭KT-▭QX=½b²-⅛b²=⅜b²=3▭VX.

[p. 377]

Sed ▭ VK=¼bb. Ergo spat. ABED=5/24bb, et demto triangulo ADE==⅛ sive 3/24bb, fit sp. ABE=2/24 sive 1/12bb.

Folium ABEΛA aequale ⅓ quadrati ab AE diametro¹²⁾.

12) Huygens ajoute encore sur la figure présente: ‘Spat. אξλ=θΟϰ; ⅓ ▭ Yλ-⅓ spat. אξλ=spat. ADΩ’.

§ II¹³⁾.

Quaeritur quadratura universalis curvae pag. praecedentis.

KP=e⁴/buu¹⁴⁾; DK=a=bbu/ee; spat. infin. KPSθ=[▭ PD]=bee/u.

KQ=e⁶/bbu³; DK=a=bbu/ee; spat. infin. KQRθ=[½▭ QD]=e⁴/2uu.

AY=[v]=e³/bb; DK=a=bbu/ee; ▭ AH=eu.

spat. A [ω] Bδ=bee/3u-e^4/6uu+eu/3^15).

spat. B [ω] Aβ, si Aδ sit e, δB=u, =spat. A [ω] Bδ-ΔAβδ=bee/3u-e⁴/6uu+

+eu/3-½ee.

spat. AβB [ω]+AβΛ=2 spat: B [ω] Aβ=2bee/3u-e⁴/3uu+2eu/3-ee.

spat. A [ω] BΛA=spat. AβB [ω]+AβΛ+triang. BβΛ=2bee/3u-e⁴/3uu++2eu/3-ee+½uu-eu+½ee=⅔bee/u-⅓e⁴/uu+½uu-⅓eu-½ee; quadratura universalis.

13) Quadrature du segment AωB de la fig. 1.

14) On doit considérer dans ce qui va suivre le point E comme un point indéfini de la courbe ABE. Alors KP=i=b³a^-2, où a=bbue^-2; donc KP=e⁴b^-1 u^-2.

15) En effet, la relation spat. ABED=⅓spat. infinit. KPSθ-⅓ spat. inf. KQRθ+⅓□ AH, qui se déduit facilement des données du paragraphe précédent, est encore valable pour un point quelconque B de la courbe ABE. D'ailleurs Huygens ajoute ici en marge: ‘In his e et u sumuntur pro maximis linearum e et u quae pag. praecedenti in calculo adhibentur; quae nimirum maximae portionem quamque datam definiunt’.

[p. 378]

(Si u=e:⅔be-⅓ee-⅓ee, fit e=½b, ⅓bb-⅙bb=⅙bb, sicut pag. praec. inveneram).

bue-e³=u³; buee-e⁴=eu³; bee/u-e⁴/uu=eu;-⅓e⁴/uu=⅓eu-⅓bee/u spat. A [ω] BΛA=⅓bee/u+½uu-½ee; quadratura universalis brevior.

NB. Hic perpend. u, esse eam quae a superiori ambitu folij ducitur.

Spat. A [ω] Bδ=bee/3u-e⁴/6uu+eu/3; si hic restituatur valor-e/6uu fit spat. A [ω]B δ=⅙bee/u+½eu. Triangulum ABδ=½eu. Spat. AωBA=⅙bee/u; segmentum.

§ III¹⁶⁾.

Quaeritur spatium A[π] fD [fig. 2], cum Af est continuata curva EωA pag.^ae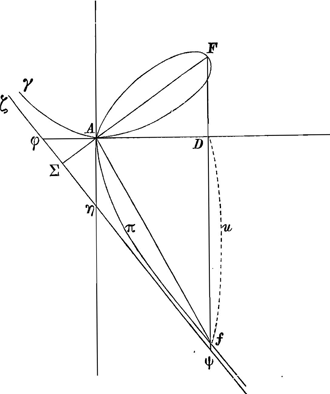

Fig. 2.

16) Quadrature du segment Aπf et de l'espace infini γ Aπf ψ Σζ.

[p. 379]

141¹⁷⁾. Proprietas hujus Af est ut differentia cuborum AD, Df sit aequalis solido ex AD, Df et data b.

AD=e; Df=u; u³-eub-e³=o¹⁸⁾; u³-eub=e³; bbu=aee; a³e³-ab⁵==b⁶; e³=b⁶+ab⁵/a³; e³=bbv=bbi+bby; bbi+bby=b⁶/a³+b⁵/aa

i+y=b^4/a^3+b^3/aa; i=b^3/aa; aai=b^3; y=b^4/a^3; a^3y=b^4.

Omnia erunt eadem ac pag. 142¹⁹⁾ praeter unum signum quod hic in+mutandum.

Ergo spat. A[π]fD=bee/3u+e⁴/6uu+eu/3; restitue valorem e⁴/6uu, hic=eu/6--eeb/6u²⁰⁾; spat. A[π] fD=⅙bee/u+½eu; ½eu=triang. ADf; spat. AπfA==⅙bee/u; AΣ=⅓b, nam AΣ=⅓ AE²¹⁾, φD=⅓b+e; ΔφDψ=1/18bb++⅓be+½ee; ΔφAη=1/18bb; sp. AηψD=ΔφDψ-ΔφAη=⅓be+½ee.

sp. Aηψf finitum=sp. AηψD-sp. A[π]fD=⅓be+½ee-⅙bee/u-½eu; e+⅓b=u, cum e infinit.; ½eu=½ee+⅙eb; sp. Aηψf infinitum (restituto valore -½eu)=⅙eb-⅙bee/u=⅙eb-⅙bee/e+⅓b; hic uterque terminus infinitum efficit spatium extensione, ex quibus disferentia colligi nequit, neque putandi sunt aequales eo quod e+⅓b in divisore facit idem quod e ut videri posset. Patet enim differentiam eorum esse 1/18ebb/e+⅓b. Sed divisor e+⅓b, cum e infinitum, idem valet

17) Voir la figure 1 de cette pièce.

18) Cette équation est déduite de celle du § I par le changement du signe de la variable u.

19) Voir le § II de la présente pièce.

20) Elle est obtenue au moyen de l'équation u³-eub-e³=0.

21) Lisez plutôt AF. La relation est indiquée aussi dans la Lettre N^o. 2777, mais nous n'en avons pas rencontré la déduction dans le manuscrit de Huygens. On a de plus: AD=½b, d'où la valeur de Aϕ se déduit facilement.

[p. 380]

quod e solum, in hac determinata quantitate plani. Ergo 1/18bb=spatium infinitum Aηψf; 1/36bb=triang. AΣη; 1/12bb spat. infin. AΣψf; ⅙bb spat. infin. γAfψΣζγ aequale folio ABEΛA [fig. 1], quod erat ⅙bb.