|
| |
| |
| |
No 2833.
Christiaan Huygens au Marquis de l'Hospital.
5 novembre 1693.
La minute se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. UylenbroekGa naar voetnoot1).
La lettre est la réponse au No. 2830.
De l'Hospital y répondit par le No. 2838.
Huygens au Marquis de l'Hospital.
5 Nov. 1693.
Devant que de respondre à celle que je viens de recevoir de vostre part, je suppleeray icy ce que je devois dire sur 2 articles de votre precedente Ga naar voetnoot2). L'un estoit touchant la necessitè d'une seconde series pour les quadratures, outre celle que vous avez commune avec Mr. Gregori, laquelle equivalence je n'ay pas encore assez examinée. J'avois donc dit que je ne vois pas la necessitè de cette seconde series, dont vous jugerez apres avoir considerè ce qui s'ensuit. Vous scavez, Mr. sans doute la maniere de trouver l'equation d'une courbe lors que sa quadrature est donnée Ga naar voetnoot3). Par exemple quand l'aire d'une courbe est a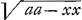 , x estant l'abscisse, a une ligne donnée Ga naar voetnoot4). On en trouve l'equation aaxx ∞ aayy- xxyy, où
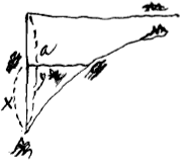
Fig. 1.
y est l'appliquée Ga naar voetnoot5). De mesme quand l'aire est donnée aa- a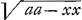 , l'on trouve la mesme equation de courbe aaxx ∞ aayy- xxyy. Donc si cette equation de courbe est donnée, je trouveray par la seule premiere suite de Mr. Gregori, son aire a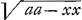 , sans avoir besoin de la seconde suite qui avec la premiere feroit trouver l'aire aa- a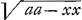 . Il y a seulement à remarquer que l'aire a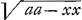 sera l'espace infini des appliquées sur a- x, et que l'aire aa- a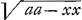 sera l'espace des appliquees sur x,
| |
| |
mais cette derniere se peut encore trouver sans considerer la 2.de suite, parce qu'on voit qu'en posant dans la premiere x ∞ 0, l'aire devient ∞ aa, qui est quantité connue qui resulteroit de la 2.de suite. Et cela arrive tousjours ainsi.
Le second article estoit la description des courbes de Mr. Jo. Bernoulli. Je me sers pour la faire de cordes et de rouleaux. Ainsi si on veut decrire la courbe AC [Fig. 2] dont les tangentes CD soi[en]t double[s] des abscisses DA, il faut que la corde DBEFBDC soit enveloppée sur le rouleau EF tournant sur son centre fixe, alors en menant le stile D, où elle est attachée, le long de la regle BA, de D
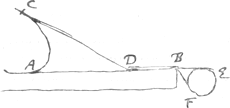
Fig. 2.
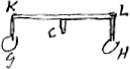
Fig. 3.
vers A, elle attirera la pointe C, qui decrira la courbe requise CA; laquelle pointe on peut tenir perpendiculaire sur le plan horizontal par cette invention d'equilibre, [Fig. 3] ou les 2 poids egaux G, H, sont attachez à la double equerre GKLH et pendent plus bas aux costez du plan horizontal que n'est la pointe C.
Dans ce cas la description est la plus simple. Dans les autres quand la tangente est plus grande que l'abscisse, il faut un double rouleau ou bien deux rouleaux attachez l'un sur l'autre, et qui tournent ensemble sur un mesme axe, comme dans cette autre figure, et il faut que le sil attaché au stile D aille envelopper le rouleau
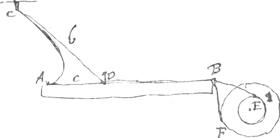
Fig. 4.
E, et qu'un autre sil, qui enveloppe le rouleau F du sens contraire passe par BDC, qui attirera la pointe C pendant qu'on mene le stile D vers A. Et si l'on veut que la raison de la tangente à l'abscisse soit comme b à c, il faut que le diametre du rouleau F qui tire soit au diametre de l'autre E, qui est tiré, comme b- c à c. Ainsi, si CD doit estre triple de AD, le rouleau F doit avoir le diametre double du rouleau E.
Lors que la tangente doit estre moindre que l'abscisse, c'est-à-dire b moindre que c, il y a un peu plus de façon, par ce qu'il faut tracer à part les deux parties CA terminée et CQ infinie [Fig. 5]. Pour descrire CA il faut que la corde qui vient du stile D, auquel elle est attachée, enveloppe le rouleau E, et qu'une autre corde enveloppe du mesme sens l'autre rouleau F, et qu'elle aille par BDC, et tire la pointe C pendant qu'on menera le stile D vers A. Et la proportion du diametre
| |
| |
de E à celui de F doit estre comme c à c- b. Mais pour la partie CQ, il faut placer le rouleau composé de l'autre costé de A, et faire que la corde qui vient du
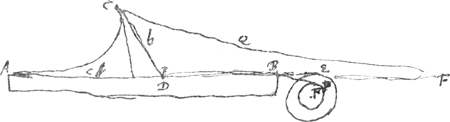
Fig. 5.
stile D enveloppe le moindre rouleau F; et que l'autre corde qui du mesme sens enveloppe le rouleau E, aille par BDC pour tirer la pointe C, pendant qu'on éloigne le stile D de A. Mais il faut pour cela qu'on empesche le mouvement aisé
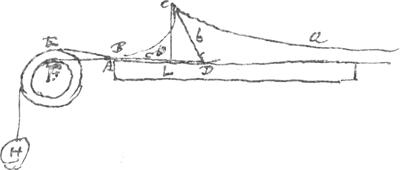
Fig. 6.
des rouleaux comme par un poids H, autrement la corde EDC se relacheroit Ga naar voetnoot6).
| |
| |
La raison des diametres de E et F doit estre icy comme b+c à c, de sorte qu'elle est autre que pour la partie CA et le mesme rouleau composé ne scauroit servir. Si on veut que la tangente CD fasse la moitiè de l'abcisse, les diametres des rouleaux pour AC seront comme 2 à 1, mais pour CQ ils seront comme 3 a 2. Vous trouverez bien aisement les raisons de tout cecy par un petit calcul. Je ne me suis arrestè que trop longtemps a ces petites speculations. J'adjouteray seulement que le point C, où commencent les parties CA, CQ est celuy du quel estant menè la tangente CD, et la perp. CL a l'asymptote, la raison de CD a DL est comme de c à b, ce qui se peut aussi montrer aisement par le calculGa naar voetnoot7), et je l'avois remarquè sans cette aide et devant que d'avoir resolu le problemeGa naar voetnoot8). On peut par la maniere de Mr. Bernouilli descrire toute la partie CA, parce que le fil CD va en s'accourcissant mais rien de l'autre CQGa naar voetnoot9), parce que ce fil devroit s'allonger.
| |
| |
Je viens, Mons.r, à vostre lettreGa naar voetnoot10), où je vois que vous avez fort bien demeslè l'origine de la construction des caustiques qui est dans les Acta; mais ces lignes a peine meritent elles que vous prissiez cette peine, quel que beautè ou utilitè qu'y veuillent trouver Mons. TchirnhausGa naar voetnoot11) et Ja. Bernoulli.
Mr. l'Abbé Catelan n'a donc pas mieux reussi dans sa science generale des lignes courbes que dans sa critique, qu'il publia cy-devantGa naar voetnoot12) contre ma Theorie du centre d'agitation. Il faut avouer que la geometrie n'est pas faite pour toute sorte d'esprits.
J'avois promis de vous dire mon sentiment touchant le livre de la manoeuvre des vaisseauxGa naar voetnoot13). Vous allez l'apprendre par l'imprimè cy-jointGa naar voetnoot14), qui est une feuille de nos Journaux. Celui, qui les compose, m'aiant prestè ce livre, m'avoit priè de luy donner par ecrit cette Remarque et j'ay bien voulu qu'elle fust publique puis qu'il importoit de refuter une fausse Theorie qu'on propose pour instruire les Pilotes. Je m'estonne que tant de personnes scavantes l'aient pu trouver bonneGa naar voetnoot15).
Il y avoit quelques points dans mes lettres precedentes aux quels j'avois souhaitè vostre reponse, mais ce sera à vostre loisir. Pour à cette heure je demande seulement qu'il vous plaise de me faire response au plus tost sur ce que je vais vous demander touchant la recherche de Mr. Jo. Bernoulli, sur la figure de la voile, car vous m'avez fait scavoir que vous aviez conferè la dessus avec luy. Je voudrois donc scavoir s'il pretend qu'une voile faite de parallelogrammes egaux et inflexibles (que je represente icy par des lignes droites) A, B, C, D, E, F, G, H
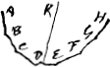
estant etendue par le vent se tiendrait courbée, de mesme que feroit une telle chaine par son poids, puisqu'il assume que la chaine et la voile font la mesme courbure. Il me semble qu'il doit affirmer cela, parce qu'il me semble impossible autrement de rien penetrer dans cette affaire. Cependant je puis demon- | |
| |
trer que cela n'est pas ainsiGa naar voetnoot16). Le Professeur a avancé de grandes absurditez touchant cette tension de la voileGa naar voetnoot17), lesquelles j'ay envie de refuter en mesme temps. Je suis avec respect, etc. |
-
voetnoot1)
- Chr. Hugenii etc. Exercitationes Mathematicae, Fasc. I, p. 301.
-
voetnoot3)
- Voir, sur la méthode suivie à cet effet par Huygens, le § I de la pièce No. 2736.
-
voetnoot4)
- Voir la figure 1. A cause des renvois de la Lettre No. 2819, note 21, et de la Lettre No. 2828, note 14, nous avons numéroté les figures.
-
voetnoot5)
- Consultez, sur la quadrature de cette courbe et sur la manière de la retrouver en partant de la quadrature, le § II de la pièce No. 2669 et les Lettres No. 2672 et 2673. Ajoutons qu'elle est représentée par la figure 1, dessinée par Huygens en marge de la minute, comme on le reconnaît en comparant cette figure avec celle de la Lettre No. 2672.
-
voetnoot6)
- Il y a ici une méprise, puisque c'est en réalité la corde FD qui se relâcherait, si la pointe C restait en place, faute d'une tension suffisante de la corde EDC. Pour s'en convaincre, un petit calcul suffira. Supposons à cet effet que le style D soit déplacé vers la droite sur la petite distance Δ. Alors, si la pointe C reste en place, la corde CD s'allongera de la quantité Δ. cos CDB et par suite une longueur de corde Δ (1+cosCDB) se déroulera du rouleau E. En conséquence, le rouleau F laissera échapper la longueur c/b+c Δ (1+cos CDB) et le fil FD devra se relâcher aussitôt qu'on aura c/b+c Δ (1+cosCDB) > Δ, c'est-à-dire, cos CDB > > b/c; mais c'est là précisément ce qui a lieu, comme on le verra dans la suite, pour toute la partie CQ de la courbe.
Si, au contraire, le poids H entrave suffisamment le mouvement du rouleau, la corde FD restera tendue, le rouleau E délivrera la longueur de corde b+c/cΔ, dont la portion b+c/cΔ-Δ=b/cΔ servira à allonger le fil CD, et la pointe C, au lieu de rester en place, devra s'avancer vers la direction CD par la distance (cos CDB - b/c)Δ.
Ajoutons que l'on rencontre la même méprise dans la remarque de Huygens citée dans la note 14 de la Lettre No. 2828.
-
voetnoot8)
- On peut consulter, quant aux premières recherches de Huygens sur le problème de Bernoulli, la note 17 de la Lettre No. 2819. Sans doute Huygens aura dû rencontrer le point de rebroussement à la même occasion qu'il découvrit la nécessité d'employer deux arrangements divers pour les portions CA et CQ de la courbe. En effet, à la même pag. 49 du livre J mentionné déjà dans la note citée, on rencontre l'annotation suivante, qui se rapporte à la détermination du point C comme point limite de la portion de la courbe, dont la description est possible au moyen de l'arrangement de la figure 6. Adaptant les notations à celles de cette figure, l'annotation se lit comme il suit: ‘Pour tracer CQ infin. Filum affixum stylo in
D incedens per DBF trahit orbiculum F. Simulque orbiculum E remittit filum alterum EBDC, quod per foramen stili mobilis D transit, et affigitur stylo describenti C. Quod si velim ut curva CQ sit ejusmodi ut semper tangens CD sit ∞ ½ abscissae DA, debet orbiculus E habere diametrum sesquialterum diametri orbiculi F. Sed hoc modo tantum pars curvae CQ infinita describitur, quam Bernoullii machinula non potest describere. Incipit autem haec pars a puncto C cujus tangens CD abscindit DL inter ipsam et perpendiculum CL, ita ut CD ad DL sit dupla, in hac quidem curva; in omnibus vero ut CD ad DL habent rationem abscissarum ad tangentes’.
-
voetnoot11)
- Voir les articles mentionnés dans la note 4 de la Lettre No. 2274 et dans la note 15 de la pièce No. 2626.
-
voetnoot12)
- Voyez la pièce No. 2260 et consultez, pour la polémique qui s'ensuivit, les Tables des Matières des Volumes VIII et IX et du volume présent sous l'article ‘Polémique avec l'abbé de Catelan’.
-
voetnoot15)
- Probablement Huygens fait allusion aux critiques très favorables qui avaient paru dans le ‘Journal des Sçavans’ du 12 décembre 1689 et dans les ‘Acta eruditorum’ d'août 1690. De plus, dans l'article mentionné dans la note 25 de la Lettre No. 2819, Jacques Bernoulli avait cité la fin du traité de Renau dans les termes: ‘sub finem libelli egregii’, à propos de quoi Huygens avait annoté en marge de l'article: ‘sed pleni paralogismis’.
Comparez encore la lettre de Huygens à Fatio de Duillier, du 30 novembre 1693.
-
voetnoot16)
- Consultez, sur cette démonstration, l'Appendice II à la présente lettre, la pièce No. 2835.
-
voetnoot17)
- En consultant les ‘Notes marginales’ (voir la note 1 de la pièce No. 2540) sur les articles de Jacques Bernoulli, citées dans la note 32 de la Lettre No. 2693 et la note 25 de la Lettre No. 2819, on s'aperçoit qu'il s'agit des points suivants: 1o. de l'assertion mentionnée dans la note 33 de la pièce No. 2693 et répétée dans le second des articles cités, d'après laquelle une partie de la voile se courberait en arc de cercle, 2o. de celle, dont Huygens croyait avoir prouvé l'inexactitude, d'après laquelle l'autre portion de la voilière serait identique avec la chaînette, 3o. de l'importance exagérée attachée par Jacques Bernoulli à la connaissance de la forme exacte de la voile au point de vue nautique, ce qui l'avait séduit à écrire: ‘adeo ut totius negotii certitudo tandem in cognitione Figurae veli terminetur,
quae quia hucusque latuit, efficit, ut Nautae nondum optatum in his finem assequi potuerint, & fallacibus plerumque conjecturis deludantur’ (‘Nugae!’ annota Huygens), attribuant même à l'erreur de traiter la voile comme une surface plane un ‘damnum inaestimabile hominum merciumque’, et ajoutant plus loin: ‘Ego interea pro homine mediterraneo ad negotium maritimum, quo non est aliud e quo rebus humanis major accedit utilitas, plus satis contulisse mihi videor’, a propos de quoi Huygens remarque: ‘Imo haec nullius usus essent, etiamsi vera’; 4o. du théorème suivant: ‘Celeritas navium eodem secundo vento velitantium, caeteris paribus, sunt ut velorum subtensae’, sur lequel Huygens annota: ‘Errat, imo sunt in ratione subdupla velorum subtensorum. Ita enim fiunt resistentiae sicut vires impellentes’.
A propos de cette dernière remarque nous ajoutons encore qu'on trouve dans le même article de Jacques Bernoulli la phrase: ‘Vis, qua Velum....impellitur, componitur ex celeritate venti, et subtensa veli’, d'où il s'ensuit que l'auteur y considera en effet la pression du vent sur la voile & la résistance de l'eau contre la proüe comme variant dans la raison simple de la vitesse, ce qui est assez étrange, puisque les mêmes principes qui doivent l'avoir guidé, lui et son frère, dans leurs recherches sur la courbe de la voile (voir sur ces principes la Lettre No. 2838), conduisent à la raison double. Aussi, dans l'article mentionné dans la note 22 de la Lettre No. 2818, a-t-il rétracté le théorème en question, prétendant qu'il avait eu en vue les vitesses ‘initiales’; les vitesses stationnaires étant ‘ut Radices subtensarum veli’.
|





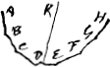


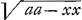 , x estant l'abscisse, a une ligne donnée
, x estant l'abscisse, a une ligne donnée