Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 534]

N^o 2828.
Christiaan Huygens au Marquis de l'Hospital.
1^er octobre 1693.

La minute se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek¹⁾.
La lettre est la réponse au No. 2825.
De l'Hospital y répondit par le No. 2830.

Sommaire.²⁾
Sa solution est a admirer a cause du chemin difficile. Bernouli se trompe en la condamnant comme fausse. puto posse reduci ipsius constructionem ad meam seu Bernoulianam. apparet quando futura sit geometrica curva nempe quando p-q vel q-p ad q ut numerus ad numerum: per logarithm. possunt aequalia trapezia hyp. abscindi. Una tantum datur curva quae satisfaciat, non duae ut putat. Fit enim aequatio ejus prima eadem quae Bernoulij, si ponatur 108 b, pro a, et dividatur per 432. ma construction. qualis curvae integrae. quomodo in circumferentiam abeunt. et in rectam. ma machine pour la description. Flexilis ambitum³⁾. an habet quadraturam lineae y=aax/aa+xx ex quadratura hyperbolae⁴⁾?

A la Haye ce 1 Oct. 1693.

J'ay esté etonnè, Monsieur, de voir que par le chemin que vous avez pris on pouvoit aussi parvenir à la solution du Probleme de Mr. Bernouili, et j'ay admirè vos excellents artifices, qu'il y a falu emploier, où il y a bien des choses, qui peuvent servir en d'autres occasions, et sur les quelles j'auray à vous consulter cy-apres quand j'auray le loisir de les examiner a fonds. Mr. Bernouilli se trompe assurement, quand il soutient que vostre solution n'est pas bonne, estant certain, que toutes vos deux equations s'accordent avec la siene⁵⁾. Je dis toutes les deux, par ce que si dans la 1^re, l'on suppose 108 b ∞ a, et qu'on divise apres par 432, on

1) Chr. Hugenii etc. Exercitationes Mathematicae, Fasc. I, pag. 296.

2) Ce sommaire est emprunté à la page 63 du Livre J.

3) Comparez l'anagramme de la fin de la pièce N^o. 2823 et la fin de la présente pièce.

4) Nous n'avons pas trouvé cette quadrature dans les manuscrits de Huygens. On remarquera que la question n'a pas été traitée dans la lettre.

5) En outre Huygens s'était assuré, à la page 62 du Livre J, de l'identité des solutions de Bernoulli et de l'Hospital avec celle de Jacques Bernoulli pour le cas particulier p=2q. Posant, dans la figure 3 de la pièce N^o. 2821, AD=x, CD=y. CG=z, on trouve facilement (appliquant la formule de l'avant-dernière ligne du § IV de la même pièce où l'on doit remplacer 2x par z et où z représente, après changement de signe, la ligne DG) DG=(az-z²)∷(a+z), donc x=(az-z²):(a+z)+½z, ou bien z²=3az-2ax-2xz.
D'un autre côté on a z²-y²=GD²=(x-½z)², donc z²=-4/3 xz+4/3 x²+4/3y². En égalant ces deux expressions pour z², Huygens trouve aisément z=(6ax+4x²+4y²)∷(9a-2x); après quoi la substitution dans la seconde expression pour z² amène l'équation cherchée: 4y⁴+4x²y²-27a²y²+36axy²+32ax³=0, qui devient identique avec celle de Bernoulli en supposant a=2b. Remarquons que les deux constantes a et b ont chacune une signification géométrique très simple; celle de Huygens représentant la ligne BO de la figure mentionnée et celle de Bernoulli la ligne AO de la même figure.

[p. 535]

trouve justement son equation. Ce que je m'estonne que vous n'aiez pas remarquè, Mons^r., en luy faisant response, aussi bien que vous l'aviez decouvert dans la seconde. Il n'y a donc pas deux differentes courbes qui satisfassent au Probleme, comme vous aviez cru, mais vos deux constructions donnent la mesme, quoy que de differentes grandeurs. Je crois mesme qu'on les pourroit reduire à la mesme simplicité de la miene que vous verrez icy, qui resulte aussi de la solution de Jac. Bernouilli que vous avez vue dans les Acta du mois de Juin. Car pour ce qui est des trapezes Hyperboliques égaux que vostre construction demande qu'on puisse retrancher, cela se fait aisement par le moien de la Logarithmique, et pour venir à ma construction, il a falu y passer de mesme, comme vous pouvez juger par ce que je vous ay ecrit dans ma precedente. Cette construction donc⁶⁾ est comme s'ensuit.

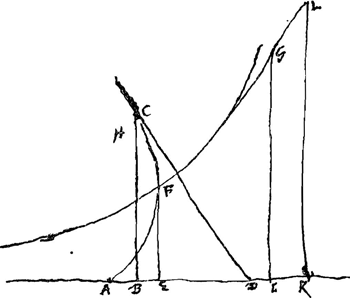
Soit donné dans la droite AB, le point A, et qu'il faille trouver la courbe AFC telle que quelque droite qui la touche, comme CD, retranche dans AB la partie AD, qui ait à CD une raison donnée.

Constr. Supposant la Logarithmique quelconque FG, aiant l'asymptote AB, de quelque point qu'on y aura pris, soit appliquée la perpendiculaire FE. Et comme b à c ainsi soit FE à

6) Huygens l'a publiée plus tard dans l'article cité dans la note 11 de la Lettre N^o. 2823.
Elle a été déduite probablement à l'aide de la proportion qui se trouve dans le § VII de la pièce N^o. 2821, et où l'on a, l'unité étant représentée par EF, θ=b:c; x=AD:EF; θx=CD EF; z=BD:EF.

[p. 536]

EA⁷⁾. Puis aiant pris vers E quelque distance AD, et faisant comme c à b ou AE à EF, ainsi AD à une autre DC, on decrira avec celle-cy comme raion et du centre D, la circonference CH, et l'on appliquera IG egale à la mesme DC. Puis comme b à deux fois c, ainsi on fera IE à EK, qu'on prendra vers l⁸⁾, et on appliquera derechef à la logar.^que la perpend. KL⁹⁾; et comme la somme des lignes KL, EF à leur difference, ainsi on fera DC à DB, qu'il faut prendre vers le point A, si AD est plus grande que AE, ou du costè opposè si elle est moindre. Maintenant la droite BC perpend. à l'asymptote, coupera la circonf. CH, au point C, qui sera dans la courbe cherchée AFC.

Je crois que vous aurez remarqué que lors que c est plus grande que b, la Ligne n'a pas une courbure simple, mais deux différentes, qui aboutissent à un mesme



point, comme ANM, MP¹⁰⁾, laquelle derniere a l'asymptote AQ, la mesme que la Logarithmique. Lorsque ANM devient une demie circonf., il semble que cette MP devient une ligne droite et vous trouverez, comme je crois, que c'est celle que donne vostre construction dans le cas que b et c sont egales.

Le chemin abregè que vous avez rencontrè apres avoir escrit vostre lettre est celuy que j'ay suivi, et sans doute aussi Mr. Bernoully, mais j'ay au/n-nuu=-dz/z¹¹⁾, par ce que n est plus grand que nuu. Et pour ce signe

7) De cette manière F représentera le point de la courbe cherchée, pour lequel la tangente FE se trouve perpendiculaire à l'axe AD.

8) Comme cela résulte de l'article mentionné dans la note 6, Huygens a vu plus tard qu'on pouvait prendre EK tout aussi bien vers l'autre côté.

9) On a donc par construction: l(KL:EF)=EK/El l (IG:EF)=2/θ l (CD:EF)=2/θ l (θx) et ainsi: KL=(θx)^2/θ EF.

10) Consultez, sur le point de rebroussement M, dont l'existence avait échappé à de l'Hospital et probablement aussi aux Bernoulli, la Lettre N^o. 2833 à de l'Hospital du 5 novembre 1693

11) Comme on le voit, cette formule est identique, même quant au signe, avec celle indiquée par de l'Hospital. Pour la déduire de ses propres calculs, Huygens a pu partir de la formule dont il est question dans la note 18 de la pièce N^o.2821, c'est-à-dire de celle qui ouvre le § V de cette pièce, après changement toutefois du signe du second membre. Ensuite, pour se conformer à la notation de de l'Hospital, il a dû remplacer a par l'unité, θ par n^-1, x par nz, n=az: x par x:nz=n^-1 n; an par n^-1 du; ce qui amène en effet la formule du texte.

[p. 537]

de - devant dz/z, il ne doit point faire de peine, qui seroit+dans les cas que la



touchante CD est inclinée de l'autre sens que dans vostre figure¹²⁾, c'est-à-dire dans celle-cy.

J'avois dessein de vous envoyer la maniere que j'avois imaginee pour descrire mechaniquement ces courbes¹³⁾, mais je vois qu'il y a à considerer quelque chose de plus dans les cas que c est plus grande que b¹⁴⁾, et je n'ay pas maintenant assez de temps

12) Ce changement de signe, inévitable dans les formules de Huygens (voir la pièce N^o. 2821 et la figure 3 de cette pièce) où le z représente toujours la valeur absolue de la soutangente GD et n la valeur, toujours positive, du quotient: az:x=BO×z:AG, est déplacé dans celles de de l'Hospital.

13) Dans la minute de la présente Lettre Huygens avait même achevé cette description pour le cas c < b. Quoique identique en principe avec celle que l'on rencontrera, pour le même cas, dans la Lettre à de l'Hospital N^o. 2833, elle est plus détaillée et un peu différente quant au choix des moyens d'exécution. Nous croyons donc faire bien de la reproduire ici, telle qu'on la trouve dans le passage en question, biffé par Huygens:
‘Ma maniere de decrire cette courbe est telle. Sur une table exactement horizontale soit fixée la regle BE, contre laquelle glissera une autre regle HG. Proche du bout de la regle EB



il y a deux rouleaux O, M, attachez ensemble et mobiles sur l'axe L fichè dans la table, ayant leurs diametres en la raison de c à b-c. D est un petit oeil attachè au costè de la regle mobile, et K un autre oeil fichez dans la table, en sorte que le fil DK qui passe par la deux soit couchè le long de la dite regle. Ce fil est attachè a la pointe C qui doit decrire la courbe et passant en CDK, est enveloppè et attachè sur la circonference du rouleau M; et un autre fil EO est attachè en Q au bout de la regle mobile, qui va glissant contre la regle fixe, mais ce fil passe aussi par un petit oeil fixé sur la table en P, vis à vis de K. Si on avance maintenant la regle HG vers B, le fil QO fera tourner ensemble les rouleaux O, M, et la regle mobile GH et l'oeil D, avanceront la moitié aussi viste vers A que la pointe C’, c'est-à-dire dans le cas où b=2c, lorsque les deux rouleaux, ayant le même diamètre, peuvent être remplacés par un seul, comme dans la figure 2 de la Lettre N^o. 2833.

14) Quelle peut avoir été la difficulté qui a frappé Huygens pendant la rédaction de la présente lettre? Quand on consulte la page 49 du Livre J, mentionnée dans la note 17 de la Lettre N^o. 2819, on y rencontre déjà des figures moins détaillées mais analogues aux figures 5 et 6 de la Lettre N^o. 2833, qui représentent dans le cas c > b les deux méthodes de décrire la courbe ANMP, dont l'une est valable pour la partie ANM, et l'autre pour la partie MP. Seulement dans la figure 6 le poids H qui entrave le mouvement trop facile des rouleaux manque encore dans la figure correspondante de la page 49 et la remarque ‘ut [ED] tensum maneat oportet ut orbiculi renitantur motui’, qu'on y trouve, semble avoir été ajoutée plus tard. Il est donc probable que Huygens s'est aperçu tout à coup qu'il fallait un nouvel artifice pour empêcher que le fil FD ne se relâchât (car c'est bien ce fil et non ED, comme nous le montrerons dans la note 6 de la Lettre N^o. 2833, qui est sujet à se relâcher) la pointe C restant en place.

[p. 538]

de reste. Je differe donc aussi de vous respondre touchant ce que vous dites des quadratures par les series et touchant le livre de Monsieur Renaud.

J'ay envoié à Mr. Leibnitz une feuille pour estre inserée au Journal de Leipsich¹⁵⁾, où je fais voir seulement que j'ay resolu le Probleme de Mr. Bernoulli sans en dire d'avantage que ce que je vous en marquay dans ma precedente, a fin de laisser de l'exercice à ceux qui s'y voudront occuper. J'y ay aussi parlè de la courbe que je vous dis que j'avois trouvée, et j'ay adjoutè qu'elle sert à regler et rendre egal le mouvement de certains horologes, que j'ay nouvellement inventez, qui est tel que l'agitation de la mer ne scauroit luy nuire ni l'affoiblir, comme il arrive aux pendules, non obstant toutes les precautions. Je suis avec etc.

15) Voir la pièce N^o. 2823.