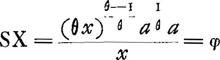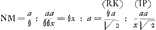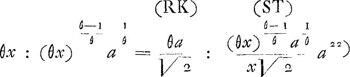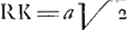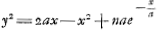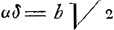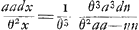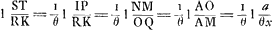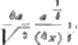|
-
voetnoot1)
- La pièce a été composée entre le 3 et le 10 septembre 1693, dates des Lettres Nos. 2819 et 2820.
-
voetnoot2)
- Cet Appendice contient la solution de Huygens du problème de Bernoulli. Il est emprunté aux pages 52-57 du livre J. Nous l'avons divisé en paragraphes.
-
voetnoot3)
-
Analyse du cas GC=2AG appliquée à la partie inférieure de la courbe cherchée jusqu'au point T où la tangente devient perpendiculaire à l'axe AO.
-
voetnoot4)
- Ici dz=PF-QG représente évidemment le décroissement de z correspondant à l'accroissement dx de x. Ainsi l'équation qui va suivre n'est pas correcte suivant la conception moderne de la notation employée. D'ailleurs, dans la déduction de la formule plus générale, où GC=θx et dont il sera question dans la note 18 de la présente pièce, Huygens a donné à dz la signification usuelle, s'apercevant, comme sa figure, que nous n'avons pas reproduite, le démontre, qu'en prolongeant la courbe OP elle va s'abaisser au point A et qu'ainsi, à partir de ce point A, les z commencent à s'accroître, pour ne décroître que plus loin.
-
voetnoot5)
- Huygens fait suivre encore l'application à cette équation de la substitution xz=n, ce qui amène l'équation simplifiée 4dn=4xdx-n2x-3dx. Ensuite il passe au cas du § II.
-
voetnoot6)
-
Analyse du cas GC=2AG appliquée à la partie de la courbe supérieure au point T.
-
voetnoot7)
- L'équation différentielle de la courbe OQ ayant été obtenue ainsi, il va s'agir, dans ce qui suit, de la simplifier par la substitution az=nx.
-
voetnoot8)
- L'équation différentielle de la courbe OQ est reprise pour y appliquer la substitution mentionnée.
-
voetnoot9)
-
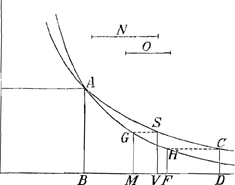
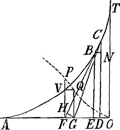
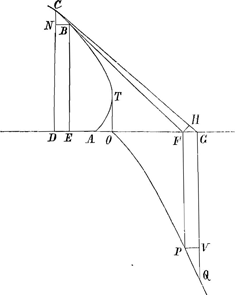
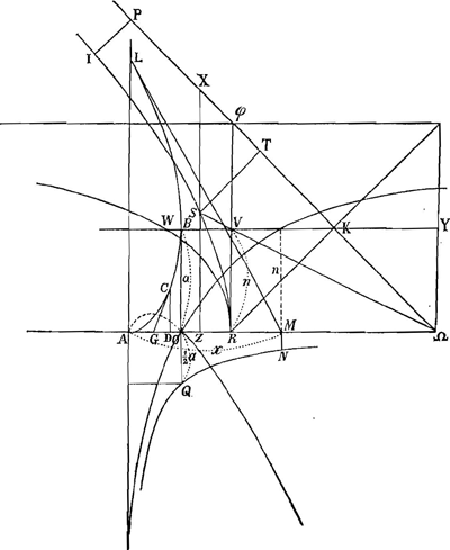
Intégration géométrique de l'équation différentielle du paragraphe précédent. Voici le raisonnement que Huygens nous semble avoir suivi pour arriver aux résultats de ce paragraphe. D'après l'équation différentielle du paragraphe précédent on a:aadx/4x=⅛ 8a3dn/4aa-nn, ou bien (posant 2a=b)=⅛ b3dn/b2-n2; ainsi des deux courbes y=aa/4x (l'hyperbole QN de la figure) et v=b3/b2-n2 (la courbe RW), l'aire de la première doit être égale à la huitième partie de celle de la seconde entre des valeurs correspondantes de x et n. Pour la première couple des valeurs correspondantes, que l'on peut choisir à volonté, Huygens a pris les valeurs x=½a, n=0, qui doivent correspondre, puisqu'on a alors z=0, avec le point B de la courbe ABL pour lequel la soustangente est égale à zéro.
Soient ensuite AM=x et ΩY=RV=n (égale dans la figure à a mais qu'on doit considérer comme variable) deux autres valeurs correspondantes; alors on doit donc avoir:aire QNMO=⅛ aire RWYΩ; mais comme la courbe RW est identique avec la courbe άλλβ de la fig. 1, p. 24, de la pièce No. 2661, dont Huygens avait appris, dans le § III de la pièce citée, à réduire la quadrature à celle de l'hyperbole, cette égalité pouvait se réduire à celle de deux aires hyperboliques. Simplifiant encore un peu le résultat qu'il avait obtenu autrefois, Huygens pouvait poser en conséquence:aire QNMO=⅛RWYΩ=¼RSΩ=¼RSTK=⅛RIPK (pour IP:ST=ST:RK).
Dès ce moment il ne s'agissait plus, pour arriver à la construction cherchée des valeurs correspondantes de x et de n, que de faire en sorte que l'aire RKPI devienne égale à huit fois l'aire OQNM. Or, puisque le carré sur 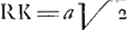 , pour RΩ=b=2a, était justement égal à huit fois le carré sur OQ=½a, il suffisait pour cela de choisir IP de telle sorte que IP:RK=MN:OQ; ensuite on pouvait construire ST, trouver le point S, tirer la droite SΩ et marquer ce point V, où cette droite coupait la tangente Rϕ, après quoi la valeur RV de n, correspondant à la valeur donnée AM de x, était connue. De cette valeur on pouvait déduire celle de la soustangente z=nx/a et construire le point L, connaissant le point M où sa tangente coupe l'axe, la longueur 2x de la tangente LM et celle z de la soustangente. , pour RΩ=b=2a, était justement égal à huit fois le carré sur OQ=½a, il suffisait pour cela de choisir IP de telle sorte que IP:RK=MN:OQ; ensuite on pouvait construire ST, trouver le point S, tirer la droite SΩ et marquer ce point V, où cette droite coupait la tangente Rϕ, après quoi la valeur RV de n, correspondant à la valeur donnée AM de x, était connue. De cette valeur on pouvait déduire celle de la soustangente z=nx/a et construire le point L, connaissant le point M où sa tangente coupe l'axe, la longueur 2x de la tangente LM et celle z de la soustangente.
Remarquons encore que ce point L, quoique situé dans la figure de Huygens sur la droite AL, perpendiculaire à l'axe AΩ, doit être considéré comme un point arbitraire de la courbe ABL.
-
voetnoot10)
- Que la réduction de l'aire de la courbe v=b3/b2-n2 à l'aire d'un secteur hyperbolique, employée ici, est au fond identique avec celle du § III de la pièce No. 2661, c'est ce qu'on voit immédiatement en remarquant que les angles Yδα (de la fig. 1 de la pièce No. 2661) et RΩV de la présente figure sont égaux, puisque
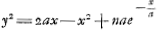 , tandis que le carré sur , tandis que le carré sur 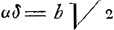 est égal au double du carré sur RΩ=b. est égal au double du carré sur RΩ=b.
-
voetnoot11)
-
Déduction de la construction de Bernoulli, pour le cas GC=2AG. (Voir toujours la figure du § III).
-
voetnoot12)
- Huygens, de cette manière, au lieu de commencer par le calcul de IP (voir le commencement du paragraphe précédent) procède directement au calcul de ST, moyenne géométrique entre RK et IP.
-
voetnoot13)
- On remarquera que l'hyperbole n=4ax-2aa/2x+a se trouve tracée dans la figure 3.
-
voetnoot14)
- Le résultat obtenu, où z représente la soustangente DG de la figure 2, x et a les lignes AG et OT de la même figure, est en effet identique, pour le cas considéré GC=2AG, avec celui formulé par Bernoulli. Voir la Lettre No. 2820.
-
voetnoot15)
- Lisez Hofwijck; maison de campagne de Christiaan Huygens.
-
voetnoot16)
- C'est ce qui a lieu pour le point particulier L, situé sur la perpendiculaire érigée au point A sur l'axe AΩ.
-
voetnoot17)
-
Réduction, pour le cas général GC=θ. AG (fig. 1), du problème de Bernoulli à la aivision en proportion donnée d'une aire hyperbolique.
-
voetnoot18)
- Nous avons emprunté cette équation différentielle, valable pour un point de la courbe supérienre au point T de la figure 2, à la page 54 du livre J. Plus loin, à la page 58, on rencontre une déduction détaillée de l'équation correspondante, avec changement du signe de n et de dn, valable pour la partie inférieure, pour le même cas CG=θ.AG; mais, puisqu'elle procède par les mêmes raisonnements que les déductions des § I et § II, nous avons cru pouvoir nous dispenser de la reproduire. (Voir toutefois la note 4 de la présente pièce). Remarquons seulement que l'n de la formule représente toujours la grandeur az:x.
-
voetnoot19)
- Ce qui va suivre peut être regardé comme une paraphrase du § III, adaptée au cas plus général GC=θ.AG. En effet, pour ce cas les raisonnements de la note 9 restent applicables. Seulement, pour se conformer à l'équation
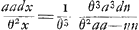 , on doit prendre (fig. 3) AO=OR==a/θ et RΩ=b=θa. Alors QNMO doit être égale à la partie 1/θ3 de RWYΩ, c'est-à-dire à la partie 2/θ3 de RSΩ ou de RKTS. Mais si l'on prend toujours IP:RK=MN:OQ les aires OQMN et RKPI seront dans la raison des carrés sur AO et sur RK=½RΩ√2, c'est-à-dire qu'on aura RKPI=½θ4×NMOQ=θ.RKTS. Connaissant donc IP=aa/x√2 il suffira, pour avoir ST, et ensuite ΩY=n, de savoir diviser l'aire hyperbolique RKPI daus la raison de 1 à θ-1. , on doit prendre (fig. 3) AO=OR==a/θ et RΩ=b=θa. Alors QNMO doit être égale à la partie 1/θ3 de RWYΩ, c'est-à-dire à la partie 2/θ3 de RSΩ ou de RKTS. Mais si l'on prend toujours IP:RK=MN:OQ les aires OQMN et RKPI seront dans la raison des carrés sur AO et sur RK=½RΩ√2, c'est-à-dire qu'on aura RKPI=½θ4×NMOQ=θ.RKTS. Connaissant donc IP=aa/x√2 il suffira, pour avoir ST, et ensuite ΩY=n, de savoir diviser l'aire hyperbolique RKPI daus la raison de 1 à θ-1.
-
voetnoot20)
-
Division d'une aire hyperbolique dans une raison donnée.
-
voetnoot21)
-
Déduction de la construction de Bernoulli pour le cas GC=θ.AG.
-
voetnoot22)
- La signification des deux premiers termes de cette proportion ne nous est pas claire, l'analo- gie avec le commencement du § IV exigeant plutôt pour ces termes x et x
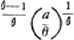 , mais le résultat, en tout cas, est exact. , mais le résultat, en tout cas, est exact.
En effet, la relation: aire RKPI=θ. aire RKTS amène: 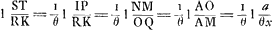 ; donc ST= ; donc ST=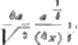
-
voetnoot23)
- Puisque (XZ+ZS)×ZS=qu. Rϕ. Conférez toujours le § IV pour les calculs qui suivent.
-
voetnoot24)
- Puisque n=az:x. La page 54, d'où nous avons emprunté les calculs de ce paragraphe, contient encore quelques formules éparses sans liaison apparente, qui se rapportent à la réduction de cette proportion à celle qui va suivre, où Huygens pour se rapprocher de la solution de Bernoulli a remplacé le paramètre a par l'unité.
-
voetnoot25)
- Remplaçant le θ de Huygens par le n-1 de Bernoulli, et remarquant que l'x représente ladroite AD de la figure de la Lettre No. 2820, on s'aperçoit facilement de l'identité de ce résultat avec celui de Bernoulli tel qu'il est formulé dans la Lettre No. 2820.
|
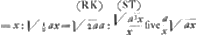 Ga naar voetnoot12).
Ga naar voetnoot12).
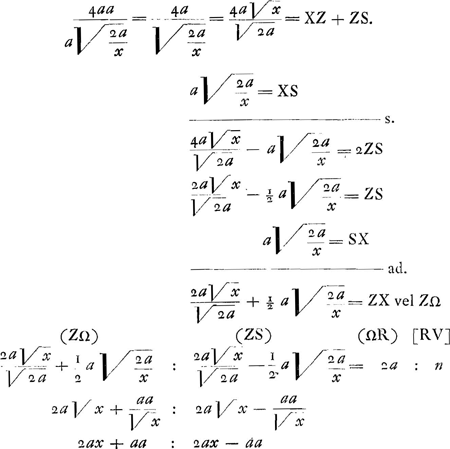
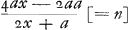 Ga naar voetnoot13)
a:
Ga naar voetnoot13)
a: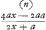 =x:4xx-2ax/2x+a(=z) ἑυρηϰαGa naar voetnoot14) 8 sept. 1693. Hofw.Ga naar voetnoot15)
=x:4xx-2ax/2x+a(=z) ἑυρηϰαGa naar voetnoot14) 8 sept. 1693. Hofw.Ga naar voetnoot15)