Oeuvres complètes. Tome X. Correspondance 1691-1695

N^o 2820.
Christiaan Huygens au Marquis de l'Hospital.
10 septembre 1693.

La minute se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek¹⁾.
La lettre fait suite au No. 2819.
De l'Hospital y répondit par le No. 2825.

A la Haye ce 10 Sept. 1693.

Au M. de l'Hospital.

Ce n'est pas sans apprehender de vous estre importun, Monsieur que je vous ecris celle-cy 8 jours apres ma precedente. Toutefois je n'ay pas voulu manquer

1) Chr. Hugenii etc. Exercitationes Mathematicae, Fasc. l, p. 288.

[p. 498]

de vous faire scavoir que contre mon dessein j'ay meditè sur le Probleme de Mr. Bernoully, qui estant beau me rouloit par la teste et qu'à la fin j'ay trouvè la maniere de le resoudre²⁾. C'est non seulement a fin que vous n'aiez pas la peine de me l'expliquer, comme je vous en avois priè, mais aussi pour vous faire voir que je n'ay pas estè sans profiter de l'honneur de vostre correspondance et enseignements. Je vous ay mandè que la solution de Mr. Jac. Bernoully estoit dans les Acta de Leipsich du mois de Juin, la quelle estant fort courte je la mets icy, parce que peut-estre vous ne l'aurez pas encore vuë. In data pofitione recta AB assignatum est punctum A, et quaeritur curva AC, in qua sumpto ubivis puncto C, ductaque



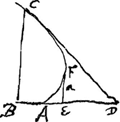per illud recta tangente CD, abscissa AD sit ad tangentem DC in constanti ratione n ad 1. Solutio. Abscissa quavis AD centro D radio DC, qui sit ad abscissam AD ut 1 ad n, describatur arcus circuli, fiatque, ut aggregatum unitatis et dicti radij ad potestatem ± 2n elevati, ad eorundem differentiam, sic ipse radius ad rectam DB auferendam ex positione data AB. Dico si super B erigatur recta BC perpend. ipsi AB, secansque arcum circuli in C, fore punctum C in curva optata AC³⁾.

Je trouve cette mesme construction, par laquelle si n est ½, a quelque ligne prise à discretion et AD ∞ ½ x, on a comme x+a à x-a ou a-x, ainsi CD à DB. Pour y parvenir j'ay rencontrè une equation, où d'un costè estoit Elementum d'un trapeze hyperbolique, de l'autre Elementum d'un espace de la courbe dont l'equation est a³/aa/nn-yy ∞ v, et qui a sa quadrature dependente de celle de l'hyperbole⁴⁾. Ensuite je trouve que la solution demande qu'on puisse diviser

2) Consultez l'Appendice à cette lettre, la pièce N^o. 2821.

3) Posant CD=x, AD=nx et écrivant a pour l'unité, on a donc d'après la solution de Bernoulli: ((x/a)^±2n+1):((x/a^±2n-1)=x:DB, ou bien DB=± x²ⁿ-a²ⁿ/x²ⁿ+a²ⁿ x, où le signe+doit être choisi, pour trouver la valeur absolue, au cas où l'on a CD > a, c'est-à-dire > EF, et le signe - au cas contraire.

4) Consultez les § II, III et V de la pièce N^o. 2821. L'équation rencontrée par Huygens est celle du commencement du § V. En y remplaçant, pour nous conformer à la notation du texte de la présente lettre, n par y, θ par n^-1, elle exprime en effet l'égalité des ‘elementa’ a²n²dx:x et a³dy:(a²n^-2-y²), dont le premier appartient au trapèze hyperbolique OQNM (voir la figure 3 de la pièce N^o. 2821), et dont l'autre est dans une proportion donnée à l'espace ΩRWY, dont la quadrature dépend de celle de l'hyperbole, comme nous l'avons indiqué dans les notes 9 et 10 de la même pièce.

[p. 499]

ou augmenter un trapeze hyperbolique en raison donnée⁵⁾, ce qui se fait geometriquement lors que la raison de CD à DA est de nombre à nombre, mais par la Logarithmique lors que cette raison ne s'exprime que par des lignes⁶⁾. Apparemment j'auray passè par le mesme chemin que vous, Monsieur, car je ne pense pas qu'il y en ait icy plusieurs differens. Au reste ce Probleme contient des choses remarquables et me paroit le plus beau, qu'on ait encore proposè pour la methode inverse des Tangentes. Je vois que Mr. Bernouilly raisonne sur l'utilitè de ces courbes⁷⁾, dont je ne scay si vous avez aussi bonne opinion. J'ay trouvè depuis peu une autre courbe d'un usage qui n'est point douteux et bien d'une autre importance, laquelle je suis obligè par des raisons de tenir encore cachée⁸⁾. En examinant de nouveau la quadrature qu'avoit donné Mr. Leibnitz de la feuille de Des Cartes⁹⁾, j'ay trouvè qu'elle estoit vraie en prenant y comme dans la vostre seconde¹⁰⁾, de sorte que je luy fais reparation d'honneur¹¹⁾.

5) Voir le § V de la pièce N^o. 2821.

6) Voir le § VI de la pièce citée.

7) Jacques Bernoulli, dans l'article cité dans la note 16 de la Lettre N^o. 2819, commence ce raisonnement par la phrase: ‘Eximium autem usum habet hoc Problema. Primo enim hinc constat, infinitas esse diversissimorum generum curvas, communi hac proprietate gaudentes, ut rectae AD, DC, constantem rationem habeant; omnes vero illas esse Geometricas (quanquam aliae aliis magis minusve sint compositae) in quibus hae lineae se habent, ut numerus ad numerum, transcendentales vero omnes, ubi illae non sunt, ut numerus ad numerum’, après quoi il fait suivre le passage cité dans la note 20 de la même Lettre, pour finir par les phrases: ‘Unde patet, si constructiones ejusmodi censendae sunt geometricae & accuratae, aequationes infinitas altissimorum graduum pari cum simplicissimis omnemq; pene fidem excedente facilitate construi posse. Denique nec hoc tacendum, quod solutio hujus problematis abstrusae Methodi Tangentium inversae plurimum perficiendae & promovendae magnum lumen praebere possit’.

8) Consultez la dernière note de la pièce ‘De problemate Bernoulliano’, notre N^o. 2823.

9) Voir la Lettre N^o. 2797, à la page 429.

10) Comparez la Lettre N^o. 2819, à la page 491.

11) Voir la Lettre N^o. 2822, à la page 510.