Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 425]

N^o 2797.
G.W. Leibniz à Christiaan Huygens.
20 mars 1693.

La lettre se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek¹⁾ et C.I. Gerhardt²⁾.
Elle est la réponse au No. 2785.
Chr. Huygens y répondit le 17 septembre 1693.

Hanover ce 10/20 de Mars 1693.

^a) Monsieur

Je commence par le remerciment que je vous dois de ce que vous avés bien voulu me satisfaire si promtement sur mes demandes, touchant le prix pretendu proposé par Messieurs les Estats, qu'un amy me prioit fort de luy faire sçavoir, bien que je luy eusse assez temoigné mon sentiment.

J'avois remarqué moy même dans ma precedente, que je trouvois de la difficulté dans la comparaison de la force centrifuge avec les rayons d'attraction que j'avois proposée, et même j'avois marqué en particulier, en quoy consistoit cette difficulté. Mais je ne croyois pas, qu'on diroit, qu'il n'y a aucune raison de conformité; puisque l'un et l'autre produit une attraction, l'un et l'autre tend du centre à la circonference, l'un et l'autre opere en ligne droite.

Vous dites, Monsieur, que vous trouvés le cours particulier de la matiere dans le tourbillon du soleil, propre à conserver le parallelisme de l'axe de la terre, peu compatible avec le mouvement circulaire en tout sens, qui semble faire la pesanteur vers le soleil. A quoy je reponds, que deux mouvemens semblables à ceux là se trouvent fort compatibles dans le systeme du globe de la terre, ou l'un est la cause de la pesanteur, l'autre celle de la direction magnetique; et cette analogie favorise fort mon hypothese. Et comme il y a une declinaison de l'aimant, dont les causes particulieres nous sont encor inconnues, qui ne sçauroient pourtant se

1) Chr. Huyenii etc. Exercitationes Mathematicae. Fasc. I, p. 152.

2) Leibnizens Mathematische Schriften, Band II, p. 154, et Briefwechsel, p. 711.

a) Rec. le 31 mars [Christiaan Huygens]⁹⁾.

9) Les notes qui suivent ont été écrites d'abord au crayon, la plupart ont été retracées à l'encre, deux ont été effacées au point de devenir illisibles. Plusieurs de ces notes, nommément les notes r, u, v et x doivent avoir été écrites quelques mois après la réception de cette lettre.

[p. 426]

trouver, que dans le cours de quelque matiere, il semble encor, que le detour de l'axe de la terre ne sçauroit venir, que de quelque raison semblable^b). Il est vray, que la terre est un grand corps, dont il n'est pas aisé de changer le mouvement ou la situation; mais comme tous les corps de la nature agissent les uns sur les autres, et qu'il y a plusieurs grands courans particuliers, elle ne semble pas exemte d'accidens; et je ne sçay, s'il seroit conforme à la coustume de la nature, d'abandonner ces grands systemes à ces rencontres. Il semble plustost, que les systemes sont tellement formés et establis par une conspiration de toutes les parties arrangées et asservies de longue main, que les desordres se redressent d'eux mêmes, comme dans le corps d'un animal; ce qui se fait par le cours des corps fluides, qui entretient les solides dans leurs fonctions. Ainsi je m'imagine, que si quelque cause extraordinaire detournoit l'axe de la terre, il reprendroit bien tost sa veritable situation^c); comme fait un aimant; au lieu que, selon l'hypothese de Mons. Neuton la terre vogue dans l'ether, comme feroit une isle slottante, que rien ne dirige, que sa propre tendence déja prise.

Ce que vous dites, Monsieur, qu'une pression uniforme par dehors ne change point la figure d'un corps, et par consequent n'est pas capable d'arrondir une goutte, merite consideration. Mons. des Cartes n'estoit pas de ce sentiment, et en cela j'avois esté du sien; mais je me rendray volontiers, quand je verray comment vous jugés que cela est contraire aux principes de mecanique^d).

Vous jugés aussi, Monsieur, que les tourbillons deferans, ne sont pas conciliables avec les Ellipses de Kepler. Cependant il me semble, que les raisons prises de l'excentricité constante des Planetes, aussi bien que de leurs vistesses dans les aphelies et perihelies^e) ne sont pas sans replique, ou plustost que les tourbillons se peuvent expliquer en sorte, qu'ils favorisent ces choses, bien loin d'y estre contraires. L'objection du passage des Cometes paroist difficile, mais peut-estre, que leur force est telle que le mouvement d'une matiere aussi subtile, que l'est celle du tourbillon ne les detourne pas considerablement; il est bien vray que cette même matiere a assés de force pour conserver le mouvement des Planetes, mais si la Planete estoit reduite en repos dans le tourbillon, le tourbillon ne luy rendroit son mouvement, que peu à peu. Comme dans vos pendules peu de force est capable d'entretenir le mouvement, mais il est plus difficile de le produire.

Je viens à nostre controverse des Atomes, elle est si ancienne, et les esprits y sont si partagés, que je m'etonne nullement, si nous ne tombons pas d'accord là dessus. Cependant comme je croy, que parmy tous ceux, qui ont jamais soustenu les atomes, personne l'a fait avec plus de connoissance de cause, et y a apporté plus de lumieres, que vous, Monsieur, et que de mon costé j'ay taché d'y joindre des considerations assez particulieres, je continue de profiter de vos eclaircissemens. Si l'on devoit supposer des consistences primitives, la question est, s'il seroit plus raisonnable d'aller d'abord à une dureté parfaite et infinie, que d'admettre toute sorte de degrés de fermeté^f) mais tousjours meslés de quelque fluidité, ou mollesse;

b) Voici ce que j'ai dit: Tous les axes devroient estre paralleles [Chr. Huygens].

c) l'axe de la Terre change peu a peu de position [Christiaan Huygens].

d) Je l'expliqueray [Christiaan Huygens].

e) il y a encore les declinaisons constantes [Christiaan Huygens].

f) s'il y a toute sorte de fermetè cela empeschera la vitesse de la lumiere [Christiaan Huygens].

[p. 427]

en sorte que la matiere ait par tout quelque union ou connexion, et que neantmoins elle soit encor divisible par tout. Et qu'ainsi le même corps puisse estre appellé ferme, roide, dur; et encor fluide, mol, flexible, diverso respectu et comparativement, selon l'action qui tache de le flechir ou de le diviser. Vous jugés, Monsieur, qu'il seroit plus difficile de concevoir les raisons de ces differentes fermetés; mais si les fermetés sont primitives, on n'en doit pas chercher la raison. J'avoue que la matiere seroit heterogene en quelque façon, ou plustost dans une varieté perpetuelle, en sorte qu'on ne trouveroit pas la moindre particelle uniforme dans ses parties, au lieu que les Atomes sont homogenes. Mais en recompense la matiere selon mon hypothese seroit divisible par tout, et plus ou moins facilement, avec une variation, qui seroit insensible dans le passage d'un endroit à un autre endroit voisin^g), au lieu que selon les Atomes on fait un saut d'une extremité à l'autre et d'une parfaite incohaesion, qui est dans l'endroict de l'attouchement, on passe à une dureté infinie dans tous les autres endroits. Et ces sauts sont sans exemple dans la nature^h). D'où il s'ensuit aussi, que selon moy la subtilité et varieté va à l'insini dans les Creatures, ce qui est conforme à la raison et à l'ordre (car je suis pour un axiome tout opposé à cet axiome vulgaire, qui dit, naturam abhorrere ab infinito). Mais selon les Atomes le progres de la subtilité et la variation se borne à la grandeur de l'atomeⁱ⁾, ce qui est aussi peu raisonnable que cette autre maniere de borner les choses par des extremités en enfermant le monde dans une boule. Quant à la difficulté des surfaces plattes, par lesquelles les Atomes s'attacheroient, vous repondés, Monsieur, qu'il seroit plustost un grand postulatum de vouloir qu'il y en ait, que de vouloir qu'il n'y en ait point; puisqu'il faut bien de l'exactitude pour en former. Je reponds qu'il faudra tousjours une entiere exactitude pour former quelque surface que ce soit. Quelque qu'elle puisse estre, elle sera exacte^j). Or la surface platte estant des plus simples, il semble que ce qui est cause de l'existence des atomes, seroit encor cause de l'existence des plus simples atomes, à moins que cette cause n'ait eu des raisons particulieres de les eviter, qui ne sçauroient estre prises qu'à fine pour eviter la cohesion. Mais ce seroit assez postuler, que de raisonner ainsi. Vous adjoutés, Monsieur, quand même on admettroit un grand nombre d'Atomes cubiques, qu'ils ne s'attacheroient pas aisement ensemble pour composer des nouveaux corps inseparables, par ce que le plus souvent ils ne reposeroient pas durant quelque temps dans l'attouchement et ne demeureroient qu'un moment dans le même estat, car c'est ainsi que j'entends ce que vous dites, que leur application juste consisteroit in indivisibili^k). Mais je croy qu'il est assez estrange, que cela se peut faire quelques fois, sçavoir qu'ils s'attachent en sorte qu'ils deviennent Atomes, et qu'ils soyent desormais inseparables à toute eternité.

J'avois crû, que ma raison contre les Atomes prise des loix du mouvement estoit une des plus fortes. Cependant puisque vous promettés d'expliquer un jour comment un corps inflexible peut rejallir^l), je ne doute point que vous n'ayés à dire

g) Mon hypothese est plus simple [Christiaan Huygens].

h) ce n'est pas un saut [Christiaan Huygens].

i) cette borne estoit necessaire ou il faloit un progres continuel [Chr. Huygens].

j) il est bien plus facile de former quelque surface indeterminee comme en cassant un corps, que d'en former une exactement platte [Christiaan Huygens].

k) je dis que la position de deux surfaces plattes pour estre appliquées l'une à l'autre consiste in indivisibili. ils ne s'attachent pas pour devenir atomes [Chr. Huygens].

l) voir nos lettres sur cecy [en crayon, Christiaan Huygens].

[p. 428]

la dessus des choses tres considerables à vostre ordinaire. Vous trouvés aussi, que la difficulté pourroit estre retorquée contre moy, puisque les corps à ressort sont composés, et que par consequent les derniers petits corps estans sans ressort seront aussi incapables de rejallissement. Mais je reponds qu'il n'y a point de dernier petit corps^m) et je conçois qu'une particelle de la matiere, quelque petite qu'elle soit, est comme un monde entier, plein d'une infinité de creatures encor plus petites; et cela à proportion d'un autre corps fut il aussi grand, que le globe de la terre.

Comme il semble qu'on ne sçauroit rendre aucune raison, pourquoy les parties d'un atome sont inseparables, que parce quelles se touchent une fois parfaitement par leur surfaces durant quelque temps; c'est pour cela que, j'ay dit, que dans l'Hypothese des Atomes l'attouchement fait l'office d'un glutenⁿ⁾. Il semble aussi que si l'attouchement par surfaces fait une connexion infiniment forte; l'attouchement par lignes et par points deuroit aussi faire des connexions, mais surmontables^o) en sorte que deux corps se touchant par des lignes plus grandes seroient plus³⁾ aisés à separer, et des corps se touchant par plus de points auroient plus de connexion que ceux qui se toucheroient par moins de poincts caeteris paribus. Et mêmes, point contre point, et ligne contre ligne, il semble que contactus osculi deuroit donner plus de connexion que simplex contactus. De plus, si un attouchement superficiel durable faict un attachement insurmontable, il semble qu'un attouchement momentanée feroit une connexion surmontable^p), mais plus forte, selon que le corps, qui rase l'autre en le touchant, a moins de vistesse. Enfin quoy que j'aye parlé cy dessus des fermetés ou consistences primitives, j'ay tousjours du panchant à croire, qu'il n'y en a aucune primitive, et que le seul mouvement fait de la diversité dans la matiere^q) et par consequent la cohesion. Et tant que le contraire n'est pas encor demontré, il me semble, qu'on doit eviter la supposition d'une telle nouvelle qualité inexplicable, laquelle estant accordée, on passeroit bientost à d'autres suppositions semblables, comme à la pesanteur d'Aristote, à l'attraction de Mons. Neuton, à des sympathies ou antipathies et à mille autres attributs semblables.

Mr. le Marquis de l'Hospital m'a fait l'honneur de me communiquer sa belle invention de la rectification de la Courbe Logarithmique^4)r). Cela fait voir qu'il a fait des tres grands progrés dans cette Analyse superieure^s). Et j'espere de luy des lumieres considerables, je voy le moyen de trouver tousjours la ligne ex data

m) mais qu'est ce que le ressort a vostre opinion? [Christiaan Huygens].

n) cet attouchement fait l'unité; rien n'estant entre deux [Christiaan Huygens].

o) consequence sans fondement [Christiaan Huygens].

3) Il faut évidemment lire: moins.

p) plustost point de connexion [Christiaan Huygens].

q) je ne comprens point cette idée [Christiaan Huygens].

4) Il l'a fait dans une lettre du 14 décembre 1692, publiée par C.J. Gerhardt dans ‘Leibnizens Mathematische Schriften’, Band II, p. 216. L'exposé du ‘problème’ et de la ‘solution’ y correspond presque littéralement avec celui qu'on rencontre dans la Lettre N^o. 2775, jusqu'aux mots: ‘2^o. Si l'on prent TR’.

r) Bernoulli se l'attribue¹⁰⁾ [Christiaan Huygens].

10) Consultez, sur cette note, les lettres de Huygens à de l'Hospital du 5 et celle de l'Hospital à Huygens du 10 août 1693.

s) touchant notre correspondance [en crayon, Christiaan Huygens].

[p. 429]

quantitate subtangentis, lorsque cette ligne est ordinaire^t). Mais je n'ay pas encore le loisir et la patience necessaire pour mettre en estat tout ce qu'il faut pour practiquer cette methode, et en attendant je suis reduit à me servir de quantité d'adresses particulieres, à peu prés comme on faict pour resoudre des problemes semblables à ceux de Diophante.

Quant à la courbe de M. de Beaune, dont la soutangentielle seroit yy-xy:a, je l'ay voulu considerer presentement, parce qu'elle est simple et je trouve, qu'elle depend de la courbe des Logarithmes en telle façon, que le logarithme estant y, x sera la difference entre le logarithme et la subnumerale. J'appelle icy la sousnumerale z, supposé que le nombre du logarithme est le quotient d'a divisé par a-z⁵⁾.

Il faut avouer, Monsieur, que vos decouvertes sur la quadrature de la galande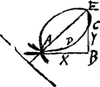



de Mr. de Roberval sont extremement belles, j'entends la ligne dont l'equation est x³+y³=nxy. Comme cette ligne est d'une nature simple, et que les coordonnées y sont homoeoptotes comme dans le cercle, j'ay aussi voulu tacher, si j'en pourray trouver la quadrature, et j'en ay ensin trouvé cette construction generale^u) que le triligne ABCDA est à ⅔ ny-½xx comme le quarré de l'abscisse x, ou AB, est au quarré de l'ordonnée y ou BC⁶⁾.

Je n'ay garde de m'attribuer par avance la connoissance de cette source nouvelle, que vous avés trouvée pour quantité de problemes des quadratures et des subtangentes. Il se pourroit que j'en sçusse quelque chose, mais je craindray plustost que non; car je voy qu'on peut employer quantité d'adresses particulieres, et je ne doute point, qu'il n'y en ait beaucoup, qui me sont inconnues, quoy qu'il y en ait aussi beaucoup que j'ay employées en temps et lieu. Je me sers quelques fois avec succes des series infinies, Car toutes les fois qu'on donne un probleme tan-

t) Donnez luy une soustangente deguisee¹¹⁾ [Christiaan Huygens].

11) Huygens en a proposé dans sa réponse du 17 septembre 1693.

5) C'est-à-dire ; solution correcte.

u) Cette construction n'est pas vraie que lors que EB se prend pour x, et AB pour y [Christiaan Huygens].

6) On aurait donc, d'après Leibniz, aire , c'est-à-dire, après substitution dans le second terme de la valeur x³=nxy-y³, aire , ce qui est faux évidemment puisque cet aire ne peut pas excéder celle du triangle ABC. Huygens n'a pas manqué de remarquer cette méprise, comme on le voit par le contenu du lambeau de papier que nous avons reproduit dans la dernière note de la présente lettre. Huygens y substitue, dans la proportion indiquée par Leibniz, la valeur véritable ½xy-⅙nyy/x de l'aire du triligne, telle qu'il pouvait la déduire facilement au moyen du résultat mentionné dans les dernières lignes de la pièce N^o. 2793, ce qui conduit à une absurdité. Ce n'est que plus tard (voir sa lettre à de l'Hospital 10 septembre 1693 et celle à Leibniz du 17 septembre 1693) qu'il découvrit que la formule de Leibniz devenait correcte si on l'applique au mixtiligne AEBA, en posant EB=y. Voir encore la figure de la note 13.

[p. 430]

gentiel, je puis trouver la courbe demandée per seriem infinitam. Ce qui est au moins de grand usage pour la practique^v). Car je suppose y=a+bx+cx²++dx³+ex⁴ etc. et par consequent j'ay aussi yy, y³ etc. item xyy, xy³, x²y² etc. j'ay aussi dy. Car dy est égal à dx multiplié par b+2cx+3dx²+4ex³ etc. et ddy est égal à 1. 2c+2. 3dx+3. 4. ex² etc. multiplié par dx² et ainsi de suite. Ayant donc mon equation differentielle delivrée des fractions, racines et sommes, et ordonnée en sorte, qu'elle soit egale à rien, et ayant expliqué les termes où entre y ou dy, en sorte, qu'il ne reste d'autre indeterminée que x, ce qui fait evanouir dx, j'explique les arbitraires, a, b, c, etc. en sorte que tous les termes se detruisent, et par ce moyen je trouve leur valeur, et par consequent celle d'y. Cette methode est la plus generale qu'on puisse imaginer, car elle reussit pour tous ces problemes et encor pour ceux, dont la difficulté est d'une transcendance du second, troisiême ou autre degré, c'est à dire, qui va aux differentio-differentielles et au delà. En un mot est supplementum Generale Geometriae practicae pro Transcendentibus; pour ne dire (ce qui paroist assez) qu'elle sert à donner les racines des equations, mais aussi elle sert souvent à trouver des valeurs finies^w). J'espere le plaisir d'apprendre un jour vostre maniere physico-mathematique pour la quadrature de l'Hyperbole^x). Ces applications donnent souvent des nouvelles vues.

Voicy quelque chose de tout autre nature, que je joins icy. J'ay eu en main quantité de pieces curieuses qui servent à l'Histoire et aux affaires, dont je feray imprimer le recueil. Celuy des plus anciennes avant l'an 1500, paroistra ce printemps dans un volume in fol⁷⁾. Mais pour les modernes, particulierement de nostre siecle, je souhaitterois encor bien des choses.

Monsieur vostre frere et quelques autres habiles hommes de vostre pays, employés dans les affaires publiques, me pourroient favoriser en ce dessein à vostre recommandation, en communiquant quelques pieces curieuses, qui serviroient à instruire le public, sans faire prejudice à qui que ce soit.

C'est dommage que Mons. van Beuninguen n'est pas en estat d'y contribuer⁸⁾.

v) Je n'estime guere les series que quand elles se terminent comme de Greg. Newton Hospital¹²⁾ [Christiaan Huygens].

12) Voir, à propos de cette remarque, la lettre de Huygens à de l'Hospital du 23 juillet 1693 et la réponse de de l'Hospital du 10 août 1693.

w) Ce serait le plus beau [Christiaan Huygens].

x) Vous l'aurez vue. Elle a donné occasion a Bernoulli pour d'autres¹³⁾ [Christiaan Huygens]¹⁴⁾.

13) Consultez la Lettre à de l'Hospital du 3 septembre 1693.

14) A cette lettre de Leibniz se trouve joint un lambeau de papier sur lequel Huygens a noté ce qui suit:
‘Selon Mr. Leibnitz il y auroit cette proportion veritable.
Triligne ABCDA
qu. AB qu. BC
Aeq.o curvae x3+y3 ∞ nxy y3 ∞ nxy-x3 ½xx ½xx -⅙ny4 ∞ ⅙ nyx3 absurdum.
Mr. Leibnitz se trompe donc. Il devoit mettre [voir la Lettre No. 2801]. Il dira qu'il l'a oubliè ou son copiste.
Il ne se trompe point si AB est x, EB y.
Lelogarithme estant y, x sera la difference entre le logarithme et a-aa/n l'excès de la soutangente sur aa divisè par le nombre du logarithme. C'est ainsi qu'il devoit dire suivant ce que montre la construction seconde du Marquis de l'Hospital, ou bien le logarithme estant y, x sera la difference entre le logarithme et z (qui est FA, je ne scay pourquoy il l'appelle sounumerale) si le nombre du logarithme est ∞ aa/a-z, et non a/a-z. Il aura vu la solution de M. le Marquis de l'Hospital dans le Journal de Scav. de Sept. 1. 92’. [Voir la note 2 de la Lettre No. 2787 et la Lettre 2801].

7) Il s'agit de l'ouvrage:
Codex Juris Gentium Diplomaticus, In quo Tabulae Authenticae Actorum Publicorum Tractatuum, aliarumque rerum majoris momenti per Europam gestarum, pleraeque ineditae vel selectae, ipso verborum tenore expressae ac temporum serie digestae, continentur; A fine seculi undecimi ad nostra usque tempora aliquot Tomis comprehensus: Quem ex Manuscriptis praesertim Bibliothecae Guelfebytanae Codicibus, Et Monumentis Regiorum aliorumque Archivorum, ac propriis denique Collectoreis Edidit G.G.L. Hanoverae, Literis & Impensis Samuelis Ammonii. M DC XCIII, in-f^o.
La publication de ce livre paraît avoir été hâtée par l'éditeur. Après la mention faite des titres de deux documents dont la teneur n'est pas donnée, l'ouvrage se termine par la remarque: ‘Haec aliaque imminentes Nundinae Typographum festinantem in sequentia differre coegerunt.’

8) Voir la Lettre N^o. 2766, note 6.

[p. 431]

Mais vous ne manqués pas d'habiles ministres, et souuent les heritiers de ceux qui ont esté employés autrefois ne sont pas chiches de telles choses.

Je vous demande pardon de la liberté que je prends de vous parler d'une chose de cette nature. C'est à condition que cela ne vous importune nullement et que vous ne fassiés que ce que vous pourrés commodement, par le moyen de quelques amis, un mot de vostre part valant mieux, que les grandes sollicitations de beaucoup d'autres. Je suis avec zele etc.

Monsieur

Vostre treshumble et tres obeissant seruiteur Leibniz.

9) Les notes qui suivent ont été écrites d'abord au crayon, la plupart ont été retracées à l'encre, deux ont été effacées au point de devenir illisibles. Plusieurs de ces notes, nommément les notes r, u, v et x doivent avoir été écrites quelques mois après la réception de cette lettre.

10) Consultez, sur cette note, les lettres de Huygens à de l'Hospital du 5 et celle de l'Hospital à Huygens du 10 août 1693.

11) Huygens en a proposé dans sa réponse du 17 septembre 1693.

12) Voir, à propos de cette remarque, la lettre de Huygens à de l'Hospital du 23 juillet 1693 et la réponse de de l'Hospital du 10 août 1693.

13) Consultez la Lettre à de l'Hospital du 3 septembre 1693.

14) A cette lettre de Leibniz se trouve joint un lambeau de papier sur lequel Huygens a noté ce qui suit:
‘Selon Mr. Leibnitz il y auroit cette proportion veritable.
Triligne ABCDA
qu. AB qu. BC
Aeq.o curvae x3+y3 ∞ nxy y3 ∞ nxy-x3 ½xx ½xx -⅙ny4 ∞ ⅙ nyx3 absurdum.
Mr. Leibnitz se trompe donc. Il devoit mettre [voir la Lettre No. 2801]. Il dira qu'il l'a oubliè ou son copiste.
Il ne se trompe point si AB est x, EB y.
Lelogarithme estant y, x sera la difference entre le logarithme et a-aa/n l'excès de la soutangente sur aa divisè par le nombre du logarithme. C'est ainsi qu'il devoit dire suivant ce que montre la construction seconde du Marquis de l'Hospital, ou bien le logarithme estant y, x sera la difference entre le logarithme et z (qui est FA, je ne scay pourquoy il l'appelle sounumerale) si le nombre du logarithme est ∞ aa/a-z, et non a/a-z. Il aura vu la solution de M. le Marquis de l'Hospital dans le Journal de Scav. de Sept. 1. 92’. [Voir la note 2 de la Lettre No. 2787 et la Lettre 2801].