Oeuvres complètes. Tome X. Correspondance 1691-1695

N^o 2823.
Christiaan Huygens aux Editeurs des Acta Eruditorum.
[septembre 1693].
Appendice I au No. 2822.

La minute se trouve à Leiden, coll. Huygens.
La pièce a été imprimée dans les Acta Eruditorum d'octobre 1693¹⁾.

^a) C.H.Z. de Problemate Bernouliano in actis Lipsiensibus hujus anni pag. 235 proposito²⁾.

Elegans inprimis esse hoc Problema, cum ex iis quae Clarissimus inventor³⁾ de eo prodidit, tum ex solutione et commentatione fraterna⁴⁾ manifestum est.

1) Elle y est accompagnée d'un article de Leibniz que nous reproduisons dans le N^o. 2824.

a) Missa ad Leibnitium 17 Sept. 1693.

2) Consultez la note 4 de la Lettre N^o. 2807.

3) La minute a: auctor.

4) Voir l'article cité dans la note 16 de la Lettre N^o. 2819.

[p. 513]

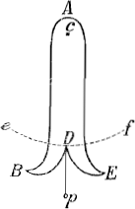
A quo investigando cum propter insignem difficultatem, quae statim sese offerebat, abstinere statuerim⁵⁾, (neq; enim omnibus perquirendis, quae a Viris eruditis exercitii gratia proponuntur, incumbere necesse existimo, aut assequendis parem me profiteor) non desiit tamen quasi invitum compellere recurrens identidem quaesiti non vulgaris idea, donec tandem quod desiderabam obtinui⁶⁾. Inventa nimirum aequatione differentiali in qua ex altera parte erat elementum trapezii hyperbolici, ab asymptoto perpendicularibus intercepti; ab altera elementum spatii curvilinei, quod itidem ad trapesium hyperbolicum reduci posset⁷⁾. Quod apertius exponerem, nisi relinquendam etiamnum aliis putarum inquirendi voluptatem. Inde eo rem deducebam, ut trapezium ejusmodi hyperbolicum secandum esset aut augendum secundum rationem datam⁸⁾. Quod cum per medias aut continue proportionales fieri possit, ubi ratio tangentis ad abscissam est ea quae numeri ad numerum, hinc apparuit curvam quaesitam tunc iis accensendam quae geometricae vocantur, alias esse ex heterogeneis; ac tamen constructionem dari posita lineae logarithmicae descriptione⁹⁾, quam quidem hic adducerem, nisi viderem haud difficulter ex ipsa Jacobi Bernoullii doctissima simul brevissimaque solutione omnia¹⁰⁾ erui posse; ut jam ab alijs occupatam dubitem¹¹⁾.

Colligitur vero ex his illud animadversione dignum, nempe quandocunque in investigatione curvarum ex tangentibus aut subtangentibus ejus, ad similes ei quam dixi aequationes pervenietur, aut in quibus habeatur utrinque elementum spatii ad trapezium hyperbolicum reductibilis; tunc idem hoc, quod mirabile hic accidit, eventurum, ut curvae geometricae diversorum generum graduumque existant, si hyperbolarum ad quas devenitur rectangula quae in asymptotis, fint commensurabilia. Praeterea observanda venit in hoc problemate inusitata ac singularis analysis via, quae ad alia multa in hac Tangentium doctrina aditum aperit, ut egregie jam animadvertit Vir celeberrimus calculi differentialis inventor, sine quo vix esset, ut ad hasce geometriae subtilitates admitteremur. Porro quod ad curvarum, de quibus agitur, designationem in plano attinet, possem, si operae pretium esset, alios modos ac fortasse commodiores indicare¹²⁾ quam qui a Cl. Bernoullio praescri-

5) Lisez, conformément à la minute: statuissem, (d'après les ‘Corrigenda’, communiqués dans les ‘Acta’ de juillet 1694, p. 338), et consultez la Lettre N^o. 2819, à la page 494.

6) Voir la Lettre N^o. 2820, et la pièce N^o. 2821.

7) Voir la note 4 de la Lettre N^o. 2820.

8) Voir le § V de la pièce N^o. 2821.

9) Voir le § VI de la pièce N^o. 2821.

10) Lisez: eam, comme l'ont aussi la minute et les ‘Corrigenda’.

11) Huygens, toutefois, est revenu sur cette construction dans l'article des ‘Acta’ de septembre 1694, intitulé: ‘C.H.Z. Constructio universalis Problematis a Clarissimo Viro, Joh. Bernoullio, superiori anno mense Majo propositi’. Voir la correspondance de 1694.

12) Voir, sur ces descriptions mécaniques de la courbe de Bernoulli, la lettre de Huygens à de l'Hospital du 5 novembre 1693.

[p. 514]

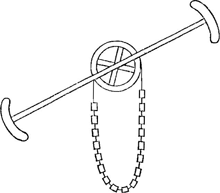
bitur¹³⁾, atque etiam docere qua ratione optime peragatur descriptio nostrae quadratricis hyperbolae, quae inter Tractorias (ita enim vocari possunt) simplicissima censenda est, cum ad eam filis nihil opus sit, sed bacillo tantum utrimque cuspidem lateri infixam habente, quo fit ut & regressu explorari possit quam recte exarata sit¹⁴⁾. Sed his supersedendum arbitror, donec insignis usus aliquis harum linearum in lucem proferatur. Interim aliam quandam utilissimam curvam nuper mihi repertam Geometrae sciant, cujus opera horologiis aequalis motus consiliatur, ac ejusmodi ut maris agitatione nequaquam turbari aut imminui¹⁵⁾ queat¹⁶⁾; quod

13) Consultez, sur cette description de Bernoulli, la note 20 de la Lettre N^o. 2819.

14) Consultez, sur la tractrice et sa description mécanique, la pièce N^o. 2793, aux pages 408-413.

15) La minute a: extingui.

16) Le succès au premier abord douteux de la nouvelle expérience pour déterminer la longitude sur mer au moyen des horloges à pendule (voir la Lettre N^o. 2785, à l'endroit marqué par la note 3) et les vains efforts subséquents pour déduire quelque résultat satisfaisant des données que J. de Graaff avait recueillies dans son voyage du Cap (voir les N^os. 2786, 2789, 2798, 2800, 2802 et 2803) paraissent avoir induit Huygens à rechercher d'autres moyens pour réaliser des mouvements périodiques isochrones, qui seraient à l'abri des perturbations extérieures, telles que celles produites par le roulement et le tangage des vaisseaux de haute mer.
Les essais tentés par Huygens dans cette direction remplissent plusieurs pages des livres H et J des Adversaria. Déjà Uylenbroek, dans le deuxième Fascicule des ‘Exercitationes Mathematicae’ pp. 160 à 170, en a donné un extrait. C'est même à cette partie des travaux de Huygens qu'il a emprunté la page des Adversaria reproduite en facsimilé, qui termine son ouvrage. Nous nous proposons de donner tout ce que les Adversaria contiennent de remarquable à ce sujet dans la partie de notre publication qui renfermera les ouvrages inédits de Huygens.
Ici, nous nous bornons à indiquer succinctement comment, dans cette recherche, Huygens a été conduit à la courbe proposée à la fin de la présente pièce N^o. 2823.
Pour trouver ce que Huygens appelle ‘le Balancier marin parfait’ il part du principe que le mouvement pendulaire isochrone se produit lorsque le moment de la force directrice est à chaque instant proportionnel à l'écart de l'état d'équilibre.
Huygens essaie donc d'abord la disposition de la figure 1, où le sil sans fin, suspendu dans

la gorge d'une poulie fixée au balancier, porte des petits poids égaux et équidistants. L'essai de cet appareil, inventé le 13 janvier 1693, n'a pas été satisfaisant. Les grandes oscillations se montraient plus lentes que les petites, ce que Huygens attribue principalement à deux causes: savoir, que dans les oscillations plus étendues 1^o. la résistance de l'air se fait sentir plus fortement, et 2^o. le nombre de poids qui doivent se plier est plus grand, en même temps

que l'angle que décrit chaque poids en tournant. C'est pour remédier à ce dernier inconvénient que Huygens imagine les formes de chapelet des figures 2 et 3; tandis que pour obvier au premier il emploie la forme de balancier de la figure 4.
Le 6 mars suivant il paraît avoir abandonné ce système pour s'arrêter au suivant. A l'axe d'un balancier (fig. 5) est attachée une languette en métal, de la forme ABDE, dont les bords DB et DE doivent être taillés de manière qu'un poids p suspendu par un fil ou ruban au point D, et qui dans le mouvement oscillatoire du balancier s'enroule ou se déroule sur ces bords, produise à chaque instant un moment de force, par rapport à l'axe C, qui soit proportionnel à l'écart angulaire de la position d'équilibre de la languette.
Huygens démontre que la courbe qui satisfait à cette condition est la développante du cercle eDf décrit du centre C et que, dans ce cas, le poids p, lorsque le fil reste vertical, décrit une parabole.

[p. 515]

in pendulis nostris hactenus usurpatis non satis caveri potuit. Adco ut nova ac certior spes nunc affulgeat perficiendi Longitudinum inventi.

Curva haec formatur.

a a b b c d e e e e e f i i i i i l l l m m m m n o r r s s t t u u x^b)

b) Dans la minute Huygens écrivit:
Flexilis ambitum cum linea deserit orbem en ajoutant en marge: literas confusas misi hujus versus.