|
| |
No 2819.
Christiaan Huygens au Marquis de l'Hospital.
3 septembre 1693.
La minute se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. UylenbroekGa naar voetnoot1).
La lettre est la réponse au No. 2815.
De l'Hospital y répondit par le No. 2825.
Hofwijck 3 Sept[embre] 1693.
J'ai receu, Monsieur, celle que vous m'avez fait l'honneur de m'escrire du 10 aoust. Vous aurez aussi receu la miene du 5 du mesme la quelle, si on vous
| |
| |
l'eut apportée un peu plustost, vous auroit epargnè la peine de m'expliquer ce qui regarde l'invention de la courbe dont la soutangente est x- y, dont je ne laisse pas de vous estre obligè. Pour mes autres doutes, vous verrez dans la mesme lettre que j'ay aussi trouvè par vostre regle, comment faire les sommes dans vostre premiere quadrature de la fcuille de des Cartes. Et pour ce qui est de la difficultè touchant la 2 e j'ay trouvé du depuis que lors qu'on prend BE pour y, les sommes
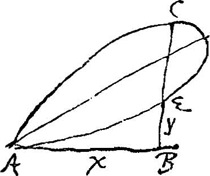
de-2 a3dz/3 zz et+ a4dz/ z3 dans vos positions, ne sont pas+⅔ axx/ y-½ x4/ yy, mais ⅔ axx/ y-⅔ aa et-½ x4/ yy+½ aa, qui font ⅔ axx/ y-½ x4/ yy-⅙ aa, de sorte que ces sommes ne se prenent pas comme à l'ordinaire, mais demandent qu'on y emploie d'autres moiens et d'autres considerations Ga naar voetnoot2), ce que sans doute vous aurez aussi remarquè, et qu'il faut rectifier de mesme vostre 1. re maniere lors qu'on y veut trouver l'aire de l'espace ACB.
Je m'estois aussi satisfait, devant que de recevoir vostre derniere lettre, sur la difficultè que je trouvois à reduire l'equation differ.lle mdy ∞ ½ydm+½mdm à dn ∞ ½m-½dm, en supposant y ∞ nm½. Ca estè en me resouvenant que √mm+mdm est ∞ m+½dm. Car cela m'a aidè à demesler ce changement d'equationGa naar voetnoot3), dans lequel autrement je n'entendrois pas la raison de ce que le
| |
| |
calcul differentiel produit. J'avois trouvè en supposant y ∞ nmb que dy ∞ ∞ mb dn+bnmb-1 dm, mais qu'en supposant y ∞ na mb, il vient dy ∞ ∞ amb na-1 dn+bna mb-1 dm, je ne le vois pas encore, apparemment par ce que je ne suis pas assez versè dans le calcul Exponentiel, qui me paroit difficile et fatigantGa naar voetnoot4).
Pour ce qui est des suites pour la quadrature, voicy celle de Mr. GregoriGa naar voetnoot5). Quand l'equation de la courbe est l ∞ bxr×(sxn+a)m l'area est:
| (sxn+a)m+1×b×s-1×xr+1-n/mn+r+1+(n-r-1)×ba×s-2×xr+1-2n/(mn+r+1)×(mn+r+1-n) |
| +(n-r-1). (2n-r-1)×ba2×s-3×xr+1-3n/(mn+r+1)×(mn+r+1-n)×(mn+r+1-2n) etc. |
où il faut scavoir que comme le premier terme est multipliè par (sxn+a)m+1, ainsi tous les autres le doivent estre de mesme.
Il est evident que cette series est terminée lors que r+1 ∞ n ou ∝ 2n, ou ∞ 3n etc., c'est-à-dire lors que r+1/n est un nombre entier et positif, et qu'alors on a la quadrature parfaite. Ce que je vois estre de mesme dans vostre seconde
| |
| |
suite car vostre c est r+1/n. Mais d'ailleurs il y a de la difference, comme vous verrez Monsieur en comparant seulement le premier terme de celle de Gregori, qui, en negligeant les s, est b×(xn+a)m+1×xr+1-n/mn+r+1 avec le premier des vostres, zm+c/n×1/m+cGa naar voetnoot6) ou bien (xn+a)nm+r+1/n/mn+r+1 parce que vous posez z ∞ xn+a et c ∞ r+1/n. Je vous laisse à examiner cette difference, et si vostre suite est sans faute, ce que vous verrez en essaiant quelque quadrature connue, où l'aire embrasse deux ou plusieurs termes. Car lors qu'elle ne consiste que dans le premier, c'est-à-dire quand r+1 ∞ n, vos quadratures s'accordent. Je suis assurè de celle de Mr. Gregori aussi dans les autres casGa naar voetnoot7), mais la vostre seroit plus simpleGa naar voetnoot8). Vostre premiere suite est encore
très considerable, pouvant servir, ainsi que vous le remarquez, lors que l'autre est sans effet, pourvu que vostre m soit un nombre entier et positif. Mr. Gregori ne m'a point parlè d'une suite pareille à celle-là, ni aussi de la 3.e, de la quelle aussi bien il n'a pas besoin. Et je crois qu'elle ne vous est pas necessaire non plus, parce qu'on peut sçavoir d'ailleurs la valeur de ses termes, qui ne constituent qu'une quantité connueGa naar voetnoot9).
J'avoue que la Regle de Mr. Fatio est fort bornée, mais elle ne laisse pas d'avoir son usage, et il faudroit voir si elle ne sert pas quelquefois dans de rencontres où la vostre ne succede point. Au reste le deguisement des soutangentes, où ni l'une ni l'autre à ce qu'il semble n'ont lieu, se fait de cette maniere, sçavoir en substituant dans quelque terme d'une soutangente la valeur de x ou y, née d'un terme de l'Equation de la courbe, dont ce mesme terme de la soutangente n'est point procedé. Par ex. si dans la soutangente 2yy/2a-2x ou yy/a-x, qui est tirée simplement de l'equation du cercle 2ax-yy-xx ∞ 0, on substitue pour-x, sa valeur-xx-yy/2a qui est née du terme 2ax, et non pas du terme-xx d'ou estoit procedè ce-x dans le diviseur, il viendra la soutangente 2ayy/2aa-yy-xx, et de
| |
| |
là l'equation differentielle intraitable 2aadx-yydx-xxdx-2aydy ∞ 0Ga naar voetnoot10). La mesme chose arrive par de semblables substitutions heteroclites dans des soutangentes desià deguisées, mais traitables. Et souvent en substituant derechef dans les intraitables, elles redevienent traitables, comme dans cette intraitable en substituant pour 2a dans 2ayy sa valeur yy+xx/x. Je fis ces observations en m'exerçant avec Mr. Fatio à faire des essais de sa RegleGa naar voetnoot11). Je n'en ay pas encore recherchè à fond les raisons, qu'il seroit bon de scavoir, quoy qu'il semble que presque jamais ces soutangentes intraitables ne s'offrent par quelque proprietè de tangente donnée, mais seulement en faisant de ces deguisements extraordinaires tout expres.
La Regle de Mr. Leibnitz ne scauroit vous estre inconnue, qui reduit l'invention des courbes par leur soutangente aux quadratures, dont vous m'avez parlè cy-devant; comme, lors que la soutangente est aa/√aa-xx, la construction de la Courbe est reduite aux quadratures du cercle et de l'hyperboleGa naar voetnoot12). Elle est bornée en ce qu'elle n'a lieu que lors que la soutangente est produite par la multiplication ou division de deux quantitez qui ne contienent que x ou y et non pas les deux à la fois. Elle est utile en plusieurs cas, mais quelque fois elle mene à des quadratures difficiles la où la methode de Mr. Fatio donne d'abord l'equation de la courbeGa naar voetnoot13).
Vous aurez vu dans ma precedenteGa naar voetnoot14) que j'ay estè etonnè du procedè de Mr. Bernoulli le medecin à vostre egard. Maintenant apres ce que vous m'en dites, j'en suis scandalizè, car s'il a esté faschè de ce qu'aiant donnè la solution du Probleme de Mr. de Beaune, vous n'avez pas fait mention de luy, il pouvoit dire ce qui en estoit, sans faire de supercherie.
Le Probleme qu'il a proposè publiquementGa naar voetnoot15) a estè resolu par son frere a ce que je vois dans les Acta de Leipsich, du mois de JuinGa naar voetnoot16), que je reçus avanthier. Je n'avois pas cru qu'il en scut tant, car jusqu'icy il me semble bien difficileGa naar voetnoot17). Il n'explique pas comment il est parvenu à la solution ce que j'attens de vous
| |
| |
Monsieur, car je ne me pique pas de le trouver moy mesme. Vous vous souviendrez aussi s'il vous plait de me faire part de vostre 3.e maniere de mesurer la Feuille de Des CartesGa naar voetnoot18).
Il paroit assez, et mesme M. Bernouilli l'avoueGa naar voetnoot19), que cette courbe de son
| |
| |
frere est inventée à l'occasion de ma Tractoria qui estoit au Journal de Rotterdam. La description estoit de la mesme natureGa naar voetnoot20), la quelle je puis donner de plus d'une façonGa naar voetnoot21) et qui soient meilleures que celle qu'il propose.
Je trouve dans les dits Acta de Juin une longue Exercitation du mesme Mr. BernouilliGa naar voetnoot22) touchant ces courbes qu'ils appellent Causticas et Diacausticas, qui à mon jugement sont fort peu de chose. Et ce n'a estè que parce qu'elles s'offroient d'elles mesmes que j'en ay touchè quelque chose dans mon Traitè de la LumiereGa naar voetnoot23) Ce fut plusieurs années devant que Mr. Tchirnhaus donna sa fausse construction de la caustica du miroir concaveGa naar voetnoot24) dans le Journal des Sçavants, la quelle demeura sans correction jusques en 1690, lors que ayant envoyè mon dit Traitè à Messieurs les autheurs des Acta, Mr. Tchirnhaus y apprit la veritable construction de cette courbe, et a fin qu'il ne parut pas qu'il l'eust de moy, et pour passer pour l'Inventeur de ces lignes, il fit en sorte
qu'on ne parla point dans les acta de mon traitè qu'un an après. Il avoit vu la figure de cette Caustica du miroir spherique dans mon manuscrit, m'estant venu voir a Paris et voila M. de ces gens dont vous parlez, a l'occasion de ce qui vous est arrivè.
Mais ma lettre devient trop longue. Je finis apres vous avoir fait une seule demande, scavoir si vous estes bien persuadè de ce que Mr. Bernouilli a avancèGa naar voetnoot25) que la courbe de la voile est la mesme que la Funicularia, touchant quoy je vois que Son frere vous allegueGa naar voetnoot26). Il me semble que j'avois trouvè que cela estoit
| |
| |
autrement, mais vostre authoritè fera pour le moins que je repete l'examenGa naar voetnoot27). Je suis avec respect et devotion entiere &c.
Je suis fachè de voir qu'on ait mis dans les Traitez de l'Academie des SciencesGa naar voetnoot28) une construction du Probleme d'Alhazen, que je ne me souviens point d'avoir donnéeGa naar voetnoot29) et non pas une beaucoup meilleure imprimée autrefois dans le Journal de LondresGa naar voetnoot30), qui est la mesme que Mr. Ozanam a du depuis inserée dans son dictionaireGa naar voetnoot31), mais mon analyse et demonstration estoient beaucoup plus courtes. |
-
voetnoot1)
- Chr. Hugenii etc. Exercitationes Mathematicae Fasc. I, p. 283.
-
voetnoot2)
- On trouve ces considérations à la page 38 du livre J sous la suscription: ‘Tollitur difficultas de qua pag. sequ. [voir, p. 454, la note 5 de la Lettre No. 2807]. Et colliguntur verae summae
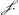 -2a3dz/zz+a4dz/z3.’ On y voit comment Huygens, en comparant la substitution z=a2yx-2, employée par de l'Hospital dans sa ‘2e maniere’ (voir la Lettre No. 2807), avec celle a=b2ue-2 de la pièce No. 2782, s'était aperçu de l'identité des
z de de l'Hospital avec les a de cette dernière pièce ‘ubi est e quod hinc x, et u quod hinc y. et b quod hinc a’. Or, pour la branche A∧Ω de la figure 1 de cette pièce, qui correspond avec la branche AE de la présente figure, les a étaient représentés par les ordonnées de la courbe אζ, et il était donc clair que les sommations en question devaient s'exécuter depuis la valeur z=a jusqu'à la valeur arbitraire z=a2yx-2; après quoi Huygens pouvait obtenir aisément les valeurs véritables de ces sommes en réduisant leur détermination à la quadrature bien connue des hyperboloïdes φ=a3z-2 et θ=a4z-3. -2a3dz/zz+a4dz/z3.’ On y voit comment Huygens, en comparant la substitution z=a2yx-2, employée par de l'Hospital dans sa ‘2e maniere’ (voir la Lettre No. 2807), avec celle a=b2ue-2 de la pièce No. 2782, s'était aperçu de l'identité des
z de de l'Hospital avec les a de cette dernière pièce ‘ubi est e quod hinc x, et u quod hinc y. et b quod hinc a’. Or, pour la branche A∧Ω de la figure 1 de cette pièce, qui correspond avec la branche AE de la présente figure, les a étaient représentés par les ordonnées de la courbe אζ, et il était donc clair que les sommations en question devaient s'exécuter depuis la valeur z=a jusqu'à la valeur arbitraire z=a2yx-2; après quoi Huygens pouvait obtenir aisément les valeurs véritables de ces sommes en réduisant leur détermination à la quadrature bien connue des hyperboloïdes φ=a3z-2 et θ=a4z-3.
-
voetnoot3)
- On rencontre cé ‘demeslé’ à la page 41 du Livre J. Partant de l'équation n=y:√m,
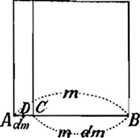
Huygens en déduit: ‘n diminutum [c'est-à-dire n-dn]==(y-dy):√m-dm=(y√m-√m dy):√mm-mdm et il ajoute: ‘Hic vero sciendum est √mm-mdm censendum aequari m-½dm, quia dm minima respectu m. Nam inter AB=m et BC=m-dm media proport. BD est quasi arithmetice media. Ideoque AD=½dm et BD=m-½dm’. Après cela, il trouve aisément dn=y/√m-y√m-√m dy/m-½dm=mdy-½ydm/m√m-½dm√m=mdy-½ydm/m√m ou, enfin, substituant mdy=½ydm+½mdm, dn=½m-½dm.
-
voetnoot4)
- Voici l'histoire de ces vains efforts, telle qu'on la démêle aisément au moyen des pages 47 et 48 du Livre J. Sous le titre: ‘Inventio Regulae Hospitalianae ad diminuendos terminos aequationum differentialium’ Huygens y commence des recherches sur la substitution x=myθ, à propos de laquelle il remarque: ‘x=myθ, ut transmutetur aequatio. θ est numerus exponens potestatis του y. Intelligendum quasi ponatur aθx=myθ ut servetur homogenea’. De cette relation x=myπ, il déduit par la méthode exposée dans la note précédente:
dm=x:yθ-(x-dx):(yθ-θ yθ-1 dy)=(-θxyθ-1 dy+yθdx):y2θ, d'où il suit: dx=yθ dm++θ myθ-1 dy.
Passant alors au cas plus général x=na yb, il trouve: dn=x1/a:yb/a-(x1/a-1/ax1/a-1dx): (yb/a-b/a yb/a-1 dy)=(-b/a x1/a yb/a-1 dy+1/ayb/a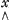 b/a-1 dx):y2b/a; relation dont il va se servir pour calculer la valeur de dx. Or, à l'endroit marqué par Huygens avec le signe ∧, il y a une faute de calcul, puisque, au lieu de xb/a-1, on doit lire x1/a-1, et en conséquence Huygens n'obtient pas le résultat attendu: dx=ana-1 yb dn+bna yb-1dy. Toutesois la présence mème du signe ∧ démontre que Huygens doit s'être aperçu plus tard de sa méprise; mais sans reprendre alors les calculs qui le fatiguaient. b/a-1 dx):y2b/a; relation dont il va se servir pour calculer la valeur de dx. Or, à l'endroit marqué par Huygens avec le signe ∧, il y a une faute de calcul, puisque, au lieu de xb/a-1, on doit lire x1/a-1, et en conséquence Huygens n'obtient pas le résultat attendu: dx=ana-1 yb dn+bna yb-1dy. Toutesois la présence mème du signe ∧ démontre que Huygens doit s'être aperçu plus tard de sa méprise; mais sans reprendre alors les calculs qui le fatiguaient.
-
voetnoot8)
- Ici Huygens nota en marge, en manière de memorandum: ‘S'il est nécessaire de soustraire l'autre suite. il n'a pas votre suite. Votre remarque est importante’.
-
voetnoot9)
- Comparez le commencement de la Lettre de Huygens à de l'Hospital datée du 5 novembre 1693.
-
voetnoot10)
- Consultez sur le même exemple la note 16 de la Lettre No. 2735.
-
voetnoot16)
- Voir l'article publié dans les ‘Acta’ de juin 1693 sous le titre: ‘Jacobi Bernoullii solutio problematis Fraterni ante octiduum Lipsiam transmissi’.
-
voetnoot17)
- Les recherches de Huygens sur le problème de Bernoulli commencent à la pag. 44 du Livre J. Sur cette page et la suivante il s'est essayé au cas particulier BD=2AD. Posant AC=x,
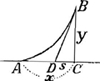
BC=y, DC=s, on a BD=√y2+s2=2AD=2x-2s, d'où Huygens déduit (écrivant par erreur 4xx-8xs-4ss pour le carré de 2x-2s): DC=s=√36/25xx-⅕yy-4/5x, après quoi la proportion s:y==dx:dy mène facilement à l'équation différentielle:
√36/25xx-⅕yy dy-4/5xdy=ydx.
Sur cette équation Huygens essaie successivement les substitutions √36/25xx-⅕yy==√am et x=ny-4/5, dont la dernière le conduit à l'équation simplifiée:
√36/25nny-8/5-⅕yy dy=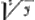 dn, à propos de laquelle il temarque: ‘hactenus rectè. Sed jam efficiendum esset ut ab altera parte aequationi tantum essent n et dn; ab altera tantum y et dy; quod difficile; alias summae non possunt colligi’. dn, à propos de laquelle il temarque: ‘hactenus rectè. Sed jam efficiendum esset ut ab altera parte aequationi tantum essent n et dn; ab altera tantum y et dy; quod difficile; alias summae non possunt colligi’.
Après avoir échoué ainsi, il attaque à la page 46 le cas plus simple AD=DB, qui doit amener le cercle. Alors il arrive, par la voie indiquée, à l'équation différentielle xxdy--yydy=2yxdx, qu'il intègre facilement 1o. par la méthode de Fatio, divisant par y2, ce qui donne, en ajoutant une constante:-x2y-1-y+a=0, ou bien x2+y2-ay=0; 2o. par la méthode de de l'Hospital, en posant y=mx2, d'où suit m-2 dm=dy.
Enfin aux pages 47 et 49 Huygens s'occupe de la description mécanique de la courbe et découvre à cette occasion le point de rebroussement qui se présente dans le cas où DB < AD et dont il sera question bientôt dans ses lettres à de l'Hospital du 1er octobre et du 5 novembre 1693.
-
voetnoot19)
- En effet, l'article de Jacques Bernoulli, cité dans la note 16, débute par la phrase suivante: ‘Elegans est hoc problema, in quod incidimus [lui et son frère] occasione Hugenianorum quorundam, quae nuperrime in Actis Roterodamensibus comparuere’.
-
voetnoot20)
- Voici cette description telle qu'on la rencontre dans l'article mentionné: ‘Deinde omnes hae
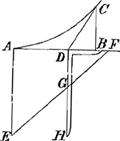
Curvae describuntur motu continuo fili GDC in alterutra extremitate C pondus annexum habentis hoc pacto: In Triangulo AFE rectangulo ad A, cujus crus AE aequale sit longitudini fili GDC, applicetur norma BDH, ea ratione ut dum crus DB super AB versus A volvitur, alterum HD fili portionem GD ante se pellendo, lateri Trianguli AE perpetuo parallelam manere, ejusque extremitatem G, super hypothenusa FE incedere cogat: sic fiet, ut pondus alteri extremitati C annexum & attractum curvam describat AC ita comparatam, ut AD sit ad portionem fili DC, tangentem scil. Curvae, in ratione data crurum Trianguli AF & AE’.
-
voetnoot21)
- Il s'agit des descriptions mentionnées dans la note 17, qui correspondent avec celles des figures 4, 5 et 6 de la Lettre à de l'Hospital du 5 novembre 1693.
-
voetnoot22)
- Elle y parut sous le titre: ‘Curvae dia-causticae, earum relatio ad evolutas, aliaque nova his affinia. Item: Natura osculorum uberius explicata. Celeritates Navium desinitae. Regulae pro Resistentiis, quas Figurae in Fluido motae patiuntur &c. par l.B. [Jacques Bernoulli].
-
voetnoot23)
- Allusion au passage suivant que l'on rencontre dans l'article cité de Jacques Bernoulli: ‘Solus Hugenius in Tractatu de Lumine schema nobis sistit integrae Dia-Causticae, sed circularis tantum & per radios incidentes parallelos genitae: Generalem vero Dia-Causticarum considerationem, earumque ad Evolutas relationem, primus, ni fallor, ego agressus sum, nec irrito spero successu, ut ex sequenti constructione liquebit....’. Les recherches de Huygens sur la diacaustique en question se trouvent aux pages 119-122 de l'édition originale du ‘Traité de la lumière’.
-
voetnoot24)
- Consultez sur cette construction, et sur le passage qui va suivre, la pièce No. 2626.
-
voetnoot25)
- Dans un article publié dans les ‘Acta’ de mai 1692 sous le titre: ‘Jac. Bernoulli mathematum professoris Basileensis Curvatura veli, in litteris Ejus d. 9 Martii hujus anni Lipsiam perscriptis communicata’.
-
voetnoot26)
- Dans l'article intitulé: ‘Generalia de natura linearum, anguloque contactus & osculi, provolutionibus, aliisque cognatis, & eorum usibus nonnullis’, qui parut dans les ‘Acta’ de septembre 1692, Leibniz, sous l'influence sans doute de la remarque de Huygens que l'on rencontre à la page 133 de la Lettre No. 2693, avait inséré la phrase suivante: ‘Eximia quaedam inesse videntur illis, quae de sigura veli a vento tensi Cl. Bernoullius nuper disseruit; tametsi de tota re (in qua non desunt scrupuli) ob molem aliorum negotiorum non expensa, pronuntiare non ausim’. En réponse, Jacques Bernoulli, dans l'article cité dans la note 21, l'invita à exposer les raisons de ses doutes, puisque ‘nec Frater meus....nec ipse illustris Hospitalius, quicum ille inventum communicaverat, quicquam in illo fallaciae deprehenderunt’.
-
voetnoot27)
- Consultez à ce sujet l'Appendice Il de la Lettre de Huygens à de l'Hospital du 5 novembre 1693.
-
voetnoot28)
- C'est-à-dire dans le Recueil publié par de la Hire et mentionné dans la note 3 de la Lettre No. 2816. Voir la page 336 de cet ouvrage.
-
voetnoot30)
- Voir la pièce No. 1891. Dans les deux solutions l'hyperbole qui, par ses intersections avec le cercle donné, fait connaître les points de réflexion, est la même, mais sa construction telle qu'elle est donnée dans la pièce No. 1891, est la plus simple et la plus élégante. Ajoutons que la solution antérieure donnée dans la pièce No. 1745 diffère également de celle que l'on trouve dans le Recueil publié par de la Hire.
-
voetnoot31)
- Voir l'ouvrage cité dans la Lettre No. 2616, note 8, où l'on trouve en effet, à la page 492, cette construction formulée à peu près de la même manière qu'à la page 189 de la pièce No. 1891. Toutefois dans l'article, qui occupe les pages 483-495 de l'ouvrage d'Ozanam, Huygens n'est pas
nommé, ce qui est d'autant plus remarquable que l'auteur, à propos d'une déduction de l'équation du quatrième degré qui fait connaître les points de réflexion, y cite ‘M. l'Abbé de Catelau, dont le mérite est connu de tous les Sçavans’, ce qui nous semble rendre suspect l'oubli de l'auteur.
|