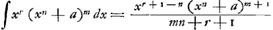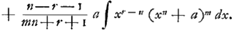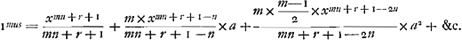No 2812.
David Gregory à Christiaan Huygens.
[juin ou juillet 1693].
Appendice II au No. 2810.
La pièce se trouve à Leiden, coll. HuygensGa naar voetnoot1).
| 1. | Nota esse semper 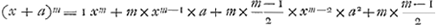 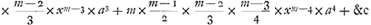 . . |
| 2. | Ergo si sit l applicata et x abscissa curvae, et b, c et a quantitates notae, r, n et m exponentes indeterminati, atque aequatio data l=xr×(xn+a)m, tum etiam 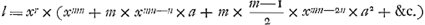 . . |
| 3. | Sive ducendo terminos seriei singulos in xr eritGa naar einda) 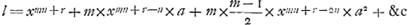 . . |
| 4. | Et juxta CanonemGa naar eindb) Gregorianum addendo cuique exponenti unitatem et dividendo quemque terminum per exponentem ita auctumGa naar eindc) erit
Area 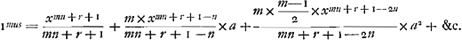 |
|
| 5. | Jam si haec area dividatur per hanc quantitatem (xn+a)m+1 debet esse aequalis etiam areaeGa naar voetnoot2). |
| 6. | Atqui (xn+a)m+1 reducta in seriem aequalis est xmn+n+(m+1)×xmn × ×a+&c. |
| |
|
Ubi nota quemque terminum duci intelligitur in (xn+a)m+1Ga naar voetnoot4). |
| 14. | Patet verò etiamGa naar eindf) hanc seriem semper abrumpi cum r+1=n, vel=2n, vel=3n, five r+1/n aequatur numero integro et positivo, et tum quadraturam curvae definitam exhibere. |
| 15. | Et simili modi si aequatio sit l=bxr×(sx+a)m, series Aream exhibens |
| 16. | Erit 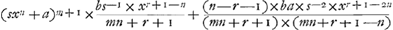 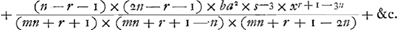
Ubi nota unumquemque terminum duci intelligitur in (sxn+a)m+1. |
|
-
voetnoot1)
- La pièce est probablement de la main de David Gregory. Nous avons remplacé, dans l'imprimé, la notation:
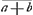 du manuscrit par (a+b). Les notes a), b) etc. contiennent les annotations inscrites sur le manuscrit par Huygens. du manuscrit par (a+b). Les notes a), b) etc. contiennent les annotations inscrites sur le manuscrit par Huygens.
-
einda)
- delenda hic quibus supposui puncta. non enim ducuntur termini precedentes in xr, sed pro (xr)×xmn scribitur xmn+r in singulis [Christiaan Huygens]. Nous avons imprimé en italiques les mots que Huygens marque par des points].
-
eindb)
- Au dessus du mot Canonem Huygens écrivit: Lemma.
-
eindc)
- Vide pag. 6 Exercit. de dimensione sig. geom. Dav. Gregorii [Christiaan Huygens]Ga naar voetnoot5).
-
voetnoot5)
- Voici le ‘Lemma’ tel qu'on le rencontre à la page citée de l'ouvrage de David Gregory mentionné dans la note 6 de la pièce No. 1709:
‘Quâvis rectâ in partes innumeras discerptà, summa quarumvis dignitatum, ab innumeris istis rectis ab extremitate propositae rectae continuó incipientibus, genitarum, equalis est rectae propositae potestati, quaesitis potestatibus proximè superiori, divisae per suum exponentem’.
Ajoutons que l'on trouve, à propos de ce ‘lemma’, à la page 6 du livre J des Adversaria, la remarque suivante de Huygens: ‘Hoc apud Geometras demonstratum dicitur. Sed videtur non tam universaliter demonstratum ut etiam Radices, quadrata, cubica, etc. pro potestatibus habeantur; quanquam per consequentias ostendatur verum esse postquam de veris potestatibus demonstratum fuerit’.
-
voetnoot2)
- C'est-à-dire: après avoir multiplié le quotient obtenu par ce même facteur. Comparez l'article 12.
-
voetnoot3)
- Remplacez les mots qui suivent par ‘xmn+n seriei dat pro Quotiente’.
-
einde)
- hoc apposui [Christiaan Huygens], c'est-à-dire: a.
-
voetnoot4)
- Comme on le voit, cette démonstration de la règle de Gregory exposée dans la note 19 de la Lettre No. 2810, est incomplète, puisqu'elle s'arrête au deuxième terme, tandis que les embarras du calcul s'accroissent pour les termes suivants. Toutefois la règle est correcte, sauf l'addition nécessaire d'un terme constant, et on y arrive facilement par l'application répétée de la formule:
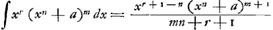 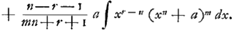
-
eindf)
- hoc erat delendum [Christiaan Huygens].
|
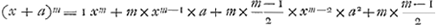
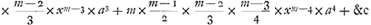 .
.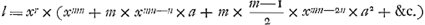 .
.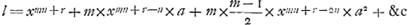 .
.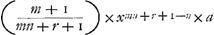 qui subtractus a secundo termino Areae notatae hic 1mus nempe subtractus ab m×xmn+r+1-n/mn+r+1-n dat
qui subtractus a secundo termino Areae notatae hic 1mus nempe subtractus ab m×xmn+r+1-n/mn+r+1-n dat
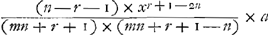 .
.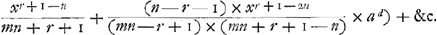
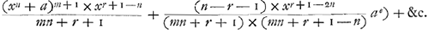 Ga naar einde)
Ga naar einde)
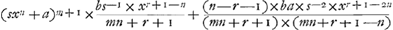
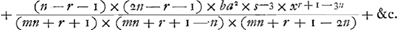
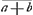 du manuscrit par (a+b). Les notes a), b) etc. contiennent les annotations inscrites sur le manuscrit par Huygens.
du manuscrit par (a+b). Les notes a), b) etc. contiennent les annotations inscrites sur le manuscrit par Huygens.