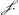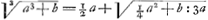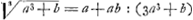BE et qu'alors la quantitè de 2axx/3y-x4/2yy est la vraie valeur de l'espace AEBGa naar voetnoot6).
Il resteroit à rendre raison pourquoy ce n'est pas celle de l'espace ACB. Cependant je trouve ces deux manieres extremement belles, et je crois que la troisieme le sera pour le moins autant.
Je m'estois embarassè en cherchant la courbe qui a pour soutangente x- y, mais je l'ay trouvée depuis et je vois que cette courbe est une partie de la continuation de la vostre Ga naar voetnoot7) dont la soutangente estoit x+ y; et qu'en posant la proprietè de cette courbe telle en general, que DE partie de l'axe interceptée entre la tangente
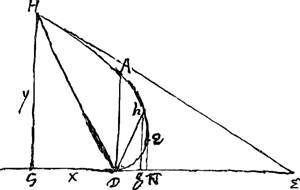
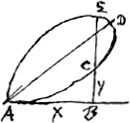
et le commencement D, soit egale à l'appliquée HG; Toute la courbe alors est HAQD. dont la partie DQ jusqu'à la tangente QN perpend. re sur GD, a ses soutangentes x- y, qui sont y- x dans la partie QA, depuis Q jusqu'à la perpend. re DA.
J'ai aussi trouvèGa naar voetnoot8), en posant DA ∞ a, DG ∞ x, GH ∞ y, que l'espace ADGH est ½xy+¼yy-¼aa, et non pas comme il vient par vostre calcul, ½xy+¼yy, ce que vous reconnaitrez avec un peu d'attention. Mais la mesure generale des segmens DQH, DQh est remarquable, qui sont tousjours egaux à ¼yy, c'est a dire au quart du quarrè de la perpendiculaire qui fait leur hauteur sur DG.
Pour les autres difficultez que je vous avois proposees, Monsieur, j'attendray, s'il vous plait vos solutions, pour ne pas consumer trop de temps à les applanir
| |
Item qui est autheur du Traitè de la manoeuvre des vaisseauxGa naar voetnoot17) dont j'aurai l'honneur de vous parler une autre foisGa naar voetnoot18). Je suis avec respect etc. |
-
voetnoot1)
- Chr. Hugenii etc. Exercitationes Mathematicae, Fasc. I, p. 275.
-
voetnoot2)
- Ce sommaire est emprunté à la page 35 du livre J.
-
voetnoot3)
- Il s'agit des trois manières de carrer le folium de Descartes, mentionnées par de l'Hospital dans la Lettre No. 2807.
-
voetnoot4)
- Voir, pour l'équation du folium rapportée aux axes BC et CM, la note 17 de la Lettre No. 2810.
-
voetnoot5)
- Comme on le sait par la Lettre No. 2810, la difficulté éprouvée par Huygens consistait dans la ‘collection de la somme’ des (ay2dx-2axydy):6x2. Or, à la page 27 du livre J, on rencontre à ce propos sous la date: ‘28 Jul. 93 Hofw.’, la remarque suivante: ‘haec supplevi ex universali ipsius methodo diminuendi numeri terminorum; nam ut in unam redigatur
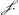 ayydx/6xx et- ayydx/6xx et- 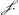 2axydy/6xx, pono ex ipsius Regula, quam ex exemplis subodoratus sum, x=my2; quia video haberi hic ydx-2xdy, ducta licet in ay/6xx. Hinc vero sicut pag. 25 et 20, [voir la note 3 de la Lettre No. 2810] sit dx=yydm+2mydy. Ita pro summis duabus istis invenitur 2axydy/6xx, pono ex ipsius Regula, quam ex exemplis subodoratus sum, x=my2; quia video haberi hic ydx-2xdy, ducta licet in ay/6xx. Hinc vero sicut pag. 25 et 20, [voir la note 3 de la Lettre No. 2810] sit dx=yydm+2mydy. Ita pro summis duabus istis invenitur 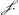 adm/6mm, quae per regulam
gener.m pag. 21 [voir la pièce No. 2811], est-a/6m, et substituendo pro m ejus valorem 6x/yy [sic] fit-ayy/6x.’ adm/6mm, quae per regulam
gener.m pag. 21 [voir la pièce No. 2811], est-a/6m, et substituendo pro m ejus valorem 6x/yy [sic] fit-ayy/6x.’
-
voetnoot8)
- Consultez, sur la manière curieuse dont les quadratures qui suivent ont été obtenues, l'Appendice No. 2814 à cette lettre, où l'on verra comment Huygens se rend de plus en plus familières les notations du calcul infinitésimal, tout en persistant d'en accompagner l'emploi par des considérations géométriques.
-
voetnoot9)
- Il s'agit de l'article de Jean Bernoulli cité dans la note 4 de la Lettre No. 2807, qui commence par la phrase suivante: ‘Prima mea hujus problematis solutio, quae reperitur tecto nomine in Diario Gallico 34. anni elapsi, non minus quam Fratris, qui suam mihi tunc temporis Parisiis commoranti transmiserat, supponit quadraturam spatii hyperbolici; id quod constructionem in praxi impossibilem reddit’, après quoi l'auteur fait suivre une seconde solution du problème, identique à peu près avec celle exposée en second lieu par de l'Hospital dans sa Lettre No. 2787, à la page 393.
Or, l'article cité du ‘Diarium Gallicum 34’ n'était autre que celui mentionné dans la note 2 de la Lettre No. 2787, publié par de l'Hospital sous le pseudonyme G***.
Cousultez d'ailleurs sur cet incident la Lettre No. 2815.
-
voetnoot10)
- Allusion au passage suivant du même article de Jean Bernoulli: ‘Curva autem ipsa AI [la courbe de de Beaune] est ex earum numero, quarum rectificationes quidem in abstracto non habentur, longitudines tamen per ipsasmet curvas construi et determinari possunt, quod Nob. Hugenius praestitit in nova sua Logarithmica, & ego jam olim in Logarithmica vulgari’.
-
voetnoot12)
- Thomas Fantet de Lagny, né à Lyon le 7 novembre 1660. Il quitta le barreau pour se vouer aux sciences. Il fut élu membre de l'Académie des Sciences en 1696, devint associé géomètre le 28 janvier 1699, associé mécanicien en mars 1699, en remplacement de Sauveur, pensionnaire surnuméraire le 8 juillet 1719 et pensionnaire géomètre le 3 février 1723, en remplacement de Varignon, enfin pensionnaire vétéran le 4 mars 1733. Après avoir professé l'hydrographie à Rochefort, il fut nommé en 1716 sous-directeur de la banque générale. Il fut encore l'un des conservateurs de la bibliothèque du Roi et membre de la Société Royale de Londres. On a de lui plusieurs ouvrages d'arithmétique, d'algèbre et de géométrie. Il mourut à Paris, le 11 avril 1734.
-
voetnoot13)
- Il s'agit de l'ouvrage intitulé:
‘Méthode nouvelle infiniment generale et infiniment abregée pour l'extraction des Racines quarrées, cubiques, &c., & pour l'approximation des mesmes Racines à l'infini dans toutes sortes d'égalitez. Proposée à examiner aux mathématiciens de l'Europe. Par M. de Lagny. A Paris de l'imprimerie d'Antoine Lambin, ruë S. Jacques, au Miroir, mdcxci. Avec permission. in-4o’, six pages plus le feuillet du titre.
En outre De Lagny publia un essai de sa méthode dans le Journal des Sçavans du 14 May 1691 sous le titre: ‘Nouvelle méthode de Mr. T.F. de Lagny pour l'approximation des Racines cubiques’.
D'après cet essai la méthode qui avait attiré l'attention de Huygens consistait pour le cas des racines cubiques dans l'application des deux formules approximatives suivantes:
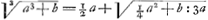
;
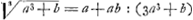
:(3a3+b), et, en effet, les valeurs calculées par ces formules ne diffèrent, en première approximation, des valeurs véritables de la racine cubique que par les valeurs+b3:81a8 et-2b3:81a8.
-
voetnoot14)
- Dans le Journal des Sçavans du 18 janvier 1694 Jean Bernoulli mentionne ‘un petit écrit’ de M. Rolle contre M. de Lagny. Cet écrit semble être devenu de nos jours très rare. D'ailleurs, dans le numéro de Janvier 1692 des ‘Mémoires de Mathématique et de Physique. Tirez des Registres de l'Académie Royale des Sciences’ (voir la note 9 de la Lettre No. 2748), Rolle, sans mentionner de Lagny, avait donné sous le titre: ‘Règles pour l'Approximation des racines des cubes irrationnels’ des règles analogues mais nullement préférables à la seconde formule de de Lagny.
-
voetnoot15)
- Consultez, sur cet ouvrage de l'abbé de Catelan et sur la polémique dont il est question ici, la note 3 du No. 2259, à laquelle nous ajoutons ici:
1o. que l'ouvrage sortait de l'imprimerie de Lambert Roulland (et non pas de Charles Robersta l) et qu'il était composé de deux morceaux bien distincts, dont le second, sur lequel la critique de de l'Hospital était surtout dirigée, portait le titre: ‘Principe de la science generale des Lignes courbes ou un des principaux elemens de la geometrie universelle’, à Paris, de l'imprimerie de Lambert Roulland, rue S. Jacques aux armes de la Reyne, mdcxci.
2o. que de l'Hospital publia encore, dans le cours de cette polémique, deux lettres publiques, l'une en Janvier, l'autre en Novembre ou Décembre 1692, qui semblent être devenues extrêmement rares.
3e que Huygens avait attribué le livre à Prestet, comme cela résulte de l'annotation suivante, qu'on trouve vers la fin du Livre H: ‘Logistique pour la science generale des lignes courbes. 1691. Je le crois de Prestet. Il traite de trouver les Tangentes des Courbes’.
4o. qu'il est curieux de remarquer comment Catelan à cette occasion se servit d'un procédé analogue à ceux signalés dans la note 1 de la Lettre No. 2260, dans les Lettres No. 2262, 2264, 2265 et la note 1 de la Lettre No. 2280, supprimant, après avoir pris connaissance de la première critique de De l'Hospital, dans les exemplaires qui lui restaient, les pages qui y avaient donné prise et les remplaçant par d'autres sans en avertir le lecteur.
-
voetnoot16)
- Voir, pour la réponse de De l'Hospital sur les deux questions contenues dans cette phrase, sa lettre du 21 octobre 1693.
-
voetnoot17)
- L'ouvrage anonyme du chevalier Renau, Ingénieur général de la Marine, portait le titre: ‘De la Theorie de la manoeuvre des vaisseaux. A Paris, chez Estienne Michallet premier imprimeur du Roy, ruë S. Jacques, à l'Image S. Paul. m.dc.lxxxix. De l'exprès commandement de sa Majesté’. in-8o. Sur une des dernières pages du Livre H, Huygens annota à propos de cet ouvrage: ‘il y a de l'algèbre, et l'autheur parait bon géomètre, mais il se trompe dans les premiers principes, ce qui rend toute sa théorie fausse’.
-
voetnoot18)
- Voir la Lettre à de l'Hospital du 5 novembre 1693.
|



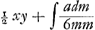 c'est-à-dire ½ xy-ayy/6x
c'est-à-dire ½ xy-ayy/6x