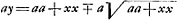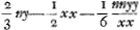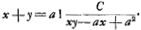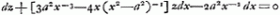Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–
[pagina 446]
| |
No 2805.
| |
[pagina 447]
| |
2e. question. On demande la courbe qui a pour soutangente 2x+x3/yy cette question se resout de la mesme maniere que la precedente. 3e. question. Il faut trouuer la courbe qui a pour equation differentielle aaxdy=3aaydx-2xyydx+2xxydy, ou divisant par aa, afin de donner vne forme conuenable, xdy=3ydx-2xyydx+2xxydy/aaGa naar voetnoot4). Je suppose y=mx3, pour reduire les deux termes xdy et 3ydx en vn seul, et j'ay dy=3mxxdx+x3 dm ce qui donne, en substituant ces deux valeurs, 3mx3dx+x4dm=3mx3dx-2mmx7dx+6mmx7dx+2mx8dm/aaGa naar voetnoot5), qui se reduit à mdx=-½xdm++aadm/4mx3, et ainsi l'equation proposée, qui etoit de quatre termes se trouue reduite à vne de trois sur laquelle j'applique de nouueau la regle en supposant x=nm-½ et partant dx=-½nm-3/2dm+m-½dn, ce qui donne par la substitution 4n3dn=aadm, et prenant les sommes n4=aam ou bien en aiouttant ou retranchant vne quantité constante, n4=aam∓a, substituant enfin dans ces deux dernieres equations à la place de n et de m leurs valeurs xm½ et yx-3, on trouve xy=aa, et yyx-aay∓x3=0, qui sont les equations qui expriment la nature des courbes cherchées. Jl arriue quelque fois que l'equation differentielle ne peut estre reduite à vn moindre nombre de termes par cette regle, soit parce qu'elle n'a pas vne forme conuenable, soit parce qu'en diminuant le nombre des termes d'vn coté on l'augmente de l'autre, de sorte qu'on n'est pas plus auancé qu'auparauant. Il faut auoir recours alors à quelque adresse particuliere ce qui se comprendra mieux par un exemple. Soit proposée l'equation differentielleGa naar voetnoot6) axydx+aaxdx+x3dx==a3dy+axxdyGa naar eindb). Si l'on diuisoit par ax, on pouroit reduire les termes ydx et xdy en vn seul, mais parce que la mesme supposition augmente d'vn terme les autres, je prends plusieurs termes pour vn seul en supposant aa+xx=am, ce | |
[pagina 448]
| |
qui change l'equation en celle-ci mdy=½ydm+½mdm qui n'a que trois termes, et sur laqu'elle s'applique la regle en supposant y=nm½ ce qui la reduit a dn=½m-½dm, dont les sommes sont n=m½ ou n=m½∓a, substituant enfin a la place de n et de m leurs valeurs ym-½ et aa+xx/a je trouue ay=aa+xx et  , d'ou je connois que la courbe peut estre vne parabole ou vne ligne plus composée. Cette regle peut aussi seruir lorsque les courbes sont mecaniques. Soit proposée par exemple de decrire la courbe qui a pour soutangente x+y. L'equation differentielle sera ydx=xdy+ydy, et supposant x=myGa naar voetnoot7), on aura, apres les substitutions faites, ady=ydm, qui est vne equation a la logarithmique, d'ou l'on tire cette constructionGa naar eindc). , d'ou je connois que la courbe peut estre vne parabole ou vne ligne plus composée. Cette regle peut aussi seruir lorsque les courbes sont mecaniques. Soit proposée par exemple de decrire la courbe qui a pour soutangente x+y. L'equation differentielle sera ydx=xdy+ydy, et supposant x=myGa naar voetnoot7), on aura, apres les substitutions faites, ady=ydm, qui est vne equation a la logarithmique, d'ou l'on tire cette constructionGa naar eindc).
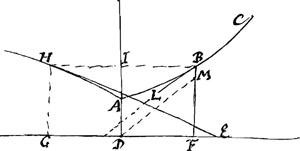 Soit vne logarithmique quelconque ABC qui a pour asymptote la droite DF sur la qu'elle soit abbaissée librement la perpendiculaire indefinie DAI, qui rencontre la logarithmique au point A, soit mené DM parallele à vne tangente quelconque BL et qui coupe en M l'ordonnée BF qui part du point touchant B, et ayant pris DG=FM, soit acheué le rectangle FH, je dis que le point H sera à la courbe requiseGa naar voetnoot8). Car ayant mené la touchante HE on aura DE=GH. Pour auoir la quadrature de cette courbe ydx=xdy+ydy, on aioustera de part et d'autre ydx et on aura 2ydx=xdy+ydx+ydy, d'ou il suit que la somme des 2ydx, c'est a dire le double de l'espace ADGHGa naar voetnoot9)=xy+½yyGa naar eindd). | |
[pagina 449]
| |
On demande la courbe qui a pour soutangente yy-xy/a, qui est celle de Mr. de Beaune. L'equation differentielle sera adx=ydy-xdy, et supposant y-x=z, on trouue apres les substitutions faites adx=azdz/a-z, d'ou l'on voit que la courbe
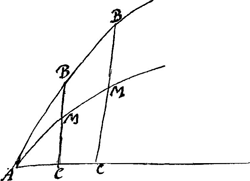 AMM dont les appliquées MC sont exprimées par z, et les coupées AC par x, depend de la quadrature de l'hyperbole, mais comme on a supposé y=z+x, il faut prolonger CM en B, en sorte que MB=AC, et le point B sera à la courbe cherchéeGa naar voetnoot10). Je reserue à la 1re fois à vous enuoyer la rectification d'vne portion quelconque de cette courbeGa naar voetnoot11) qui est assurement plus difficile que celle de la logarithmique comme vous l'eprouuerez, si vous vous donnez la peine d'y penser. Vous me ferez plaisir de me faire part des regles que vous auez pour l'inuerse des tangentes. Au reste je n'ay pû resoudre vos deux courbes et il y a apparence qu'elles se reduisent à des quadratures fort composéesGa naar voetnoot12), si vous en sauez la resolution, mandez le moi et ie m'y appliquerai avec plus de soin. | |
[pagina 450]
| |
J'ai ensin trouué vn horlogeur appellé l'anglois qui demeure à la place Dauphine, et qui est le seul que ie scache qui fasse des montres de l'inuention de Mr. Hautefeüille, quoi qu'elle ne merite en nulle maniere le nom d'inuention puis qu'elle ne consiste qu'à faire les balanciers pleins, mettre le ressort spiral au dessus qui est plus fort qu'à l'ordinaire et qui fait plus de tours, et de faire des palettes au balancier plus grandes, tout cela parce que le balancier est beaucoup plus pesant. Jl pretend que l'air qui entre dans les balanciers creux doit oster quelque chose de leur justesse, et d'ailleurs que plus le balancier est pesant, plus la montre ira iuste. Je vous laisse à penser si cela merite le nom d'inuention, pour moi j'estime beaucoup plus nos montres ordinaires à grand balancier, et i'ai mesme fait auouer à cet horlogeur que ces montres n'iroient pas plus iuste que les autres. Jl me paroit qu'elles seront suiettes à vn grand inconuenient qui est que la pesanteur du balancier poura faire elargir les trous de la platine dans lesquels entre son piuot ce qui osteroit toute la justesse. Je vous prie de ne me point nommer car l'horlogeur m'a fait vn grand mystere de tout ceci, et m'a fort prié de n'en point parler, cependant la chose ne peut estre longtemps secrette, puis qu'il uendra, selon les apparences, incessamment de ces sortes de montres. Je ne vous puis faire de reponce sur le suiet de Mr. le Duc de Roanez car il est à la campagne depuis quelque temps, et ie ne manquerai pas à son retour de lui dire ce que vous me mandezGa naar voetnoot11). La longueur de cette lettre m'empesche de vous entretenir sur la baguette, plusieurs de nos philosophes se sont empressez d'en rendre raison sans beaucoup aprofondir la uerité du fait, je crois qu'il en sera comme de la dent d'or d'allemagne. Je suis tres veritablement
Monsieur
Vôtre tres humble et tres obeissant seruiteur le M. de l'Hospital.
A Paris ce 12e mai.
Nous n'auons point ici les liurets du Sieur de beauval depuis la guerre ainsi vous me ferez plaisir Monsieur de m'enuoyer les feuilles que vous me marquez. |
|


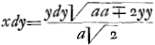 dont la somme
dont la somme 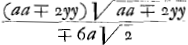 donne la quadrature du complement de l'espace curuiligne
donne la quadrature du complement de l'espace curuiligne