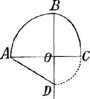
Quapropter facile per methodum Slusii tangens et subnormalis OD inquiritur, quae cum aequalis sit OC, expuncto ζζ aequationem subministrat ad curvam BC velut requirebatur.
Subnormalis ∞ a3-½bζζ/bb+byGa naar voetnoot3) ∞ x unde a3-½bζζ ∞ bbx+byx vel quia ζζ ∞ 2a3y/bb+by:a3-a3by/bb+by ∞ bbx+byx, factaq. reductione, omnibusque divisis per bb:a3 ∞ bbx+2byx+yyx.
Ita m.p.9.Ga naar voetnoot4) loco y3+ayψ etc.Ga naar voetnoot5) scribo aψ ∞ ay3/-ay+bψ-ψ2 ∞ ζζ/2 unde 2ay3∞-ayζζ+bψζζ-ψ2ζζ et ad tangentem inquirendam 6ay2t+atζζ∞ ∞ 2bψζζ-2ayζζ-2ψ2ζζGa naar voetnoot6); t ∞ subtangenti posito subnormalis itaq. OD erit 6ay2+aζζ/2bψ-2ay-2ψ2 vel quia ζζ ∞ 2aψ. 3ay2+aaψ ∞ bψx-ayx-ψ2xGa naar eindb). |
-
voetnoot1)
- Cette pièce contient des remarques de Steigerthal à propos de l'ouvrage de Hubertus Huighens, intitulé: ‘Adversiones quaedam circa proportionem quam ad rectilineas habent figurae curvilineae’ et dont il est question dans la note 1 de la Lettre No. 2730. Elle doit avoir été accompagnée d'une lettre de Steigerthal, qui nous manque, et qui a été reçue par Huygens le 15 mai 1693, comme il paraît si l'on combine la réponse de Huygens avec une annotation que l'on rencontre sous cette date dans le livre J des Adversaria et qui commence par la phrase: ‘D. Alberti medecin de l'Electeur de Hannover m'apporta des lettres de Mr. Steigerthal, de Venise’.
-
einda)
- Steigerthalii [Christiaan Huygens].
-
voetnoot2)
- Cette première remarque de Steigerthal se rapporte à l'exemple 1 de Hubertus Huighens, que l'on trouve dans la note 2 de la Lettre No. 2735. Pour le montrer, il suffira de rappeler que dans la note citée la notation de Christiaan Huygens a été suivie. Ainsi, pour se conformer à celle de Hubertus, employée ici par Steigerthal, on doit remplacer respectivement les x et z de la note par y et x.
Le problème, résolu ici par Steigerthal, consiste donc à trouver la courbe OBC dont l'aire est exprimée par aψ=a3y:(b2+by). A cet effet, il commence par construire la courbe AB, pour laquelle ½AO2=½ζ2=aψ=a3y:(b2+by); puis il calcule la sousnormale de cette courbe, qui, d'après le théorème de Barrow, sur lequel on peut consulter la note 8 de la Lettre No. 2721, doit être égale à l'ordonnée OC=x de la courbe cherchée. Comme on le voit, sa méthode est identique avec celle de Huygens, exposée dans le § I de la pièce No. 2736.
-
voetnoot3)
- La sousnormale OD=ζdζ/dy s'obtient facilement sous cette forme par la différentiation de l'équation b2ζ2+byζ2-2a3y=0 de la courbe BA.
-
voetnoot4)
- Comparez, sur ce qui va suivre et qui constitue la seconde remarque de Steigerthal, la pièce No. 2737, qui contient les remarques de Huygens sur la même page 9 du livre de Hubertus Huighens.
-
voetnoot5)
- C'est-à-dire y3+ayψ=bψψ-ψ3. Voir le commencement de la pièce citée dans la note précédente.
-
voetnoot6)
- Formule fautive. Steigerthal doit l'avoir obtenue par un procédé quelconque revenant à différentier l'équation qui précède, et à remplacer ensuite ζ dy/dζ par t; mais, ce faisant, il a traité ψ comme une constante, tandis qu'il est clair qu'il aurait dû introduire dψ=xdy:a, auquel cas il aurait obtenu
l'équation finale de la présente pièce sous la forme correcte: 3ay2+ayx=-aaψ+2bxψ-3xψψ, trouvée par Hubertus Huighens, et déduite à sa manière par Christiaan Huygens dans la pièce No. 2737.
-
eindb)
- dicebatGa naar voetnoot7) hunc calculum suum non in omnibus consentire cum eo quem tradit Huyghenius ZelandusGa naar voetnoot8) [Christiaan Huygens].
-
voetnoot7)
- Dans la Lettre que nous ne connaissons pas et qui doit avoir accompagné la présente pièce.
-
voetnoot8)
- C'était, on le voit par la note 6, la faute de Steigerthal, comme Huygens le supposait dans sa réponse du 19 novembre 1693.
|