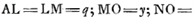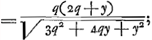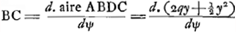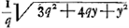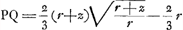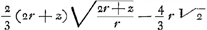poterunt per libelli mei bibliopolamGa naar voetnoot3), cujus nomen, et locum domicilii pagina tituli indicabit:
sed vereor, ne nimium abutar humanitate vestra, quare aliud nihil hic addam, quam quod velis illius rei culpam adscribere desiderio, quo teneor, videndi, ut per te, Vir nobilissime, ultima manus imponatur rei tam diu frustra quaesitae. Vale.
dabam Medioburgi
20 Januarii 1692.
Ed: gestr: welgebore Heer
d'heer Christiaen Huighens,
wonende op het pleyn
In den Haagh.
franco.

|
-
voetnoot1)
- Aux renseignements que Hubertus, ou Hubrecht, Huighens a fourni sur lui-même dans sa lettre à Christiaan du 3 mars 1692, nous pouvons ajouter encore ceux que nous devons à l'obligeance de M.H.A. van Doorn, bourgmestre de Veere, savoir, que le 13 novembre 1676, notre Hubertus, natif de Liefkenshoek en Flandre, a été admis, à l'âge de 25 ans, comme citoyen (‘poorter en burger’) de Veere, où on le rencontre en 1692, pour la première fois, sur la liste des échevins de cette ville. Il y manque en 1703, pour reparaître en 1704. Il mourut en 1705.
Pour autant que nous sachions, il n'a écrit que deux petits ouvrages, rédigés en Latin. Le premier, les ‘Adversiones quaedam circa proportionem quam ad rectilineas habent figurae curvilineae’ (1692?), dont il sera question dans la correspondance entre Christiaan et lui, semble absolument perdu, puisque, malgré tous nos efforts, il nous a été impossible d'en retrouver un exemplaire.
Du second, qui porte le titre: Methodus Inveniendi Longitudinem Linearum Curvarum, nec non Aream Figurarum Curvilinearum, Lectori Examinanda Proposita. Per Hubertum Huigenium. Medioburgi, Ex Officina Aroni à Poulle, 1700. (19 pages, avec planche), le British Museum possède un seul exemplaire, dont la Société Hollandaise des Sciences de Haarlem a fait prendre copie à cette occasion.
Dans ce second ouvrage, Hubertus Huighens prétend, sous quelque réserve comme nous le verrons, avoir accompli la quadrature du cercle et de l'hyperbole. Pour donner un aperçu de cet écrit étrange et de la personnalité scientisique de son auteur, nous suivrons Hubertus dans les chemins détournés qui l'ont mené, comme il le croit, à la quadrature de cette dernière courbe.
Pour commencer donc, il pose, dans la figure 1, qui représente une hyperbole équilatère:
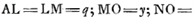 . .
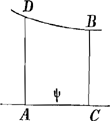
Ensuite il construit une figure ADBC (fig. 2) telle que BC=
aire ADBC=2qy+½y2. Il ne motive pas expressément le choix de ces valeurs; mais il dit qu'alors la base AC de cette figure sera égale à ψ; ce qui est vrai puisque la relation 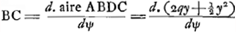 , où , où
dψ=1/q. d. aire MPNO=1/q. NO.dy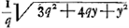 . dy, est vérifiée par cette valeur de BC, et qu'en outre l'aire ADBC=2qy+½y2 et AC=ψ s'annulent simultanément, pour la valeur y=0. . dy, est vérifiée par cette valeur de BC, et qu'en outre l'aire ADBC=2qy+½y2 et AC=ψ s'annulent simultanément, pour la valeur y=0.
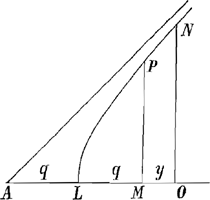
Cependant Hubertus n'emploie cette figure ADBC que comme une figure auxiliaire devant servir à démontrer que si, dans la figure 3, on a:
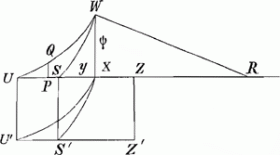
arc. SW=1/q (2qy+½y2) et SX=y, alors WX=ψ; à cet effet, il applique un théorème de Heuraet que l'on rencontre dans l'ouvrage cité dans la Lettre No. 587, note 5, et qui fait dépendre la rectification d'une courbe donnée de la quadrature d'une aire courbe devenant, dans ce cas-ci, identique avec l'aire ADBC de la figure 2.
Jusqu'ici tout va bien, mais maintenant l'auteur introduit un théorème d'après lequel, si deux courbes comme SW et UW sont convexes toutes les deux vers SX et qu'elles ont une tangente commune en W, alors Arc. UW serait égal à US+Arc. SW. Le raisonnement qu'il emploie pour établir ce faux théorème est difficile à suivre, mais il semble vouloir soutenir, qu'il doit être possible de désormer un rectangle comme USZZ′S′U′ de telle manière qu'il prenne, en conservant la longueur du côté UZ, tour à tour les figures UWXU′ et USWXS′U′. Toutefois il ajoute: ‘Quamvis res illa per se nota mihi videatur, tamen a lectore peto ut illam accuratè examinare velit, nam non solum in Philosophia, sed etiam in mathesi circa prima principia facile errari potest.’
Pour utiliser ce théorème il pose UP=z, 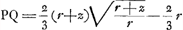 . Alors la courbe UQW est une courbe rectifiable et il trouve pour la longueur de l'arc UW la valeur exacte: . Alors la courbe UQW est une courbe rectifiable et il trouve pour la longueur de l'arc UW la valeur exacte: 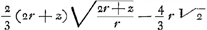 . Calculant alors, pour UX=z, la valeur XR de la sousnormale de cette courbe, il la pose égale à celle de la sousnormale de l'autre courbe SW au point W. De même il égale les valeurs de WX pour les deux courbes. Appliquant ensuite le faux théorème mentionné, il a obtenu, entre les quantités y, ψ, q, z, et r, trois équations et il suffit d'en éliminer z et r pour avoir la quadrature cherchée. . Calculant alors, pour UX=z, la valeur XR de la sousnormale de cette courbe, il la pose égale à celle de la sousnormale de l'autre courbe SW au point W. De même il égale les valeurs de WX pour les deux courbes. Appliquant ensuite le faux théorème mentionné, il a obtenu, entre les quantités y, ψ, q, z, et r, trois équations et il suffit d'en éliminer z et r pour avoir la quadrature cherchée.
Ayant trouvé par le même principe, mais à l'aide de formules encore plus compliquées, la quadrature du cercle, Hnbertus ajoute naïvement: ‘Eodem modo, quae hic inventa est circuli, et hyperbolae quadratura, inveniri quoque potest cujuscunque curvae lineae longitudo, et cujuscunque Figurae curvilineae area, ita ut, si verum inveniatur, quod rectangulum.....[UZZ′U′] flecti, et mutari potest in Figuram curvilineam.....[UWXU′], praeter calculi laborem non majorem difficultatem inveniet lector in quaerenda unius, quam alterius, curvae lineae longitudine, necnon in quaerenda unius, quam alterius Figurae curvilineae area.’
Si d'ailleurs nous nous sommes étendus un peu longuement sur ce travail de Hubertus, c'était parce que sa correspondance avec Christiaan Huygens et les termes, dans lesquels celui-ci le mentionne dans ses lettres, nous semblaient propres à exciter quelque curiosité à l'égard de ce mathématicien entièrement inconnu, qui possédait, comme on l'aura vu, une certaine habileté, alors peu commune, dans le maniement de la nouvelle analyse, mais qui n'était, toutefois, qu'un esprit faux dont l'oeuvre ne peut avoir eu de valeur réelle.
-
voetnoot2)
- Chr. Hugenii etc. Exercitationes Mathematicae, Fasc. II, p. 136.
-
voetnoot3)
- Probablement Aronus à Poulle, l'éditeur de la ‘Methodus’.
|