Fig. 3.
| y+x:y=dx:dy |
| ydx=xdy+ydy |
| ydx-xdy=ydy |
 Ga naar voetnoot10)Ga naar voetnoot11)
Ga naar voetnoot10)Ga naar voetnoot11) |
-
voetnoot1)
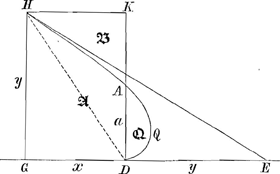
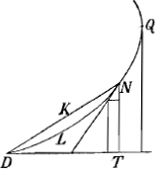
- Cet appendice, emprunté aux pages 36 et 37 du Livre J, contient la quadrature de la courbe DQAH de la deuxième figure de la Lettre No. 2813, pour laquelle on a toujours DE=HG=y et dont la soustangente s'exprime alternativement pour les différentes parties de la courbe, en valeur absolue, par les expressions x-y, y-x et x+y. Nous y avons apporté une division en paragraphes et nous nous sommes permis quelques changements dans les notations pour les rendre plus consistantes entre elles et avec celles de la figure citée de la Lettre No. 2813.
-
voetnoot2)
-
Quadrature de la partie inférieure, jusqu'au point Q, où la soustangente, pour DT=x, NT=y, s'exprime par x-y.
-
voetnoot3)
- Les sommations ne présentent aucune difficulté pour Huygens, puisqu'elles s'étendent depuis le point D, où x=0, y=0.
-
voetnoot4)
-
Quadrature complète de la partie DQhAD.
-
voetnoot5)
- Les sommations s'étendent ici depuis A jusqu'au point Q. Les dy représentent les décroissements de y. Voir encore pour la sommation des ydy la note 10.
-
voetnoot6)
- Pour le point Q, où la soustangente y-x s'annule, on a y=x=v, en conséquence
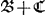 représente un carré dont l'aire égale vv. représente un carré dont l'aire égale vv.
-
voetnoot7)
- D'après le paragraphe précédent on a DLQD=¼ QN2=¼vv, donc
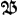 =DRQ++¼vv=¾vv. =DRQ++¼vv=¾vv.
-
voetnoot8)
-
Quadrature partielle de la partie intermédiaire (depuis A jusqu'à Q, voir la figure du § II), où la soustangente s'exprime par y-x.
-
voetnoot9)
-
Quadrature de la partie supérieure (depuis A), où la soustangente, pour DG=x, GH=y, s'exprime par y+x.
-
voetnoot10)
-
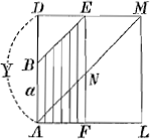
On rencontre sur la même page cette démonstration sous la forme suivante: ‘Si AB minima των y=a, AD maxima, seu Y. Erit 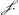 ydy=½YY-½aa, sit enim tunc ydy=½YY-½aa, sit enim tunc 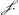 ydy=trapez. BEFA quod aequale ANED, quod aequale triang.o ADM-triang. NEM, hoc est ½YY-½aa. ydy=trapez. BEFA quod aequale ANED, quod aequale triang.o ADM-triang. NEM, hoc est ½YY-½aa.
-
voetnoot11)
- C'est-à-dire dans tous les cas divers, traités dans cet appendice.
|
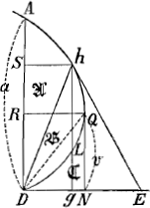
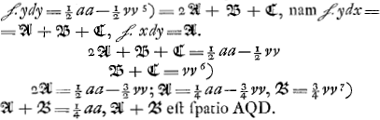
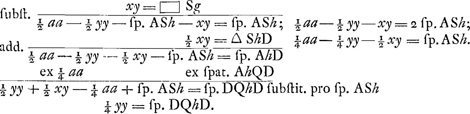




 ydy; sp. ASh=
ydy; sp. ASh=