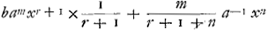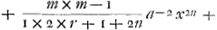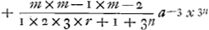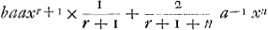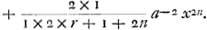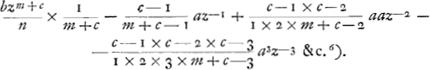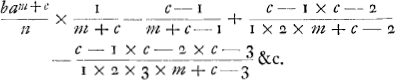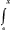Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–
[pagina 481]
| |||||||
No 2815.
| |||||||
[pagina 482]
| |||||||
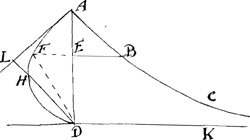 la constante a. Soit menée d'un de ses points quelconques B une parallele BF à DK qui rencontre AD au point E, sur laquelle soit prise la partie EF=DE×EB/a. je dis que le point F est à la courbe cherchée. Jl est à remarquer que si l'on mene les lignes AL, DL qui fassent sur AD des angles demi-droits; AL sera touchante en A, et DL coupera la courbe qui passe par tous les points F en deux portions HA, HD telles que la superieure HA a toutes ses soutangentes egales à y-x, et l'inferieure HD les a egales à x-yGa naar voetnoot2). Le segment DF est égal au quart du quarré de DEGa naar voetnoot3), de sorte que l'espace entiere AHDA est égal au quart du quarré de AD. La distance du centre de gravité du segment DF à la droite DK=4/9 DE, et à la droite DA==4/9EF+4/27 DEGa naar voetnoot4). Je puis aussi determiner les centres de gravité des solides faits par la revolution de ce segment tant autour de DK que de DA. 4o. Comme je n'ai point vu ce que Mrs. Neuton et Gregori ont trouvé pour les quadratures des lignes courbes, j'ai essayé si je ne pourois point venir à bout de celles qui sont comprises sous la formule que vous m'avez envoyé y=b xr×(xn+a)m, et j'ay trouvé deux suittes differentes qui donnent à ce que je pense tout ce qu'on peut souhaitter la dessus.
| |||||||
[pagina 483]
| |||||||
il est clair que le nombre des termes de cette suitte est infini lorsque m est un nombre rompu, et au contraire que le nombre en est fini c'est-à-dire que la suitte est interrompue lorsque m est un nombre entier. Or je dis que dans l'un et l'autre cas la somme de cette suitte exprime la quadrature de l'espace, qui a pour abcisse la ligne x que l'on suppose donnée. Soit par exemple m=2, la quadrature sera
Car tous les autres termes seront chacun egaux à zero puisqu'ils se trouvent tous multipliés par m-2=0. On suppose dans cette autre pour abbreger xn+a=z et r=cn-1
Il est clair que le nombre des termes est infini lorsque c est un nombre rompu, et qu'il est fini lorsque c est un nombre entier. Or je dis que dans l'un et l'autre cas la somme de cette suitte exprime la quadrature de l'espace: mais il faut observer d'en retrancher cette autre suitte.
Soit par exemple c=2, on aura pour la quadrature, | |||||||
[pagina 484]
| |||||||
On peut faire ici une remarque fort curieuse, savoir que la 1re suitteGa naar einda) nous en fournit une infinité, dont le nombre des termes est infini et dont on a la valeur par le moyen de la 2e suitte ce qui est reciproque. Mandez moi je vous prie si je suis tombé dans la regle de Mr. GregoriGa naar voetnoot7), ou si cela n'est pas laquelle des deux est la plus simple. On n'a point ici le livre de Wallis de Algebra et ainsi vous me feriez un plaisir singulier si vous vouliez bien m'envoyer par la poste les inventions de Mr. Neuton copiées de ce livre lorsque vous les aurez receuës et que vous en aurez fait faire une copie. 5e. La courbe de Mr. BernoulliGa naar voetnoot8) est geometrique lorsque la raison de BC à ACGa naar voetnoot9) est de nombre à nombre, et elle est transcendentale lorsque cette raison n'est pas de nombre à nombre. Ma construction suppose alors la quadrature de l'hyperbole, ce qui me paroist le plus simple dans ce genre. Je vous en ferai part quand vous le souhaiterez comme aussi de la maniere dont j'y suis parvenu ou vous verrez quelque chose d'assez curieux. Je n'avois point vû lorsque je vous ecrivis la dernière fois le journal de Leipsic ou Mr. Bernoulli avoit proposé son prob. Il l'avoit envoyé ici à un de ses amis pour en demander la solution à nos mathematiciens. J'ai receu depuis ce journal qui est du mois de May et j'ay esté surpris d'y trouver certaines choses touchant le probleme de Mr de BeauneGa naar voetnoot10) qui m'obligent à vous faire ici un petit destail. Lorsque Mr Bernouilli étoit à Paris il me vint voir et m'ayant dit qu'ils avoient fort travaillé son frere et lui sur l'inverse des tangentes, je lui proposé d'abord le probleme de Mr de Beaune, dont il est vrai qu'il m'apporta la solution quelque temps après qui n'étoit pas beaucoup differente de la mienne que je fis inserer depuis dans le 34.e journal des Sçavans sous le nom de Mr G***, qui est la 1re lettre de mon nom de baptesme m'appellant Guillaume et ayant des raisons alors pour cacher mon nom. Jl y a apparence que Mr. Bernoulli ayant vû dans vôtre lettreGa naar voetnoot11) que vous m'attribuyez cette invention et voulant avoir part à la gloire qui me paroist très petite, il s'est depesché de faire mettre dans les actes de Leipsic ce que vous y verrez. Mais ce qui m'a encore surpris davantage, ce sont ses parolles: curva autem AIGa naar voetnoot12) &c. Car s'il a bonne memoire il doit se ressouvenir que je lui communiquai alors les dimensions de ces deux courbesGa naar voetnoot13) en revanche de ce qu'il m'avoit communiqué | |||||||
[pagina 485]
| |||||||
touchant la funiculaire, la voiliereGa naar voetnoot14) &c. Cela me rendra à l'avenir plus circonspect à l'egard de certaines gens. Je n'ai pourtant pas laissé de lui écrire depuis pour me plaindre de son procedé qui me paroist fort irrégulier, et pour lui envoyer ma solution de son probleme afin qu'il la fasse inserer lui mesme dans les journaux de leipsicGa naar voetnoot15), et qu'ainsi il ne s'avise pas d'insinuer qu'il m'en auroit fait part autrefois. En voila plus qu'il n'en faut sur ce sujet et si je n'etois persuadé que vous me faites l'honneur d'estre de mes amis je ne vous aurois pas fait tout ce destail qui ne peut estre qu'ennuyeux étant sur que ceux qui me connoissent sauront bien demesler la verité. Je vous suis fort obligé Monsieur de la peine que vous avez prise de mettre par ordre la regle inverse des tangentes de Mr fatio. Je ne l'ai pas encore examinée avec soin: mais à la 1re inspection elle me paroist fort bornée et bien moins étenduë que celle dont je vous ai fait part car pour ce qui est de la soutangente de la conchoïde elle est si facile qu'il n'est besoin d'aucune methode pour la resoudre et d'ailleurs on suppose dans la mienne qu'on ait essayé auparavant si on ne peut point rendre tous les termes purs. Vous ne me parlez point de la regle que vous avez de Mr leibnitzGa naar voetnoot16) mandez moi je vous prie si elle est plus generale que la mienne, je serois bien aise aussi de voir de quel artifice vous vous servez pour rendre les soutangentes intraitables par nos methodes cela me serviroit peut-estre à la rendre plus generale. Je suis Monsieur avec toute l'estime imaginable vôtre treshumble et tres obeissant serviteur
Le M. de l'Hospital.
J'ai de quoi éclaircir vos difficultez sur la feuille de Mr. DescartesGa naar voetnoot17) mais ce sera à la 1re occasion. |
|


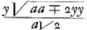 , et multipliant de part et d'autre par dy on trouve xdy=
, et multipliant de part et d'autre par dy on trouve xdy=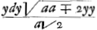 . De sorte que la somme des
. De sorte que la somme des