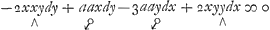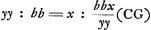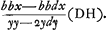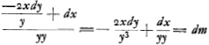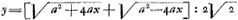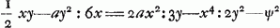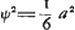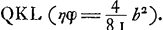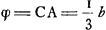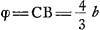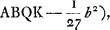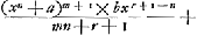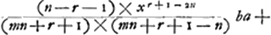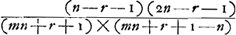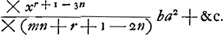Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–No 2810.
| |||||||
[pagina 458]
| |||||||
Il y a tout plein de belles choses dans ces 2 lettres, mais de la maniere que vous les expliquez, vous m'avez laissè bien des choses à dechifrer; comme de trouver la valeur de dm quand on a posè x ∞ myy, ou my, ou autre quantitè. Et puis de trouver ces mesmes positions artificieuses qui diminuent les termes de l'Equation differentielle. Je suis pourtant à la fin venu à bout, ou peu s'en faut, de l'unGa naar voetnoot3) et de l'autreGa naar voetnoot4), et j'ay achevèGa naar voetnoot5) l'exemple de la soutangente 2x+x3/yy en posant x ∞ my2, d'ou vient dx ∞ yydm+2mydy, comme dans l'exemple de la soutangente 2x-yy/2x, et, après les substitutions, ydy ∞ dm/m3, et la ligne courbe xxyy+y4- | |||||||
[pagina 459]
| |||||||
-bbxx ∞ 0. Je me suis encore proposè la soutangente xx-aa/xGa naar voetnoot6), qui fait l'Equation diffe.le
xxdy-aady ∞ xydx, ou j'ay supposè x ∞ myGa naar voetnoot7), ce qui donne dx ∞ ydm+mdy/a, et apres les substitutions, -a4dy/y3 ∞ mdm. Et la courbe aa ∓ ∓ yy ∞ xx. Dans vostre exemple où l'Equation differ.le est axydx++aaxdx+x3dx ∞ a3dy+axxdy, en supposant aa+xx ∞ am je trouve bien comme vous Monsieur mdy ∞ ½ydm+½mdm; mais en supposant en suite selon la regle, y ∞ nm½, je ne scay pas comment vous en tirez dn ∞ ½m-½ dm ou ½ dm/√m. C'est pourquoy permettez que je vous demande icy quelque eclaircissement. Dans ce que vous avez touchant la quadrature de la courbe xx ∞ aayy∓2y4/2aa, je n'entens pas comment vous trouvez xdy ∞ 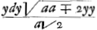 . Il semble que de l'Equation
x- . Il semble que de l'Equation
x-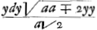 ∞ 0 vous trouviez la soutangente ∞ 0 vous trouviez la soutangente 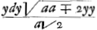 ce qui ne suit pas par la regle ordinaire des soutangentes. Je ne vois pas non plus par ou vous trouvez la somme des ce qui ne suit pas par la regle ordinaire des soutangentes. Je ne vois pas non plus par ou vous trouvez la somme des 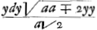 ; et cela n'est pas moins difficile peut-estre que de trouver simplement et sans calcul differentiel la quadra- ; et cela n'est pas moins difficile peut-estre que de trouver simplement et sans calcul differentiel la quadra- | |||||||
[pagina 460]
| |||||||
ture de cette courbe; à quoy j'ay 2 methodesGa naar voetnoot8), qui, quand la courbe est xx ∞ aayy-2y4/aaGa naar voetnoot9) me donnent le complement 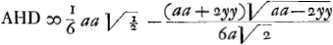 Ga naar voetnoot10). Ga naar voetnoot10).
 J'ay tres bien compris vos exemples de la Courbe de Mr. de BeauneGa naar voetnoot11) et de celle à la soutangente x+y, qui sont deux problemes tres beaux et heureusement resolus. J'ax essaiè de chercher la courbe de la soutangente x-yGa naar voetnoot12), mais sans y reussir, et je seray bien aise de voir si et comment elle se trouve par vostre methode. Pour la courbe de Mr. Bernouilly le medecin, j'admire extremement comment vous l'avez pu attraper puis que la soutangente en est si compliquee. Je ne veux pas encore vous demander le secret de cette invention, mais seulement quelle sorte de courbe c'est et si elle se peut construire par la quadrature de l'hyperbole. En fin Monsieur vostre methode est un chemin nouveau pour les belles decouvertes en Geometrie, et où je conçois un progres et une speculation infinie à cause de la varietè des PositionsGa naar voetnoot13), touchant les quelles il reste à scavoir si on en peut trouver d'utiles dans toute rencontre. Mr. Bernoulli peut-estre a quelque chose de semblable, puis qu'apparemment il sait resoudre le Probleme qu'il a propose. Je n'ay pas encore vu ces Acta de Leipsic, où vous l'avez trouvè, par la faute de nos libraires. | |||||||
[pagina 461]
| |||||||
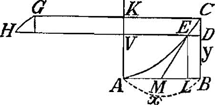
Vous dites que vous m'envoiez les 3 differentes voiesGa naar voetnoot14) pour la quadrature de la Feuille, et il semble cependant que vous ne m'en envoiez pas une. Car dans la premiere vous n'expliquez point comment on connoit que la somme des ayydx-2axydy/6xx est -ayy/6x, ce que je doute fort si je pourray trouver par vostre methode de cy-dessus. Dans la 2e maniere, où vous supposez y ∞ zxx/aa, j'ay fait tout le calculGa naar voetnoot15) qui confirme le vostre et toutefois 2axx/3y-x4/2yy n'est pas la valeur du triligne ABC,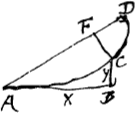 mais l'excede de ⅙ aa, c'est-à-dire de toute la Feuille. De quoy il faloit bien avertir, et faire voir (ce qui me paroit assez difficile) que cela arrive necessairement, parce qu'autrement on s'abuseroit en suivant cette maniere. Je me suis servi en cherchant la quadrature de cette courbe de la mesme supposition y ∞ zxx/aaGa naar voetnoot16), mais je poursuis autrement, sans calcul differentiel, ou je trouve la veritable grandeur de l'espace ABC ∞ ½ xy-ayy/6x.
La 3e maniere, où vous vous servez de la relation entre AF et l'appliquée CF, vous avez voulu la reserver pour une autre fois. Ayez la bontè je vous prie de vous en souvenir, et de rendre les choses un peu plus claires. J'ay considerè cy devant la relation de ces lignes AF, FC pour chercher le solide par la conversion de la demie feuille ACD sur son axe AD, et ses parties, que je trouve dependre | |||||||
[pagina 462]
| |||||||
de la quadrature de l'hyperbole, et dans le solide entier seulement du logarithme de 2Ga naar voetnoot17). Mr. Gregory Professeur à OxfordGa naar voetnoot18) est venu faire un tour en ce pais, et a bien voulu me communiquer sa Regle pour les quadratures, qui est pour certain ordre de lignes courbes dont les equations sont comprises de cette formule y ∞ bxr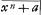 m, ou a et b sont des quantitez connues, y est l'appliquée, x l'abcisse, r, n, m des exponants indeterminez et qui peuvent estre affirmatiss ou negatifs, comme aussi les signes devant les quantitez bxr, xn et aGa naar voetnoot19). Il a fait une m, ou a et b sont des quantitez connues, y est l'appliquée, x l'abcisse, r, n, m des exponants indeterminez et qui peuvent estre affirmatiss ou negatifs, comme aussi les signes devant les quantitez bxr, xn et aGa naar voetnoot19). Il a fait une
| |||||||
[pagina 463]
| |||||||
recherche merveilleuse par les series pour venir à cette RegleGa naar voetnoot20). Il dit que Mr. Newton l'a aussi trouvée par un autre chemin et encore quelque chose de plus; | |||||||
[pagina 464]
| |||||||
ce que vous verrez, ou l'avez desia vu, dans ce qu'on a publiè de lui dans le livre de WallisGa naar voetnoot21); c'est pourquoi il n'est pas besoin que je vous explique icy la regle de Mr. Gregory. On m'a promis ces inventions de Newton copiées du dit livre, mais je n'ay encore rien receu. Apres ce que vous m'avez appris touchant les horloges de Mr. Hautefeuille, je ne doute point qu'elles ne reussissent mal, puis que les mienes avoi[en]t du commencement de ces balanciers pesantsGa naar voetnoot22) qui estoient sujets à s'arrester et usoient les trous des pivots. Le meilleur est de faire leur cercles grands et legers, parce que la grandeur fait qu'ils reglent mieux le mouvement de la montre que s'ils estoient moins etendus avec le mesme poids. Pour le charme de la baguette, j'en suis fort en repos depuis les relations que j'en ay vues dans nos journaux et la decision de Mr. le Prince. Voicy la Regle inverse des Tangentes de Mr. FatioGa naar voetnoot23), que vous n'aurez pas de peine a comprendre, mais j'en auray un peu a la rediger en forme, parce que ni l'autheur ni moy ne nous en sommes jamais donnè la peine. Vous scavez Monsieur comment d'une equation de courbe donnée, on forme l'equation differ.le scavoir en multipliant chaque terme par l'exposant de x et en changeant un x en dx, et en multipliant chaque terme par l'exposant de y et changeant un y en dy, et negligeant les termes qui n'ont que des quantitez connues. Ainsi de l'équation de courbe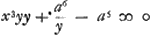 , il vient la differ.le , il vient la differ.le 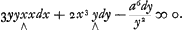 Vous scavez aussi comment l'equation differentielle de la courbe se trouve lors que la soutangente est donnée. Et vous ne pouvez ignorer comment d'une Equation differ.le simple, on revient à l'Equation simple de la courbe, dont elle est produite. J'appelle Equation simple de la courbe, celle qui n'a point de fractions ou il y ait y, ou x, ou tous les deux, dans le denominateur. Car, par exemple vous voiez dans l'Equation differ.le
Vous scavez aussi comment l'equation differentielle de la courbe se trouve lors que la soutangente est donnée. Et vous ne pouvez ignorer comment d'une Equation differ.le simple, on revient à l'Equation simple de la courbe, dont elle est produite. J'appelle Equation simple de la courbe, celle qui n'a point de fractions ou il y ait y, ou x, ou tous les deux, dans le denominateur. Car, par exemple vous voiez dans l'Equation differ.le 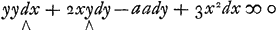 , qu'il y a deux termes correspondants marquez ∧, c'est a dire qui, exceptè les nombres prefigez, , qu'il y a deux termes correspondants marquez ∧, c'est a dire qui, exceptè les nombres prefigez,
| |||||||
[pagina 465]
| |||||||
ont toutes les mesmes lettres, en comptant dx pour x et dy pour y. Et que de l'un ou de l'autre de ces termes on peut d'abord trouver leur generateur commun xyyGa naar voetnoot24) en changeant dans l'un dx en x, et divisant apres par l'exposant de x qui est icy 1, ou en changeant dans l'autre dy en y et divisant alors par l'exposant de y. Et que de chacun des deux autres termes non correspondants, et qui n'ont que x ou y, on en tire leurs termes generateurs -aay+x3, de sorte que l'Equation de la courbe est xyy-aay+x3 ∞ 0. On connaitra donc que la soutangente et l'Equation differ.le qui en est formée, sont simples, lors qu'on verra, ou que tous les termes de cette Equation sont purs, c'est a dire qu'ils ne contienent point x et y ensemble, ou que chaque paire de termes correspondans peut venir d'un mesme terme generateur. Or la Regle de Fatio ne fait autre chose que de trouver l'Equation de la courbe lors que la soutangente ou l'Equation differentielle est formée d'une Equation de courbe qui n'est pas simple, mais deguisée, c'est-à-dire qui a une ou plusieurs fractions ou il y a x ou y, ou tous les deux, dans le denominateur, au quel cas il n'est pas si aisè de demesler quels sont les termes generateurs qui composent l'Equation de la courbe. Et il faut scavoir que tres souvent les soutangentes ou deguisées expres ou simplement données, et aussi l'équation differentielle, qui en est formée, sont telles, comme si l'une et l'autre avoient este formées d'une Equation deguisée de ligne courbe. Par ex. de l'Equation simple xyy-aay+x3 ∞ 0, on a, par la regle connuë des tangentes, la soutangente simple -2xyy+aay/yy+3xx ou, mettant pour 3xx sa valeur 3aay-3xyy/x, on aura la soutangente deguisée -2xxy+aax/3aa-2xy, une de celles que je vous avois proposéesGa naar voetnoot25). Et l'Equation differ.le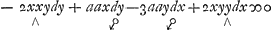 , la quelle provient aussi de l'equation y2/x2-aay/x3+1 ∞ 0, qui est la premiere deguisée par la multiplication par 1/x3. , la quelle provient aussi de l'equation y2/x2-aay/x3+1 ∞ 0, qui est la premiere deguisée par la multiplication par 1/x3.
Voicy donc comme j'explique la Regle de Mr. Fatio. Estant donnè quelque soutangente, on en formera l'Equation differ.le. Et apres qu'on aura reconnu, comme il a estè montrè, qu'elle est deguisée, on verra s'il y a une ou plusieurs paires de termes correspondants, tels que je les ay desinis, quoy qu'ils ne puissent pas provenir d'un mesme terme generateur. Ainsi dans l'equation differentielle, qu'on vient de voir, il y a deux paires de termes correspondans marquez ∧ et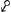 . Que s'il y a, outre les termes correspondants, . Que s'il y a, outre les termes correspondants,
| |||||||
[pagina 466]
| |||||||
il y a [sic] des termes, qui n'aient point de corresp.s ou que tous soient tels, et que dans ce nombre il y en ait meslez de x et y, il faut voir si, en multipliant l'Equation par quelque puissance de x ou de y, ou de tous les deux, on peut rendre tous ces termes purs. Si non, l'Equation est intraitable et la Regle ne peut point servir. Ainsi dans l'Equation differ.le 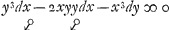 , outre les termes marquez , outre les termes marquez 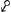 , qui sont correspondants, il y a le terme meslè x3dy, qui deviendra pur en multipliant l'equation par 1/x3. Et apres cette multiplication, qui sera y3dx/x3-2yydy/xx-dy∞0, les termes correspondants demeureront necessairement tels. , qui sont correspondants, il y a le terme meslè x3dy, qui deviendra pur en multipliant l'equation par 1/x3. Et apres cette multiplication, qui sera y3dx/x3-2yydy/xx-dy∞0, les termes correspondants demeureront necessairement tels.
Mais si l'Equation deguisée consiste toute en termes correspondants, ou qu'outre ceux-cy elle en contiene de purs sans la dite multiplication, ou qu'après cette multiplication les termes corresp.s ne puissent pas encore venir deux à deux d'un mesme terme generateur, alors il faut chercher ce qu'on appellera le Transformateur de cette Equation, composè de quelques puissances de x et y ensemble, ou de l'un des deux, qui multipliant l'Equation, rende tels les termes correspondants, que 2 à 2 ils puissent venir d'un mesme terme generateur, et en sorte que les autres purs ne deviennent meslez de x et y. Soit par ex. pour l'Eq.on differ.le de cy-dessus
le Transformateur xg yh, ou g et h sont ces puissances de x et y que l'on cherche. Je scay que dans le terme generateur, d'ou je veux que les termes marquez ∧ puissent estre produits les exposants de x et de y doivent estre entr'eux comme les nombres prefigez+2 à-2, comme il s'ensuit de la maniere susdite de former les equations differentielles. Mais l'exposant de x, apres la transformation, sera g+2, parce que dans ces termes il y a desia xdx ou x2. Et l'exposant de y sera h+2 parce qu'il y a desia dans ces termes ydy ou y2. Donc g+2 sera à h+2, comme+2 à-2, d'ou h est ∞-g-4Ga naar voetnoot26). Je scay de mesme que dans le terme generateur, d'ou les termes correspondants aaxdy et-3aaydx doivent naitre, les exposants de x et de y doivent estre comme les nombres prefigez -3 à+1. Mais l'exposant de x après la transform.on sera g+1, parce qu'il y a desia x ou dx, et l'exposant de y sera h+1, parce qu'il y a desia dy ou y. Donc g+1 à h+1 comme -3 à+1; d'où vient | |||||||
[pagina 467]
| |||||||
3h ∞-g-4Ga naar voetnoot27). Mais on avoit h ∞-g-4, donc h ∞ 3h et h ∞ 0. et g ∞-4, c'est a dire que le transformateur xg yh sera 1/x4. Multipliant maintenant l'equation par ce 1/x4 on aura: 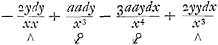 ∞ 0.
Ou l'on voit que les deux termes corresp.s marquez ∧ ont un mesme generateur-yy/xx et que les deux marquez ∞ 0.
Ou l'on voit que les deux termes corresp.s marquez ∧ ont un mesme generateur-yy/xx et que les deux marquez 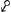 ont un mesme generateur aay/x3, de sorte que l'equation deguisée de la courbe est-yy/xx+aay/x3 0/+∞ 0 et la simple: -xy+aa ∞ 0, ou-xyy+aay ∓ x3 ∞ 0.
Dans l'Equation differentielle de cy dessus y3dx-2xyydy-x3dy ∞ 0, qui estant multipliée par 1/x3, estoit devenue ont un mesme generateur aay/x3, de sorte que l'equation deguisée de la courbe est-yy/xx+aay/x3 0/+∞ 0 et la simple: -xy+aa ∞ 0, ou-xyy+aay ∓ x3 ∞ 0.
Dans l'Equation differentielle de cy dessus y3dx-2xyydy-x3dy ∞ 0, qui estant multipliée par 1/x3, estoit devenue 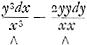 -dy ∞ 0, les deux termes correspondants ne peuvent pas encore venir d'un mesme generateur, de sorte qu'il faut chercher un Transformateur xg yh. Or on trouve g-2 à h+3 comme 1 à -2, et partant-2 g+1 ∞ h, mais g doit estre ∞ 0, parce qu'autrement en transformant l'Equation, le terme pur - dy deviendroit meslè. Donc h est ∞ 1 et le Transsormateur est y, l'Equation transformée -dy ∞ 0, les deux termes correspondants ne peuvent pas encore venir d'un mesme generateur, de sorte qu'il faut chercher un Transformateur xg yh. Or on trouve g-2 à h+3 comme 1 à -2, et partant-2 g+1 ∞ h, mais g doit estre ∞ 0, parce qu'autrement en transformant l'Equation, le terme pur - dy deviendroit meslè. Donc h est ∞ 1 et le Transsormateur est y, l'Equation transformée 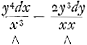 -ydy ∞ 0. Et icy le terme generateur des deux correspondants est -y4/2xx; et le generateur du terme pur sera -yy/2. L'Equation deguisée de la courbe est donc -y4/2xx-yy/2+aa ∞ 0, et l'Equation simple -y4-xxyy+2aax2Ga naar voetnoot28).
Dans l'Equation -ydy ∞ 0. Et icy le terme generateur des deux correspondants est -y4/2xx; et le generateur du terme pur sera -yy/2. L'Equation deguisée de la courbe est donc -y4/2xx-yy/2+aa ∞ 0, et l'Equation simple -y4-xxyy+2aax2Ga naar voetnoot28).
Dans l'Equation 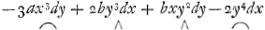 ∞ 0, les termes marquez ∧ sont correspondants; les autres marquez ◠ sont point correspondants, ni purs, mais meslez. Mais on voit d'abord qu'ils peuvent devenir purs en multipliant l'Equ.on par 1/x3y4, et point autrement; après quoy on aura ∞ 0, les termes marquez ∧ sont correspondants; les autres marquez ◠ sont point correspondants, ni purs, mais meslez. Mais on voit d'abord qu'ils peuvent devenir purs en multipliant l'Equ.on par 1/x3y4, et point autrement; après quoy on aura
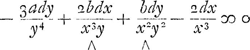 | |||||||
[pagina 468]
| |||||||
et en mesme temps on voit que les termes correspondants ont un commun generateur -b/xxy; que si cela n'eust point estè ainsi, l'Equation estoit intraitable. Maintenant l'Equation deguisée de la courbe sera a/y3-b/x2y+1/x2 ∞ 0, et la simple axx-byy+y3 ∞ 0. Dans l'Equation x4dx+bx3dx+bccdxGa naar voetnoot29)+bbccdx+x3ydy ∞ 0, qui vient de la soutangente de la Conchoide, et qui ne reçoit point de forme convenable pour la preparer à vostre methode, il n'y a aucuns termes correspondants; mais on voit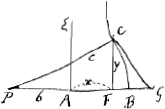 qu'en divisant par x3, tous les termes devienent purs, puis qu'on a xdx+bdx+bccdx/xx+bbccdx/x3+ydy ∞ 0, de sorte qu'il ne faut que tirer de chacun de ces termes son generateur, et en adjoutant à tous ces generateurs la quantité connue ½bb-½cc, on aura l'equation de la ConchoideGa naar voetnoot30). Et ce sera une autre courbe, dont la soutangente s'exprime de mesme, si on n'y adjoute ni n'oste aucune quantité connue. Dans tous les exemples precedents et dans plusieurs autres que j'ay examinez, j'ay vu que les Equations differentielles admettoient la forme convenable pour vostre methode; mais par ce dernier il semble que celle de Mr. Fatio peut servir ou la vostre n'a point lieu, comme par vostre exempleGa naar voetnoot31) où vous posez xx+aa ∞ am, il paroit que vostre methode peut servir mesme dans des courbes geometriques ou la siene demeure court, outre le grand usage de la vostre dans les Courbes Transcendantes. Cependant il manque encore à toutes les deux methodes, qu'elles ne servent pas pour les soutangentes deguisées de certaine maniere, comme sont les deux que je vous avois proposéesGa naar voetnoot32); mais il n'y a rien que je n'attende de vous Monsieur, après tout ce que j'ay vu. Je vous prie très humblement de me faire response sur les doutes que j'ay marqués et de me croire avec beaucoup de respect &c.
a la Haye ce 23 Jul. 1693. |
|