Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–
[pagina 469]
| |||
No 2811.
|
| 2m dm=dy/y3 sive dy. y-3Ga naar voetnoot2). |
| Summae sunt mm=½y-2 sive 1/2yy. |
Regula universalis est ut pro dm vel dy vel qualibet alia differentia, ponatur ipsa m vel ipsa y, ac porro divisio fiat per exponentem incognitae qualisque tunc erit.
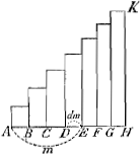
Singulae AB, AC, AD etc. sunt m, et AH maxima ipsarum. Singulae particulae aequales AB, BC, CD etc. sunt dm. Jam apparet summam omnium mdm esse triangulum AHK=½ qu. ex AH, hoc est ½ mm, ut nempe m hic intelligatur esse maxima omnium m.
Itaque summa omnium 2mdm erat=mm.
Sed dy/y3 idem quod b4dy/y3, adscito b4, ut fiat homogeneum του 2mdm.
Et summa omnium dy/y3=-½ y-2 sive-1/2yy idem quod-b4/2yyGa naar voetnoot3).
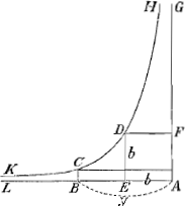
Si enim HDC sit hyperboloides cujus asymptoti GA, AB. AEDF quadr.m cujus latus AE=b. AB=y. BC=θ=b4/y3 ex natura hyperboloidis hujus. Erit ▭ CA=
=θy=b4/yy. Cujus dimidium b4/2yy erit aequale spatio infinite extenso BCKLGa naar voetnoot4). Hic nempe AB est minima omnium y, quae crescunt aequalibus particulis dy.
Si BC sive θ fuisset ex natura curvae=b3/y2, fuisset ▭ AC hoc est b3/y2 in y, hoc est b3/y=spatio infinite extenso BCKL nempe=summae omnium dy/yy sive dy y-2, ubi addita unitate ad exponentem fit-1, tumque divisio facienda per-1. Itaque-1/y hoc est-b3/y erit summa.
Si BC sive θ=bb/y fuisset ▭ AC=bb, idque divisum per 0 qui hic est exponens y, fit bb/0=spat. hyperb. infinitum BCKL, quod est magnitudine infinitumGa naar voetnoot5).
- voetnoot1)
- Cet appendice est emprunté à la page 21 du Livre J des Adversaria.
- voetnoot2)
- Comparez la Lettre No. 2805, de de l'Hospital à Huygens, où l'on rencontre dans la 1e question l'équation 2mdm=-dy:y3.
- voetnoot3)
- Dans ces expressions les signes - ont été intercalés plus tard.
- voetnoot4)
- La quadrature de ces aires hyperboloïdes était alors bien connue.
- voetnoot5)
- A la même page la règle est appliquée encore sans démonstration aux équations 4n3dn=aadm et dn=½m-½dm que l'on rencontre plus loin dans la même lettre de de l'Hospital à Huygens.

