Oeuvres complètes. Tome VII. Correspondance 1670-1675
(1897)–Christiaan Huygens–No 1891.
|
| Sit jam AM∞a | Quia ergo aequales anguli KHE et CHZ sive EHG |
| MB∞b | estque EHA angulus rectus, erit ut |
| AL∞c | KE ad EG ita KA ad AG, quia vero |
| LC∞n | BM ad MK ut HF ad FK erit ut |
| rad. AD∞d | BM + HF ad HF ita MF ad FK |
| AF∞x | b + y - - - - - y - - - a - x - - ay - xy / b + y |
| FH∞y | |
| add. FA xGa naar voetnoot3) fit KA ay + bx / b + y. |
Rursus, quia CL ad LG vt HF ad FG, erit permutenda et dividendo
CL-HF ad HF vt LF ad FG

quâ ablatâ ab AF ∞ x fit GA ∞
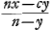 . Est autem EA ∞ dd/x, quia proportionales FA, AH, AE. ergo EA-GA, hoc est EG,
. Est autem EA ∞ dd/x, quia proportionales FA, AH, AE. ergo EA-GA, hoc est EG, 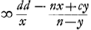 Ga naar voetnoot4). Et KA-EA hoc est, KE ∞
Ga naar voetnoot4). Et KA-EA hoc est, KE ∞ 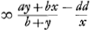 .
Sed diximus quod
.
Sed diximus quod
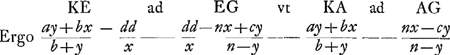
Unde invenitur
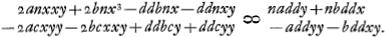
Et quia n ∞ bc/a fit
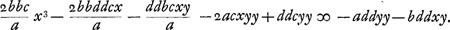
Est autem
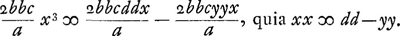
Ergo
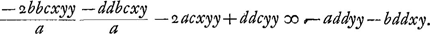

quae aequatio est ad hyperbolam.
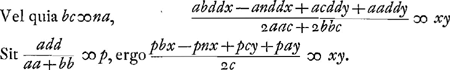
Vnde porro non difficulter invenitur sequens constructio.
Jungatur BA, ACGa naar voetnoot5) et applicato seorsim ad utramque quadrato radii AD, fiant inde AP, AQ, et junctâ PQ, dividatur ipsa bifariam in R, et per punctum R ducantur RDGa naar voetnoot6), RN sese ad rectos angulos secantes quarumque RDGa naar voetnoot6) sit parallela AD quae dividit bifariam angulum BAC. Erunt jam RDGa naar voetnoot6), RN asymptoti oppositarum hyperbolarum quarum altera per centrum A transire debet, quaeque secabunt circumferentiam in punctis H quaesitis. Transibunt autem hyperbolae per puncta P, Q.
Ratio constructionis apparet ductis Pγ et Qζ perpendicularibus in AM. fit enim Aγ ∞ add / aa + bb siue p. et Aζ ∞ ap/c. Item Pγ ∞ pp/c, et Qζ ∞ pb/c.
Quare AO ∞ pc + pa / 2c, et OR ∞ pb-pn / 2c. Unde caetera facilia.
- voetnoot1)
- Le No. 98, du 17 novembre 1673 [V. st.]. Voir aussi l'édition des Opera Varia de Huygens par 's Gravesande, Vol. II, p. 761.
- voetnoot2)
- Voir la figure No. 1 de la planche vis-à-vis de cette page.
- voetnoot3)
- C'est-à-dire FA = x.
- voetnoot4)
- On écrirait actuellement
 , ou
, ou 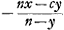
- voetnoot5)
- Voir la figure No. 2 de la planshe.
- voetnoot6)
- Lisez: Rh.
- voetnoot6)
- Lisez: Rh.
- voetnoot6)
- Lisez: Rh.

