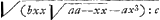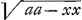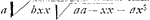Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 525]

N^o 2826.
Christiaan Huygens à J. le Clerc, rédacteur de la Bibliothèque Universelle et Historique.
[septembre 1693].

La minute se trouve à Leiden, coll. Huygens.
La pièce a été publiée dans la Bibliothèque Universelle et Historique¹⁾ et, en latin,
par W.J. 's Gravesande²⁾.

Remarque de M. Huguens sur le livre de la Manoeuvre des Vaisseaux imprimé à Paris en 1689, in-8^o. Pagg. 117³⁾.

Le Livre, dont l'Auteur est Mr. Renaud, Ingenieur Général de la Marine, est écrit avec beaucoup de soin, de netteté & de methode, & marque du sçavoir dans la Geometrie & dans l'Analyse. On n'y suppose point de principes que je n'avoüe être véritables⁴⁾; & si toute la Théorie étoit tirée de là par des conséquences legitimes, il n'y auroit rien à reprendre. Mais cela n'étant pas, je crois que pour l'utilité du public, il est bon d'avertir d'une erreur considerable que j'y ay reconnüe, parce que se répandant dans la plus grande partie des Régles qu'on donne ici aux Pilotes, elles pourroient les mener dans des erreurs tres grandes & dangereuses.

Je commencerai en raportant le contenu de l'Article I du 2. Chapitre où l'Auteur suppose le vaisseau HBM; dans lequel la ligne droite DC represente la position de la Voile, que l'on conçoit comme une surface plane, élevée perpendi-

1) Dans la livraison de septembre 1693, page 195. Voir, sur ce journal, la Lettre N^o. 2435, note 19.

2) Chr. Hugenii etc. Opera Varia, Volumen Primum, p. 292 sqq.

3) Voir, pour le titre complet, la note 17 de la Lettre N^o. 2813.

4) Il s'agit des principes exposés dans le premier Chapître, intitulé: ‘De la force du vent contre les voiles, de la force de l'eau contre le gouvernail, & de sa résistance contre le vaisseau’. Dans ce chapître Renaud expose, avec beaucoup de clarté, la théorie alors généralement reçue d'après laquelle la pression d'un fluide en mouvement contre une surface résistante, serait causée par les impulsions de ses particules matérielles se mouvant toutes, indépendantes les unes des autres, avec la même vitesse dans la même direction et frappant contre la surface. Par des raisonnements apparents cette théorie conduit à la conclusion, que l'on considérait comme rigoureusement vraie, que la pression mentionnée, toujours dirigée suivant une ligne perpendiculaire à la surface, devrait être en raison composée de l'aire de la surface, du carré de la vitesse relative du fluide et du carré du sinus de l'angle d'incidence.
Consultez encore, quant aux vues de Huygens sur la pression d'un fluide mouvant, la page 19 de la Lettre N^o. 2660.

[p. 526]

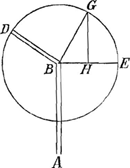
culairement sur cette ligne. AB est la ligne du vent qui pousse la voile. BG est perpendiculaire sur DC; GK perpendiculaire sur BK, qui est la quille du vaisseau



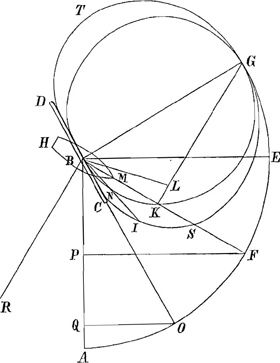prolongée. GEA est un arc de cercle decrit du centre B. BKG une circonference ayant BG pour diametre.

Il est vrai ce que dit l'Auteur, que la superficie CD est poussée par le vent AB suivant la ligne BG, de sorte que si le vaisseau fendoit l'eau de tous côtez avec la même facilité qu'il la fend avec sa pointe, il iroit au point G suivant la ligne BG. Il ajoûte que parcourant cette ligne il avanceroit de pointe de la quantité BK, & de côté de la quantité KG; mais que comme le vaisseau trouve beaucoup plus de difficulté a fendre l'eau avec le côté qu'avec la pointe, il n'avancera pas dans la determination KG de la quantité KG, mais qu'il s'en faudra une quantité proportionnée à la difficulté qu'il a de plus à fendre l'eau avec le côté qu'avec la pointe. Par exemple si la difficulté par le côté à celle par la pointe étoit comme dix à un, si l'on proportionne KG à KL comme 10. à 1, & qu'on tire la ligne BL, il dit que le vaisseau ira au point L, suivant la ligne BL, dans le même tems qu'il auroit été au point G, s'il fendoit l'eau de tous côtez avec la même facilité.

Il suffit d'avoir suivi l'Auteur jusqu'ici. Je dis que sa méprise consiste dans ce qu'il veut que le vaisseau soit parvenu de B en K⁵⁾ dans le même tems qu'il seroit parvenu de B en G. Car si nous supposons que la derive est nulle, pour avoir moins d'embarras, il est certain que, selon l'Auteur, le vaisseau ira encore de B en K dans le même temps qu'il iroit de B en G, prenant toujours qu'il fend l'eau de tous côtez avec la même facilité; ou bien en le faisant avancer de pointe, aussi bien en allant par BG qu'en allant par BK.

Il semble qu'en cela il ait raisonné de cette façon, sçavoir que si en allant de B en G, le vaisseau avance de côté de la quantité KG, & de pointe de la quantité BK, il saut que le mouvement dans le sens KG lui etant ôté, il lui reste le mouve-

5) Lisez: L.

[p. 527]

ment dans le sens BK par lequel la ligne BK étoit parcourrüe en même tems que BG.

Mais il falloit considerer que bien qu'on puisse imaginer que le mouvement du vaisseau par BG est composé des mouvemens par BK & par KG, il ne s'ensuit pas que si dans l'effet on lui laisse le seul mouvement suivant BK; (soit que la figure & la position du vaisseau en soit cause, soit qu'on le suppose attaché par une corde infiniment longue BR, qui soit perpendiculaire à BM) il ne s'ensuit pas, disje, que le vent qui, en pressant la voile CD, le pousseroit de B en G, le poussera dans un tems égal de B en K. Car pour sçavoir quel espace il parcourra par BK, il faut voir avec quelle force il est poussé dans cette route, & de plus avoir égard à la resistence qu'il souffre de l'eau. Or il est certain, par les regles de Mechanique, que la force avec laquelle la voile DC pousse le vaisseau par BK, est à celle dont la même voile, & dans la même position à l'égard du vent, le pousseroit par BG, comme BK à BG; & l'Auteur en convient dans ce qu'il explique des impressions de l'eau contre le Gouvernail, au 5. Article de ce second Chapitre⁶⁾. Mais les vitesses seroient aussi comme BK à BG, puis que l'on veut que ces deux lignes soient parcourües dans des tems égaux. Donc les forces seroient comme les vitesses; ce qui ne sçauroit être, & repugne à ce que l'Auteur à demontré au 13. Art. du I Chap. où il dit, que pour faire mouvoir un corps avec différens degrez de vitesse dans une matiere fluide, il faut que les puissances que le font mouvoir soient en raison des quarrez des vitesses. Donc les lignes BK, BG ne sont pas parcourües en des tems égaux. Mais pour sçavoir quel espace le vaisseau doit parcourir dans la route BK, il faut prolonger BK en S, en sorte que BS soit moienne proportionelle entre BK, BG. Alors BS sera l'espace qu'il parcourra dans le même tems qu'il iroit par BG, s'il fendoit l'eau dans ce sens avec la même facilité. Car icy les quarrez des vitesses par BG & BS, & par conséquent aussi les resistences de l'eau, seront comme BG à BK; mais, comme je viens de dire, la proportion des forces est encore comme BG à BK; donc les forces seront comme les resistences & aussi comme les quarrez des vitesses. Et par consequent ce sont ces vitesses, qui sont comme BG à BS, que le vaisseau doit acquerir dans ces deux routes, selon la maxime de l'Auteur que je viens de citer, & qui ne reçoit point de doute.

Ce n'est donc pas, comme il a cru, la circonference du cercle BKG qui determine les espaces que le vaisseau doit parcourir dans les diverses positions de sa quille, avec la même disposition de la voile CD à l'égard de la ligne du vent; mais c'est la courbe BISGT, dont on trouve facilement les points de même qu'on a trouvé S. Et il est à noter que les espaces qu'elle donne, different d'autant plus de

6) On y lit en effet: ‘si BG’ [il s'agit de l'hypothénuse d'un triangle rectangle BFG] ‘représente la force avec laquelle le gouvernail est poussé, BF sera la force avec laquelle il est poussé dans la détermination BF & FG celle dont il est poussé dans la détermination FG’.

[p. 528]

ceux que l'Auteur termine par la circonference BKG, que l'angle de la quille avec la ligne du vent devient plus aigu. Ainsi dans la route par BN, le vaisseau ira par BI, qui sera double de BN enfermée dans le cercle, si BN est ¼ de BG; & il sera le triple de BN, si BN est 1/9 de BG.

La même erreur que je viens de remarquer inflüe dans presque tout le reste du Traité, & empêche de subsister plusieurs Theorêmes qui autrement paroissent fort élegants. Comme entre autres celui qui dit⁷⁾ que quand l'Angle de la voile avec le vent, OBA, est donné; la plus avantageuse situation de la quille, pour gagner au vent, est celle qui divise également son complement OBE, d'où l'Auteur trouve en suite, en supposant que la derive est nulle, que la plus avantageuse situation de la quille & de la voile ensemble pour cela, seroit lorsque l'angle du vent & de la quille est de 60. degrez, & celuy du vent & de la voile de 30. Ce qui n'est point, car par une Regle que je sçai être vraie, quand l'angle du vent & de la quille est de 60. degrez, si on fait l'angle de la voile & du vent de 39. degrez 23. le vaisseau avancera plus dans sa route, & par consequent gagnera plus au vent, que quand la voile avec le vent fait un angle de 30 degr.⁸⁾. Cette Regle par laquelle je trouve la plus avantageuse situation de la voile quand l'angle de la quille & du vent⁹⁾ est donné, pour faire le plus de chemin, est telle x⁴=aaxx+1/3 ppxx-4/9aapp.

7) On le rencontre à la page 39 du Chapître IV, intitulé: ‘De la maniere de determiner la situation la plus avantageuse de la voile & de la Prouë, pour tenir le vent le plus qu'il est possible’.

8) On rencontre aux pages 70 et 71 du livre J, à propos de ce theorème, qu'on trouve à la page 50 du Chapître cité dans la note précédente, la remarque suivante, dont nous avons accommodé la notation à celle de la figure du texte: ‘Supposant qu'il n'y a point de derive, il trouve la situation de la voile la plus avantageuse quand elle fait avec le vent l'angle ABO de 30 degr.; donc divisant le complement OBE par le milieu en F, la situation de la quille seroit BF, qui seroit donc la plus avantageuse ensemble avec celle de la voile, pour gagner au vent, mais par ma Regle, lors que la quille est selon BF, je trouve une situation plus avantageuse pour la voile que celle qui coupe l'angle ABF egalement pour gagner au vent. Parce qu'elle fera aller le vaisseau plus viste dans cette route; donc il s'est trompé, et c'est d'icy que j'ay commencè a m'en appercevoir. Toute l'erreur vient de celuy de pag. 18’ (c'est-à-dire de celle signalée par Huygens au commencement de la présente pièce comme se trouvant dans l'Article I du 2 Chapître).
Il semble donc que Huygens était en possession de la règle qui va suivre avant de commencer la lecture suivie du livre du Renaud, dont il pouvait contrôler les résultats au moyen de cette règle.
Remarquons encore qu'on doit lire un peu plus haut dans le texte 38^o 23′ au lieu de 39^o 23′. En effet, la règle qui suit donne x=sin ABC (voir la figure du texte)=0,6210, c'est-à-dire. ∠ ABC=38^o 23′, pour p=sin ABC=sin60^o. Sans dute on a affaire avec une faute d'impression ou de transcription. Dans les manuscrits nous n'avons pas rencontré le calcul en question.

9) Voir pour la déduction de cette règle l'Appendice N^o. 2827.

[p. 529]

sçavoir si x signifie le sinus OQ de l'angle de la voile & du vent, a le Rayon BA, p le sinus FP de l'angle de la quille & du vent. Et elle s'accorde avec celle que Mr. Fatio a trouvée ci-devant, avec beaucoup d'autres belles choses en cette matiere; comme j'ai reconnu par une Table où il avoit marqué le raport de quelques-uns de ces angles¹⁰⁾. Il y a deux vraies racines à cette Equation¹¹⁾, qui servent aux deux cas que la quille avec la ligne du vent fait un même angle: sçavoir en allant près du vent, ou vent largue¹²⁾. Au reste Mr. Renaud ne pourra guere douter que nôtre Regle ne soit vraie, puisque par elle on trouve le meilleur angle du Gouvernail avec la quille pour faire tourner le vaisseau le plus promptement, tout à fait tel qu'il l'a determiné dans le Chapitre 7. En quoi il a fait une découverte fort utile. Car en prenant p=a, c'est-à-dire en faisant la ligne du vent perpendiculaire sur la quille, on trouve par cette regle le sinus x=√⅔aa,

10) Nous ne connaissons pas l'ouvrage ou le manuscrit de Fatio de Duillier qui contenait cette table; mais on retrouve la table elle-même sur une des dernières pages du livre II, sous la forme suivante:

	de la vergue avec la quille.	du vent avec la quille.
	1o	3o.0′
de mr. Fatio.	15o	43o.11⅓′
	40o	109o.12⅔′
	65o	141o.52½′
	90o	180o.0

A a même page le second exemple de la table est vérifié au moyen de la formule p=3x√aa-xx/4aa-3xx qui se déduit aisément de la règle mentionnée et où l'on a dans ce cas, pour a=1, x=sin (43^o 11⅓′-15^o)=sin 28^o 11⅓ et p=sin43^o 11⅓′.
Ajoutons que l'ouvrage en question doit avoir contenu, entre autres, la déduction de la proportion √a³: qui existe entre la vitesse du vaisseau vent arrière et celle avec laquelle il avance avec une situation donnée de la voile et de la quille, car Huygens a annoté à propos de cette proportion, à la page 190 du livre H: ‘Fatio celeritatum’. Voir encore la note 3 de la pièce N^o. 2827.

11) Ce qui est vrai en effet tant qu'on a p < a, comme le problème l'exige. En réalité, les racines de l'équation, considérée comme une équation quadratique en x², sont imaginaires entre les limites p²=a² et p²=9a², et réelles et positives au dehors de ces limites pour p².

12) A vrai dire les angles sont supplémentaires, mais cela ne change pas la valeur de p. L'interprétation donnée par Huygens aux deux racines, de laquelle nous n'avons pas rencontré dans les manuscrits une justification plus précise, est donc correcte. Plus tard, dans l'ouvrage: ‘Essay d'une Nouvelle Theorie de la Manoeuvre des Vaisseaux, Avec quelques Lettres sur le même sujet; par Jean Bernoulli, Profess. de Mathem. & Membre des Académies Royale des Sciences de France, d'Angleterre & de Prusse. A Basle, chez Jean George König, mdccxiv, in-8^o, Jean Bernoulli a repris la question, démontrant, pp. 39-41, que la moindre des racines s'applique au cas du vent étroit et la plus grande au cas du vent large.

[p. 530]

de même qu'il trouve le Sinus de l'angle que la quille, ou la ligne du mouvement de l'eau, fait avec le gouvernail: ce qui doit être ainsi, comme il est aisé de voir¹³⁾.

Quoique toute cette Theorie devienne plus difficile, après la reforme que j'ai indiquée, qu'elle n'étoit au Traité de Mr. Renaud, je vois toutefois qu'il y auroit moyen de determiner par Regle la position du vaisseau & de la voile la plus avantageuse pour gagner au vent, mais la longueur du calcul ne me le permet pas presentement¹⁴⁾; outre que la consideration de la derive du vaisseau n'y seroit

13) En effet, dans ce Chapître 7, qu'il intitule: ‘De l'angle que le gouvernail doit faire avec la



quille du vaisseau, pour prendre vent devant, ou pour arriver vent arriere le plus promptement possible’, Renau se propose de déterminer la position DB du gouvernail pour laquelle la composante de la résistance de l'eau dans la direction BE, perpendiculaire à la direction de la quille BA, devient maximale.
Puisque la résistance de l'eau, dirigée suivant BG est proportionelle, d'après ses principes, au carré du sinus de l'angle d'incidence, qu'on peut représenter par la ligne GH, il est clair, qu'il s'agit de rendre maximale l'expression GH² × BH, c'est-à-dire, posant avec Renaud BH=x, l'expression x (aa-xx); ce qui amène x=BH=√⅓aa, GH=√⅔aa.
Or, évidemment, ce problème est identique au fond avec celui de trouver la meilleure position de la voile DB dans le cas où AB représente la direction du vent et BE celle de la quille du vaisseau, auquel cas GH s'identifie avec le sinus de l'angle de la voile et du vent. c'est-à-dire, avec le x du texte.

14) A la page 190 du livre H on rencontre à cet esset quelques calculs préliminaires. Comme on le verra dans la pièce N^o. 2827, la composante, dans la direction de la quille, de la pression du vent se trouve être proportionnelle à l'expression (bxx-ax³):c (consultez, pour les notations, la note 2 de la pièce N^o. 2827). Par conséquent, la vitesse du vaisseau est proportionnelle à la racine carrée de cette expression; mais, puisqu'il s'agit de la vitesse avec laquelle le vaisseau gagne sur le vent, on doit encore multiplier cette racine par le cosinus de l'angle CBA (voir la sigure de la pièce N^o. 2827), c'est-à-dire par a:c. C'est donc en somme l'expression :c√c qui doit être rendue maximale, ou si l'on veut, puisque a est une constante, l'expression , où p=SN=ab:c.
Huygens la représente par le signe Ω, après quoi il poursuit: ‘invento xx et x ex regula Π pag. 188 [voir la pièce N^o. 2827, vers la sin], per datas a, b, c, siat tabula quae, ad singulas c seu secantes anguli quem facit linea venti cum carina, ostendat sinum x, anguli optimi carinae et veli. Et ex his singulis computato spatio ex formula Ω, notetur quodnam fiet maximum. Sic habebitur et navis et veli positio utilissima, ad insurgendum contra ventum, quod dicunt gagner au vent’.
‘Vel brevius possumus ex singulis hypothesibus sinus veli et venti, invenire sinus venti et carinae, ex regula ♄ pag. 188 [voir toujours la pièce N^o. 2827], ponendo x cognitam, p quaesitam; quae regula ex priore Π sormata est; tum ut sinus complementi anguli cujus sinus p, qui sin. compl. dicatur n, ad rad. a, ita hic ad secantem aa:n=c. Tum ex a, c, b vel p et x computetur longitudo seu spatium Ω. Et siat tabula, ubi apparebit quaenam Ω sit maxima’.
Ajoutons que Jean Bernoulli, dans l'ouvrage cité dans la note 12, a démontré (pp. 43-47) que la condition de maximum de Ω exige p=⅓a√6, x=⅓a√3, c'est-à-dire:CBA=54^o44′, DBA=35^o16′. En effet, si l'on représente ces angles par ψ et par φ, il ne s'agit que de rendre maximale l'expression cos ψ cos φ√sin(ψ-φ) pour les variables indépendantes φ et ψ; ce qui ne présente aucune difficulté avec les méthodes modernes. Huygens lui-même avait d'ailleurs essayé sur une feuille séparée que nous possédons, d'appliquer la méthode de la pièce N^o. 2827 à l'expression Ω en y substituant pour p la valeur indiquée par la formule ♄ de cette pièce et pour c celle calculée au moyen de cette formule et de la relation p²=a²b²:c²=a²(c²-a²):c²; mais il n'avait pu mener ces calculs à bonne sin. Enfin, une annotation qu'on trouve à la page 79 du Livre J semble indiquer que Huygens a cherché plus tard à déterminer, par voie expérimentale, les positions les plus avantageuses de la voile et de la quille, puisqu'on y lit ‘trouvé mechaniquement que la plus avantageuse disposition de la quille et de la voile pour gagner au vent, est environ quand l'angle du vent et de la quille est de 60 degr. et l'angle du vent et de la voile de 38 degr.’.

[p. 531]

pas comprise, qui aporte beaucoup de difficulté; parce qu'il est necessaire d'avoir égard non seulement au plus de facilité que le vaisseau a en fendant l'eau avec sa pointe qu'avec le côté, ainsi qu'a fait l'Auteur, mais encore à l'impulsion differente que reçoit le corps du vaisseau par le vent, sur tout par les côtez, ce qui fait qu'une seule experience ne pourroit pas suffire pour servir de fondement dans le reste, en ce qui est de la derive¹⁵⁾.

15) A propos de ce dernier passage Jean Bernoulli, dans l'écrit cité, fait remarquer, pp. 102-103, que même en faisant abstraction de l'impulsion du vent sur le corps du vaisseau la dérive dans les différentes positions du vaisseau n'est pas déterminée par la proportion seule des résistances de l'eau contre le côté du vaisseau et contre la pointe, mais que la figure du vaisseau doit entrer en considération.