Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–No 2825.
| |||
[pagina 519]
| |||
Solution. Lorsque la raison de p à q est de nombre à nombre, ayant nommé les indeterminées CP, y, PM, x; on se servira de ces formules generales:
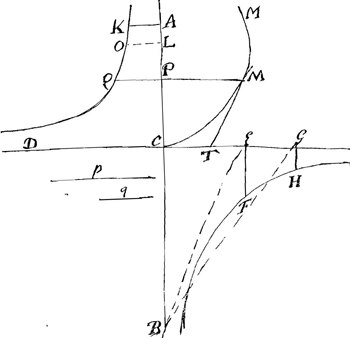 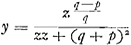 , ou bien , ou bien 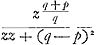 et x=zzy+qqy-ppy/2pz, et ayant fait evanouir l'inconnuë z on formera deux equations qui exprimeront chacune la nature d'une ligne courbe CMM qui satisfait à la questionGa naar voetnoot2). Supposant par exemple que p soit double de q, on trouvera y=a4/zz+9aazGa naar voetnoot3) ou z3/zz+aa et x=zzy-3aay/4az, d'où l'on tire ces deux equations: 432y4+432xxyy+ et x=zzy+qqy-ppy/2pz, et ayant fait evanouir l'inconnuë z on formera deux equations qui exprimeront chacune la nature d'une ligne courbe CMM qui satisfait à la questionGa naar voetnoot2). Supposant par exemple que p soit double de q, on trouvera y=a4/zz+9aazGa naar voetnoot3) ou z3/zz+aa et x=zzy-3aay/4az, d'où l'on tire ces deux equations: 432y4+432xxyy+
| |||
[pagina 520]
| |||
+72axyy+64ax3=aayy et 16y4+16xxyy-72axyy-64ax3=27aayyGa naar voetnoot4), qui expriment chacune la nature d'une ligne courbe CMM, dont les touchantes MT sont doubles des parties CT de l'axe faites par leur rencontres. Jl en est ainsi des autres. Lorsque la raison n'est pas de nombre à nombre; ayant tiré les droites indefinies AB, DE, qui s'entrecoupent à angles droits au point C, on decrira entre les asymptotes CA, CD, une hyperbole quelconque KOQ, et menant librement AK parallele à CD qui rencontre l'hyperbole en K, et EF parallele à CB telle, que le rectangle CEF soit au rectangle CAK, comme la difference des deux lignes p et q est à la ligne q: on decrira par le point F entre les asymptotes CB, CE une autre hyperbole FH; on menera ensuite librement GH parallele à CB, et prenant CB egale à p+q, on fera comme le quarré de BG est au quarré de BE, de mesme CA est à CL, par ou l'on tirera LO parallele à CD. On prendra enfin l'espace hyperbolique LPQO (du mesme côté de l'espace ALOK par rapport à CD, lorsque p surpasse q, et du côté opposé lorsqu'il est moindre) égal à l'espace hyperbolique EGHFGa naar voetnoot5) et nommant CP, y, CG, z, on prolongera PQ en M, de sorte que PM=zzy+qqy-ppy/2pz, je dis que le point M sera à la courbe cherchée CMM. Ou bien. Ayant tiré les droites indéfinies AB, DE qui s'entre coupent à angles droits au point C, on décrira entre les asymptotes CA, CD une hyperbole quelconque KOQ, et menant librement AK parallele à CD, qui rencontre l'hyperbole au point K, et EF parallele à CB telle, que le rectangle CEF soit au rectangle CAK comme p+q est à q: on decrira par le point F entre les asymptotes CB, CE une autre hyperbole FH: On menera ensuite librement GH parallele a CB, et prenant CB egale à la difference des deux lignes p et q, on fera comme le | |||
[pagina 521]
| |||
quarré de BG est au quarré de BE, de mesme CA est à CL, par où l'on tirera LO parallele à CD: on prendra ensin l'espace hyperbolique LPQO (du coté opposé à celui de l'espace ALOK par rapport à CD) egal à l'espace hyperbolique EGHFGa naar voetnoot5), et nommant CP, y, CG, z, on prolongera PQ en M de sorte que PM=zzy+qqy-ppy/2pz. Je dis que le point M sera à une ligne courbe CMM, qui resout encore le probleme. Voici ce que me mandoit Mr. Bernoulli. ‘1o. Je trouve vostre construction bien prolixe et embarassée; la mienne est bien plus aisée et ne demande pas qu'on prenne deux espaces hyperboliques égaux. 2o. Je ne scais pas pourquoi vous trouvez toujours deux courbes qui satisfassent à la question en quelle raison que soit p à q, il me semble pouvoir demontrer qu'il n'y en a qu'une qui reponde au probleme. 3o. Vous dites que si la raison de p à q est comme 2 à 1, les deux courbes seront 432y4+432xxyy+72axyy+64ax3=aayy, et 16y4+16xxyy-72axyy-64ax3=27aayy; mais par ma solution generale, je trouve dans ce cas cette equation y4+xxyy+18axyy+16ax3=27aayy, qui n'est pas semblable ni à l'une ni l'autre des vôtres; et ce qu'il y a de plus, c'est que si vous cherchez reciproquement la tangente MT et la partie CT de vos deux courbes, vous trouverez que MT est à CT non comme 2 à 1, ce qui est une preuve invincible qu'il y a ici une saute. 4o. Vous ne disconvenez pas que la courbe CMM ne soit un cercle lorsque p à q ou MT à CT est une raison d'egalité, or au lieu qu'il n'y a que le cercle (comme il est manifeste au plus petit geometre) qui puisse satisfaire, vous trouvez deux lignes differentes, dont ni l'une ni l'autre est un cercle; car votre premiere formule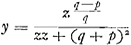 donne une ellipse, et la seconde donne une ellipse, et la seconde 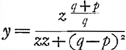 ne produit qu'une ligne droite parallele à CD. Ce dernier argument est tout seul suffisant pour vous donner la peine de repasser le calcul et de chercher la faute, quand vous l'aurez trouvée, vous me pouvez envoyer la correction, il sera alors assez temps d'envoyer vôtre solution a LeipsicGa naar voetnoot6), qui sera encore des premieres apres celle de mon frereGa naar voetnoot7) et la mienne’Ga naar voetnoot8). ne produit qu'une ligne droite parallele à CD. Ce dernier argument est tout seul suffisant pour vous donner la peine de repasser le calcul et de chercher la faute, quand vous l'aurez trouvée, vous me pouvez envoyer la correction, il sera alors assez temps d'envoyer vôtre solution a LeipsicGa naar voetnoot6), qui sera encore des premieres apres celle de mon frereGa naar voetnoot7) et la mienne’Ga naar voetnoot8).
J'y ai repondu par articles en cette sorte: ‘1o. Si l'on proposoit de décrire une | |||
[pagina 522]
| |||
courbe dont la soutangente fust toujours à l'abcisse en raison constante; il est clair ce me semble que la construction la plus simple et la plus generale demanderoit qu'on prist deux espaces hyperboliques egaux, et toutefois cette courbe est bien moins composée que la vôtre. 2o. Je soutiens qu'il y a toujours deux courbes qui satisfont egalement qui sont celles que l'on trouve par mes deux constructions et de plus qu'il n'y en peut avoir d'autres. 3o. Votre courbe y4+xxyy+18axyy++16ax3=27aayy, est la mesme que ma seconde 16y4 &c.; car si l'on suppose a=4b et qu'on divise par 16, on trouve y4+xxyy-18bxyy-16bx3=27bbyy, qui ne differe de la vôtre qu'en ce que les valeurs des appliquées x sont changées de fausses en vrayes et au contraire, ce qui ne change rien dans la courbe que sa position. Mais asin qu'il ne vous reste aucun scrupule sur ma premiere equation, et que vous en puissiez faire aisement le calcul, supposez a=12b, et divisez chaque terme par 48, ce qui vous donnera 9y4+9xxyy+18bxyy+16bx3==bbyy, et vous trouverez que cette courbe (si vous en faites le calcul) a ses tangentes MT doubles des parties CT de l'axe. D'ou il est evident que ma construction est conforme à la vôtre en ce cas, et qu'elle est beaucoup plus generale, puisqu'elle donne toujours deux lignes courbes ou vous n'en trouvez qu'une. 4o. Ma premiere
formule donne xx+yy=1 4ppGa naar voetnoot9), qui est une equation à un cercle qui a pour rayon 1/2p, et ma seconde donne à la verité une ligne droite parallele à CD
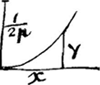 mais elle satisfait aussi dans ce cas comme il est manifeste au plus petit geometre; car si l'on mene d'un de ses points quelconques M une tangente MT, elle sera la droite mesme et n'ira rencontrer l'axe CD qu'à une distance infinie; d'où il suit que ces deux lignes MT, CT seront egales entr'elles, puis qu'elles ne different que de la quantité PM, qui est finie’. Vous voyez, Monsieur, que la construction de Mr. Jac. Bernouilli, est moins generale que la mienne. Mais il me semble de plus qu'on parvient plus difficilement à l'equation qui exprime la nature de la courbe; car si l'on nomme AB, xGa naar voetnoot10); BC, y; DC, z; on trouve selon lui ces formules yGa naar voetnoot11)=((n+1)z+(n-1)z2n+1/1+z2n) et zz=yy+xx-2nxz+nnzz, qui me paroissent moins simples que les miennes. Lorsque la raison ne s'exprime que par des lignes, il faut du moins pour avoir la | |||
[pagina 523]
| |||
valeur de DB employer la quadrature de l'hyperbole ou les logarithmes, et il ne donne alors aucune construction; de sorte que ce n'est pas merveille s'il ne suppose point qu'on prenne des espaces hyperboliques egaux. Voici en abregé mon analyse: CP=y, PM=x, donc MT=y√(dx2+dy2)/dy et CT=xdy-ydx/dy et par la condition du probleme y√dx2+dy2:xdy-ydx∷p:q, d'ou je tire, (en supposant pour abbreger pp-qq=mm) dx2-2ppxdydx/mmy==qqyydy2-ppxxdy2/mmyy et la resolution de cette egalité, (dont je regarde dx comme l'inconnue) me donne mmydx=ppxdy ∓ qdy√mmyy+ppxx, que je change en cette autre equation: dy/y=mmdu/qq ∓ q√ppuu+mmGa naar voetnoot12) (en mettant pour x, uy; et pour dx, udy+ydu) par le moyen de laquelle je pourois deia construire la courbe. Mais je suppose pour oster les incommensurables √ppuu+mm=z--pu, et partant u=zz-mm/2pz et du=zzdz+mmdz/2pzz. Ces valeurs me donnent par la substitution:
qui m'ont servi à former mes deux constructions. Comme vous avez trouvé l'analyse de Mr. Bernoulli je ne la chercherai point et je l'attens de vous. Au reste ma seconde suitte donne les memes quadratures que celle de Mr. Gregori. Vous le reconnoistrez aisement pour peu que vous vous y appliquiez. Mais il faut dans l'une et l'autre retrancher toujours ma 3o. suite, ce que Mr. Gregori devoit remarquer, car autrement je puis demontrer que ses quadratures seroient fausses. L'autheur du livre de la manoeuvre de vaisseaux est Mr. RenaudGa naar voetnoot13), que je connois particulierement et qui a la charge d'ingenieur de | |||
[pagina 524]
| |||
la marine. Vous me ferez plaisir de me mander ce que vous en pensez. J'acheverai de repondre à ce que vous souhaitez de moi dans ma 1ere. lettreGa naar voetnoot14). Je vous prie de ne pas oublier de m'envoyer les inventions de Mr. NeutonGa naar voetnoot15) lorsque vous les aurez receues et je serois bien aise aussi de savoir les manieres dont vous decrivez la courbe de Mr. Bernoulli, que vous me mandez estre meilleures que la sienne. Je suis Monsieur avec beaucoup de zele vôtre tres humble et tres obeissant serviteur le M. de l'Hospital. Apres ma lettre écritte je n'ay pu m'empescher de chercher la maniere dont Mr. Bernoulli pouvoit avoir trouvé sa construction, et j'y suis arrivé par un chemin assez court que voici. Soit DC=z, DB=x donc AD=nz, AB=nz+x, et leur differentielles Dd=ndz, Bb ou CE=dx+ndz. Or à cause des triangles semblables DBC, CEe et DFd, ou aura DB:DC∷CE:Ce=zdx+nzdz/x et 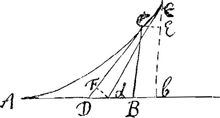 DC:DB∷Dd:DF=nxdz/z c'est-dire à la differentielle Cc de la courbe moinsGa naar voetnoot16) la differentielle de la touchante DC; d'ou l'on tire nxxdz++xzdz=zzdx+nzzdz, et faisant x=uz il vient dz/z=du/nuu-n qui est apparemment l'equation, où vous estes arrivé, et dont on déduit facilement le reste. Si vous avez suivi une autre voye vous me ferez plaisir de m'en faire part. |
|