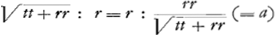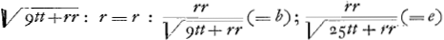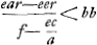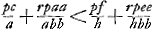No 2835.
Christiaan Huygens.
[Août ou septembre 1693].
Appendice IIGa naar voetnoot1) au No. 2833.
La pièce se trouve à Leiden, coll. Huygens.
Quaeritur an eadem sit Catenaria atque ea quae a tenso velo, quod ita esse Bernoulij dicunt, quos decipi video. (Voiez le 16e Journal des Scavans de 1692, mois d'avril, ou Mr. Bernouli le frère du Prof. assure qu'il a trouvè que la Courbure de la voile est la mesme que celle de la ChaineGa naar voetnoot2), sans y apporter ces distinctions que le Prof.r remarque dans les Acta du mois de may 1692Ga naar voetnoot3). Voiez aussi les Acta de 1691, mois de Juin, où Jac. Bernoulli se trompe desiaGa naar voetnoot4).
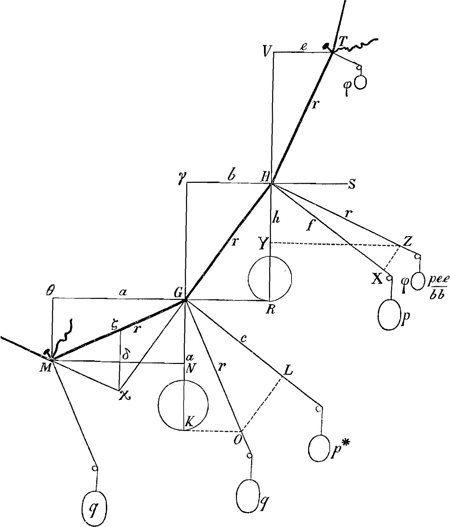
Partes veli aequales MG, GH, HT, ponuntur hic eo situ quem haberent ejusmodi partes aequales in Catena pendente; deinde quaeritur an vento velum istud inflante, mansurae sint partes ita positae. Inveniturque punctum H nonnihil depressum iri, eoque G ascenturum. (Hinc quidem sequitur velum ex rectangulis aequalibus alicujus magnitudinis constans, non mansurum eo positu quo catena ex talibus rectangulis composita: sed posset in infinite parvis, infiniteque multis, evanescere exigua ista diversitas. Nondum etiam clare sequitur, ut quia H punctum in velo deprimitur, ideo obtusior esse debeat velaria in vertice quam Catenaria.
| |
Tangentes angulorum GMN, HGR, THS, sunt ut 1, 3, 5 cum pondera aequalia R et K, et ζδ=δχGa naar voetnoot6).
Vis venti in aequales MG, GH, HT spirantis secundum θM, est ac si perpendiculariter in medio premerentur viribus quae sunt ut quadrata θG, γH, VT. Pro quibus bina pondera aequalia, singulas MG, GH, HT perpendiculariter trahentia, substituo, qualia sunt p, p trahentia GH; q, q trahentia MG, sed quorum alterum duntaxat quod in G trahit considerandum; φφ trahentia HT, quorum alterum duntaxat considerandum quod trahit in H.
Jam pro q et p* trahentibus in G quaero aequivalentiaGa naar voetnoot7) duo quae traherent per GK. Itemque pro p et φ trahentibus in H quaero aequivalentia duo quae traherent per HR; quae si dictis duobus per GK trahentibus aequalem summam efficiunt, sequitur pressionem venti et catenae pondus eandem curvam efficere. Sed hic praevalere invenio trahentia per HR.
a (GK):c (GL)=p:pc/a, pondus trahens per GK aequivalens ponderi trahenti per LGGa naar voetnoot8).
bb:aa=p:paa/bb (=q); a (GK):r(GO)=paa/bb(q):rpaa/abb, pondus trahens per KG aequipollens ponderi paa/bb trahenti per GO.
h [HY]:f [HX]=p:pf/h [pondus trahens per HR aequipollens ponderi p trahenti per HX].
bb:ee=p:pee/bb[=φ]; h [HY]:r [HZ]=pee/bb[φ]:rpee/hbb [pondus trahens per HR aequipollens ponderi φ trahenti per HZ].
| |
Ut nihil contra hanc refutationem per numeros sinuum excipi possit, omnes quantitates, cum ad summam inferiorum officiendam adhibentur, pauli majores veris sumantur in numeratoribus, minores in denomin. Cum vero ad summum superiorum ponderum adhibentur sumantur paulo veris minores, id est, minores in numeratoribus, majores in denominatoribus, sed r est verus radius=100000Ga naar voetnoot15). |
-
voetnoot1)
- Cet Appendice, emprunté aux pages 72 et 73 du livre J, contient la démonstration ‘qu'une voile faite de certain nombre de rectangles égaux et inflexibles estant étendue par le vent’ ne pourra prendre la même position qu'une telle chaîne le ferait par son poids. On y suppose, conformément aux principes mentionnés dans la note 4 de la Lettre No. 2826, que la pression du vent dans la direction perpendiculaire aux parallélogrammes MG, GH, HT, etc., est proportionelle aux carrés de leurs projections sur le plan perpendiculaire à la direction du vent, c'est-à-dire, dans le cas de la figure, proportionelle aux θG2, γH2, VT2, etc.
-
voetnoot2)
- Voir l'article cité dans la note 2 de la Lettre No. 2801. Dans cet article Jean Bernoulli assure qu'il avait non seulement retrouvé la méthode par laquelle son frère était arrivé à l'équation différentielle ads ddx=dy3 de la voilière (voir la note 20 de la Lettre No. 2829), mais qu'il avait résolu tout le problème et trouvé ‘que la courbe de la voile est la même que celle d'une chaîne’; quand on le voudrait il donnerait la manière analytique qui l'avait conduit à la connaissance de cette courbe.
-
voetnoot3)
- Il s'agit de l'article cité dans la Lettre No. 2819, note 25. Jacques Bernoulli y identifie la courbe de la voile avec celle de la chaînette, sauf la restriction que nous avons indiquée dans la note 33 de la Lettre No. 2693 et qui regarde la partie BC de la voile représentée dans la figure de la note citée.
-
voetnoot5)
- Probablement les phrases que nous avons mises entre parenthèses ont-elles été ajoutées plus tard.
-
voetnoot6)
- Consultez, à propos de cette assertion, le § I de la pièce No. 2625. Pour appliquer à la figure du texte le théorème qu'on y trouve en italiques à la tête de ce paragraphe, on doit remarquer que Huygens suppose que le point M est le point le plus bas de la chaîne, de telle manière que l'interstice qui va suivre à gauche de ce point possède une inclinaison égale (mais contraire) à celle de l'interstice MG. De cette manière la suite des nombres proportionnels aux tangentes des angles que font les interstices avec l'horizon, doit s'écrire (en commençant par l'interstice à gauche de M):-1, 1, 3, 5, etc.
-
voetnoot7)
- C'est-à-dire équivalent quant au travail virtuel pour un petit déplacement compatible avec les liaisons. Voir les calculs qui vont suivre.
-
voetnoot8)
- Ces deux forces, en effet, pour produire le même travail virtuel, devront être inversement proportionnelles aux projections du déplacement virtuel sur leurs directions, et ce déplacement, le point M restant fixe, sera dirigé selon GO.
-
voetnoot9)
- C'est donc ici la condition nécessaire et suffisante pour que la situation de la voile obtenue sous l'influence de deux poids égaux en G et en H, puisse se conserver sous la pression du vent. Dès lors il ne s'agit plus que de simplifier cette condition et de l'éprouver par le calcul d'un cas particulier.
-
voetnoot10)
- Parce que les longueurs arbitraires GO et HZ ont été égalées par Huygens aux interstices MG, GH, etc.
-
voetnoot11)
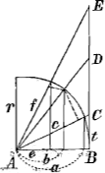
- Voir la fig. 2, où les droites AE, AD, AC représentent les directions des interstices successives MG, GH, HT de la fig. 1. On a donc, pour BC=t, BD=3t, EB=5t, et si l'on prend pour t une valeur arbitraire, comme 30001 (le rayon étant 100000), il est facile de trouver les angles et les lignes de la figure et d'en déduire, comme il va suivre, les valeurs de a, b, e, f et c.
-
voetnoot13)
- Nous supprimons ici et dans la suite quelques calculs numériques.
-
voetnoot14)
- Puisque l'inégalité constatée entraîne
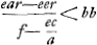
; donc aussi, remontant les calculs de la page précédente:
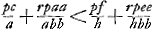
.
-
voetnoot14)
- Puisque l'inégalité constatée entraîne ear-eer/f-ec/a<bb; donc aussi, remontant les calculs de la page précédente: pc/a+rpaa/abb<pf/h+rpee/hbb.
-
voetnoot15)
- La pièce est suivie dans le livre J par un ‘alius facilior calculus’ et un ‘tertius facilior calculus’ qui se distinguent du calcul que nous avons reproduit par une autre situation des trois interstices. Dans le ‘alius facilior’ les deux premiers interstices ont des inclinaisons égales mais contraires par rapport à l'horizon, dans l'autre le premier interstice est horizontal, à propos duquel Huygens remarque encore: ‘Hinc facillime ulterius calculum prosequi possem ad ulteriores catenae partes’; ce que, toutefois, il n'a pas exécuté.
Tous ces calculs mènent a la conclusion que, pour ‘équivaler’ aux pressions du vent contre les interstices, le poids inférieur devra être moins lourd que le poids supérieur. En étendant cette conclusion à toute la chaîne, on est donc conduit à supposer que la courbe de la voile sera moins pointue que la chaînette correspondante, puisque la partie inférieure, près du sommet M, y est allégée par rapport à la partie supérieure, ou, comme Huygens l'exprime ‘Ergo rotundior est figura veli quam catenae, magisque a figura parabolica recedit. Falluntur ergo Bernoulij’. En effet, dans le cas de la parabole, comme chaînette, les petits interstices égaux devront être chargés par des poids proportionels à leurs projections horizontales (voir la Propositio 12 de la pièce No. 21), c'est-à-dire, les poids inférieurs y surpasseront tout au contraire les poids supérieurs.
Reste donc la question de savoir si l'effet constaté par Huygens ne s'amoindrira pas de plus en plus avec le nombre croissant des interstices, jusqu'à disparaître quand ce nombre devient infini. C'est, en effet, ce qui a lieu. Et pour le constater il suffira de calculer la différence des deux poids successifs qui équivalent ensemble à la pression du vent dans le cas de trois interstices consécutifs de longueur Δs, faisant des angles α, β et γ avec le plan perpendiculaire à la direction du vent, que nous identifions avec le plan horizontal.
Dans ce calcul nous supposerons d'abord, afin de mieux faire saisir la portée du raisonnement qui va suivre, que la pression du vent soit une fonction arbitraire f (α) de l'angle α de l'interstice avec le plan horizontal. Dans cette supposition on trouve pour le poids inférieur: ½f(α)(cosα)-1+½f(β)cos(β-α)(cosα)-1 et pour le poids supérieur: ½f(γ) (cosγ)-1++½f(β).cos(γ-β).(cosγ)-1. Posant alors, comme il est permis en première approximation, β=α+ε, γ=α+2ε, où ε=Δs. ϱ-1 représente l'angle de contingence de la voilière et ϱ le rayon de courbure, la différence des deux poids sera représentée, toujours en première approximation, par l'expression: [2f(α). sin α.(cos α)-2+f′ (α).(cos α)-1].Δs. ϱ-1.
Cette différence est donc, généralement parlant, du premier ordre par rapport à la longueur des interstices; mais dans le cas où l'on suppose (avec Huygens et les Bernoulli) f(α)==kcos2 α et dans ce cas seulement, l'expression entre parenthèses s'évanouit et la différence des poids équivalents devient du second ordre par rapport à Δ s, c'est-à-dire elle va disparaître tout le long de la courbe au moment que le nombre des interstices devient infini.
De cette manière la méthode de Huygens nous fournit une nouvelle démonstration, assez élégante, de l'identité de la voilière des Bernoulli avec la chaînette ordinaire.
|